Đề bài
Cho đường tròn \((O;4cm)\) và một điểm \(M\) sao cho \(OM = 8cm.\) Kẻ tiếp tuyến \(MN\) với đường tròn \((O), N\) là tiếp điểm (h.124). Số đo của góc \(MON\) là:
(A) \(45^o;\) (B) \(90^o;\)
(C) \(30^o;\) (D) \(60^o.\)
Hãy chọn đáp số đúng.
Phương pháp giải - Xem chi tiết
Sử dụng:
- Trong tam giác vuông các tỉ số lượng giác của góc nhọn \((\alpha)\) được định nghĩa như sau:

\(\sin \alpha = \dfrac{{AB}}{{BC}};\cos \alpha = \dfrac{{AC}}{{BC}};\)\(\tan \alpha = \dfrac{{AB}}{{AC}};\cot \alpha = \dfrac{{AC}}{{AB}}.\)
Lời giải chi tiết
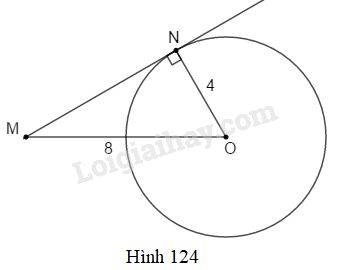
Xét \(\Delta OMN\) vuông tại \(N\) ta có:
\(\begin{array}{l}
\cos \widehat {MON} = \dfrac{{ON}}{{OM}} = \dfrac{1}{2}\\
\Rightarrow \widehat {MON} = {60^o}
\end{array}\)
Chọn D.
dapandethi.vn
