Đề bài
Tính sin, cos, tang của các góc \(A \) và \(B\) của tam giác \(ABC\) vuông ở \(C\) biết:
a) \(BC= 8, AB = 17;\)
b) \(BC=21,AC=20;\)
c) \(BC=1,AC=2;\)
d) \(AC=24,AB=25.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
- Định lí Pytago: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
- Trong tam giác vuông các tỉ số lượng giác của góc nhọn \((\alpha)\) được định nghĩa như sau:

\(\sin \alpha = \dfrac{{AB}}{{BC}};\cos \alpha = \dfrac{{AC}}{{BC}};\)\(\tan \alpha = \dfrac{{AB}}{{AC}};\cot \alpha = \dfrac{{AC}}{{AB}}.\)
Lời giải chi tiết
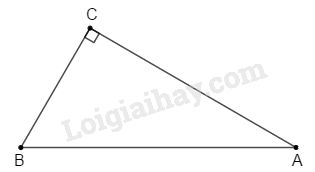
a) Áp dụng định lí Pytago vào tam giác \(ABC\) vuông tại \(C\), ta có:
\(A{B^2} = B{C^2} + A{C^2}\)
\(\Rightarrow AC = \sqrt {A{B^2} - B{C^2}} = \sqrt {{{17}^2} - {8^2}} \)\(\,= 15\)
Tam giác \(ABC\) vuông tại \(C\) nên \(\widehat A\) và \(\widehat B\) là hai góc phụ nhau, ta có:
\(\begin{array}{l}
\sin A = \cos B = \dfrac{{BC}}{{AB}} = \dfrac{8}{{17}}\\
\cos A = \sin B = \dfrac{{CA}}{{AB}} = \dfrac{{15}}{{17}}\\
\tan A = \cot B = \dfrac{{BC}}{{AC}} = \dfrac{8}{{15}}\\
\cot A = \tan B = \dfrac{{AC}}{{BC}} = \dfrac{{15}}{8}
\end{array}\)
b) Áp dụng định lí Pytago vào tam giác \(ABC\) vuông tại \(C\), ta có:
\(A{B^2} = B{C^2} + A{C^2} = {21^2} + {20^2}\)\(\, = 841\)
\(\Rightarrow AB = \sqrt {841} = 29\).
Tam giác \(ABC\) vuông tại \(C\) nên \(\widehat A\) và \(\widehat B\) là hai góc phụ nhau, ta có:
\(\begin{array}{l}
\sin A = \cos B = \dfrac{{BC}}{{AB}} = \dfrac{{21}}{{29}}\\
\cos A = \sin B = \dfrac{{AC}}{{AB}} = \dfrac{{20}}{{29}}\\
\tan A = \cot B = \dfrac{{BC}}{{AC}} = \dfrac{{21}}{{20}}\\
\cot A = \tan B = \dfrac{{AC}}{{BC}} = \dfrac{{20}}{{21}}
\end{array}\)
c) Áp dụng định lí Pytago vào tam giác \(ABC\) vuông tại \(C\), ta có:
\(\begin{array}{l}
A{B^2} = B{C^2} + A{C^2} = {1^2} + {2^2} = 5\\
\Rightarrow AB = \sqrt 5
\end{array}\)
Tam giác \(ABC\) vuông tại \(C\) nên \(\widehat A\) và \(\widehat B\) là hai góc phụ nhau, ta có:
\(\begin{array}{l}
\sin A = \cos B = \dfrac{{BC}}{{AB}} = \dfrac{1}{{\sqrt 5 }}\\
\cos A = \sin B = \dfrac{{AC}}{{AB}} = \dfrac{2}{{\sqrt 5 }}\\
\tan A = \cot B = \dfrac{{BC}}{{AC}} = \dfrac{1}{2}\\
\cot A = \tan B = \dfrac{{AC}}{{BC}} = \dfrac{2}{1} = 2
\end{array}\)
d) Áp dụng định lí Pytago vào tam giác \(ABC\) vuông tại \(C\), ta có:
\(A{B^2} = B{C^2} + A{C^2}\)
\( \Rightarrow BC = \sqrt {A{B^2} - A{C^2}} \)\(\,= \sqrt {{{25}^2} - {{24}^2}} \)\(\, = \sqrt {49} = 7\)
Tam giác \(ABC\) vuông tại \(C\) nên \(\widehat A\) và \(\widehat B\) là hai góc phụ nhau, ta có:
\(\begin{array}{l}
\sin A = \cos B = \dfrac{{BC}}{{AB}} = \dfrac{7}{{25}}\\
\cos A = \sin B = \dfrac{{AC}}{{AB}} = \dfrac{{24}}{{25}}\\
\tan A = \cot B = \dfrac{{BC}}{{AC}} = \dfrac{7}{{24}}\\
\cot A = \tan B = \dfrac{{AC}}{{BC}} = \dfrac{{24}}{7}
\end{array}\)
dapandethi.vn
