Đề bài
Cho tam giác ABC vuông tại A có \(\widehat C = {60^0}\) . Kẻ AH vuông goác với BC tại H, trên tia đối của tia AH lấy điểm D sao cho HD = HA.
a) Chứng minh rằng \(\Delta ABD\) đều.
b) Từ D kẻ đường thẳng song song với AB cắt BC tại M. Chứng minh rằng đều.
Lời giải chi tiết
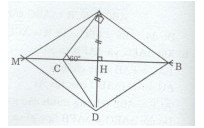
a)Ta có: \(\widehat {ACH} + \widehat {HAC} = {90^0}(\Delta AHC\) vuông tại H)
\(\widehat {HAC} + \widehat {HAB} = {90^0}(\Delta ABC\) vuông tại A)
Suy ra: \(\widehat {ACB} = \widehat {HAB} = {60^0}\)
Mặt khác \(AH \bot BC(gt) \Rightarrow \widehat {AHB} = \widehat {DHB} = \widehat {MHA} = \widehat {MHD} = {90^0}\)
Xét tam giác ABH và DBH có:
AH = DH (giả thiết)
HB là cạnh chung.
\(\widehat {AHB} = \widehat {DHB}({90^0})\)
Do đó: \(\Delta ABH = \Delta DBH(c.g.c)\)
Suy ra: AB = BD => tam giác ABD cân tại B.
Mà \(\widehat {BAD} = {60^0}.\) Do vậy tam giác ABD đều.
b) Ta có: AB // MD (gt)
\(\Rightarrow \widehat {ADM} = \widehat {BAD}\) (hai góc so le trong) nên \(\widehat {ADM} = {60^0}.\)
Xét tam giác MHA và MHD có:
HA = HD (gt)
\(\widehat {MHA} = \widehat {MHD}( = {90^0})\)
MH là cạnh chung.
Do đó: \(\Delta MHA = \Delta MHD(c.g.c) \Rightarrow MA = MD \Rightarrow \Delta ADM\) cân tại M.
Mà \(\widehat {ADM} = {60^0}.\) Vậy tam giác ADM đều.
dapandethi.vn
