Đề bài
Tứ giác \(ABCD\) có \(AB = 4cm, BC = 20 cm\), \(CD = 25 cm, DA = 8cm\), đường chéo \(BD = 10cm\).
a) Nêu cách vẽ tứ giác \(ABCD\) có kích thước đã cho ở trên.
b) Các tam giác \(ABD\) và \(BDC\) có đồng dạng với nhau không? Vì sao?
c) Chứng minh rằng \(AB // CD\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng cách vẽ tam giác, dấu hiệu nhận biết hình thang, dấu hiệu nhận biết hai tam giác đồng dạng.
Lời giải chi tiết
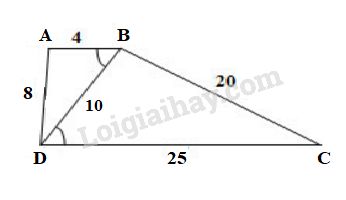
a) Cách vẽ:
- Vẽ \(ΔBDC\):
+ Vẽ \(DC = 25cm\)
+ Vẽ cung tròn tâm \(D\) có bán kính \(10cm\) và cung tròn tâm \(C\) có bán kính \(20cm\). Giao điểm của hai cung tròn là \( B\).
- Vẽ điểm A: Vẽ cung tròn tâm \(B\) có bán kính \( 4cm\) và cung tròn tâm \(D\) có bán kính \( 8cm\). Giao điểm của hai cung tròn này là điểm \(A\). Nối các cạnh BD, BC, DA, BA.
Vậy là ta đã vẽ được tứ giác \(ABCD\) thỏa mãn điều kiện đề bài.
b) Ta có: \(\dfrac{{AB}}{{BD}} = \dfrac{4}{{10}} = \dfrac{2}{5};\) \(\dfrac{{BD}}{{DC}} = \dfrac{{10}}{{25}} = \dfrac{2}{5};\) \(\dfrac{{AD}}{{BC}} = \dfrac{8}{{20}} = \dfrac{2}{5}\)
\( \Rightarrow \dfrac{{AB}}{{BD}} = \dfrac{{BD}}{{DC}} = \dfrac{{AD}}{{BC}}\)
\(\Rightarrow \Delta AB{\rm{D}} \backsim \Delta B{\rm{D}}C\left( {c - c - c} \right)\)
c) \(∆ABD∽ ∆BDC\) (chứng minh trên)
\(\Rightarrow \widehat {ABD} = \widehat {BDC}\), mà hai góc ở vị trí so le trong.
\(\Rightarrow AB // DC\) hay \(ABCD\) là hình thang.
dapandethi.vn
