Đề bài
Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình thoi.
Phương pháp giải - Xem chi tiết
Áp dụng dấu hiệu nhận biết hình thoi: Tứ giác có bốn cạnh bằng nhau là hình thoi.
Lời giải chi tiết
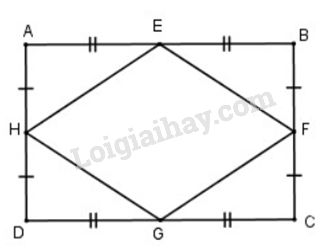
Xét hình chữ nhật \(ABCD\) có \(E,F,G,H\) lần lượt là trung điểm của \(AB,BC,CD,DA\)
Xét \(∆AEH\) và \(∆BEF\) có:
\(AE = BE \) (vì \(E\) là trung điểm \(AB\))
\(\widehat A = \widehat B = {90^0}\)
\(AH = BF\) (vì \(AH = \dfrac{1}{2}AD \); \(BF= \dfrac{1}{2}BC\); \(AD=BC\) )
Do đó \(∆AEH=∆BEF\) (c.g.c), suy ra \(EH = EF \) (2 cạnh tương ứng)
Chứng minh tương tự ta có: \(EF=GF, GF=GH\).
Tứ giác \(EFGH\) có \(EH = EF= GF=GH\) nên là hình thoi (theo định nghĩa).
Chú ý:
Xét \(∆HDG\) và \(∆FCG\) có:
\(H{\rm{D}} = FC\left( {cmt} \right)\) (vì \(HD = \dfrac{1}{2}AD \); \(FC= \dfrac{1}{2}BC\); \(AD=BC\) )
\(\widehat D = \widehat C = {90^0}\)
\(DG = CG\) (vì \(G\) là trung điểm \(DC\))
\( \Rightarrow \Delta HDG = \Delta FCG\left( {c - g - c} \right)\)
\( \Rightarrow \) \(GH = GF \) (2 cạnh tương ứng)
Xét \(∆AHE\) và \(∆DHG\) có:
\(H{\rm{A}} = HD\) (vì \(H\) là trung điểm \(AD\))
\(\widehat A = \widehat D = {90^0}\)
\(AE = DG\) (vì \(AE = \dfrac{1}{2}AB \); \(DG= \dfrac{1}{2}DC\); \(AB=DC\) )
\(\Rightarrow \Delta AHE = \Delta DHG\left( {c - g - c} \right)\)
\( \Rightarrow \) \(EH = GH \) (2 cạnh tương ứng)
\( \Rightarrow HE=EF = GH = GF\).
dapandethi.vn
