Đề bài
Hai đường chéo của một hình thoi bằng \(8cm\) và \(10cm\). Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:
(A) \(6cm\); (B) \(\sqrt {41} cm\)
(C) \(\sqrt {164} cm\) (D) \(9cm\)
Phương pháp giải - Xem chi tiết
Áp dụng:
- Tính chất của hình thoi: Hai đường chéo của hình thoi vuông góc và cắt nhau tại trung điểm mỗi đường;
- Định lí Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết
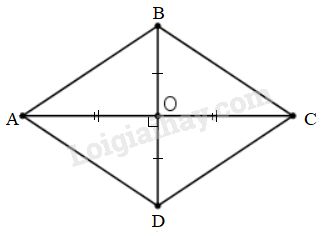
Xét hình thoi \(ABCD\) có \(BD=8\,cm,\)\(AC=10\,cm\).
gọi \(O\) là giao điểm của hai đường chéo.
Theo tính chất đường chéo hình thoi ta có:
\(AC\bot BD, OA=OC=\dfrac{{AC}}{2} = \dfrac{{10}}{2}\)\(\, = 5\,\,cm,\)
\(OB=OD=\dfrac{{BD}}{2} = \dfrac{8}{2} = 4\,\,cm\)
Áp dụng định lí Pytago vào tam giác \(ABO\) vuông tại \(O\) ta có:
\(A{B^2} = O{A^2} + O{B^2}= {5^2}+{4^2}=41\) nên \(AB = \sqrt {41} \,cm \).
Vậy câu trả lời (B) là đúng.
dapandethi.vn
