Đề bài
Tính các góc của tam giác \(ABC\), biết \(AB = 3cm,AC = 4cm\) và \(BC = 5cm.\)
Phương pháp giải - Xem chi tiết
Sử dụng tỉ số lượng giác của góc nhọn: \(\sin \alpha = \dfrac{{AB}}{{BC}}\) (hình vẽ)

Định lí Pytago đảo vào tam giác ABC:
Nếu \(A{B^2} + A{C^2} = B{C^2}\) thì tam giác \(ABC\) vuông tại \(A.\)
Lời giải chi tiết
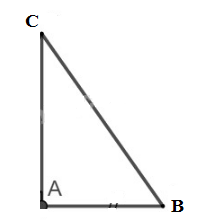
Ta có:
\(AB = 3 \Rightarrow A{B^2} = {3^2} = 9\)
\(AC = 4 \Rightarrow A{C^2} = {4^2} = 16\)
\(BC = 5 \Rightarrow B{C^2} = {5^2} = 25\)
Ta có:
\(A{B^2} + A{C^2}\) \(=9 + 16 = 25 = B{C^2}\)
Suy ra tam giác \(ABC\) vuông tại \(A\).
Ta có: \(\sin \widehat B = \dfrac{{AC}}{{BC}} = \dfrac{4 }{ 5} = 0,8\)\( \Rightarrow \widehat B = 53^\circ 8'\)
\(\widehat C = 90^\circ - \widehat B = 90^\circ - 53^\circ 8' = 36^\circ 52'\)
dapandethi.vn
