Đề bài
Đoạn thẳng \(LN\) vuông góc với đoạn thẳng \(AB\) tại trung điểm \(N\) của \(AB\); \(M\) là một điểm của đoạn thẳng \(LN\) và khác với \(L,N\). Hãy so sánh các góc \(\widehat {LAN}\) và \(\widehat {MBN}\).
Phương pháp giải - Xem chi tiết
Cho hình vẽ:

Ta có: \(\tan \alpha = \dfrac{{AB}}{{AC}}.\)
Lời giải chi tiết
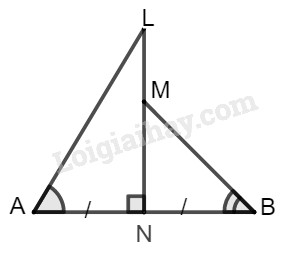
Tam giác \(ALN\) vuông tại \(N\) nên ta có:
\(tg\widehat {LAN} = \dfrac{{NL}}{{AN}}\) (1)
Tam giác \(BNM\) vuông tại \(N\) nên ta có:
\(tg\widehat {MBN} = \dfrac{{NM}}{{NB}}\) (2)
Mặt khác: \(AN = NB\) (gt) (3)
\(NL > NM\) (4) (do M thuộc đoạn thẳng LN)
Từ (1), (2), (3) và (4) suy ra: \(tg\widehat {MBN} < tg\widehat {LAN}\)
Suy ra: \(\widehat {MBN} < \widehat {LAN}\) ( vì \(\alpha \) tăng thì \(tg\alpha \) tăng).
dapandethi.vn
