Đề bài
Chứng minh rằng:
\(\dfrac{{{a^2}}}{{a + b}} + \dfrac{{{b^2}}}{{b + c}} + \dfrac{{{c^2}}}{{c + a}} = \dfrac{{{b^2}}}{{a + b}} \)\(\,+ \dfrac{{{c^2}}}{{b + c}} + \dfrac{{{a^2}}}{{c + a}}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Ta chứng minh hiệu hai vế bằng \(0\).
Sử dụng hằng đẳng thức số 3: \({A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\)
Lời giải chi tiết
Xét hiệu hai vế:
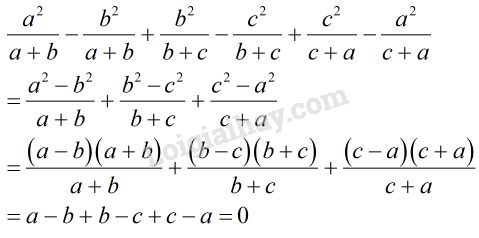
\(\Rightarrow\) \(\dfrac{{{a^2}}}{{a + b}} + \dfrac{{{b^2}}}{{b + c}} + \dfrac{{{c^2}}}{{c + a}} = \dfrac{{{b^2}}}{{a + b}} \)\(\,+ \dfrac{{{c^2}}}{{b + c}} + \dfrac{{{a^2}}}{{c + a}}\)
dapandethi.vn
