Video hướng dẫn giải
LG a.
Thực hiện phép chia:
\((2{x^4}-4{x^3} + 5{x^2} + 2x - 3):\)\(\,(2{x^2}-1)\).
Phương pháp giải:
- Áp dụng qui tắc chia đa thức cho đa thức.
Giải chi tiết:
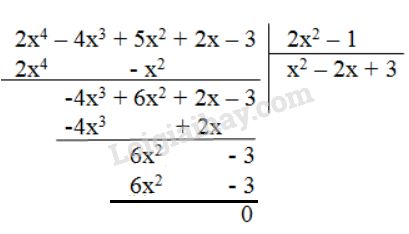
Vậy \(\left( {2{{\rm{x}}^4} - 4{{\rm{x}}^3} + 5{{\rm{x}}^2} + 2{\rm{x}} - 3} \right):\left( {2{{\rm{x}}^2} - 1} \right) \) \(= {x^2} - 2{\rm{x}} + 3\)
LG b.
Chứng tỏ rằng thương tìm được trong phép chia trên luôn luôn dương với mọi giá trị của \(x\).
Phương pháp giải:
Để chứng tỏ rằng thương tìm được trong phép chia trên luôn luôn dương với mọi giá trị của \(x\) ta đưa thương về dạng \({A^2} + k > 0\) với mọi \(x\) và \(k>0\)
Giải chi tiết:
Thương tìm được có thể viết:
\({x^2} - 2x + 3 = \left( {{x^2} - 2x + 1} \right) + 2\)
\(= {\left( {x - 1} \right)^2} + 2 > 0\) với mọi \(x\)
(Vì \({\left( {x - 1} \right)^2} \geqslant 0\) với mọi \(x\) nên \( {\left( {x - 1} \right)^2} + 2 \ge 2>0\) với mọi \(x\))
Vậy thương tìm được luôn luôn dương với mọi giá trị của \(x\).
dapandethi.vn
