Đề bài
Hình thang \(ABCD \,(AB//CD)\) có \(AC\) và \(BD\) cắt nhau tại \(O, AD\) và \(BC\) cắt nhau tại \(K\). Chứng minh rằng \(OK\) đi qua trung điểm của các cạnh \(AB\) và \(CD\).
Phương pháp giải - Xem chi tiết
- Qua \(O\) kẻ đường thẳng song song với \(AB, CD\) cắt \(AD, BC\) lần lượt tại \(E, F\).
- Chứng minh \(\dfrac{{AN}}{{EO}}=\dfrac{{BN}}{{FO}}\).
- Chứng minh \(\dfrac{{EO}}{{DM}}=\dfrac{{FO}}{{CM}}\).
Lời giải chi tiết
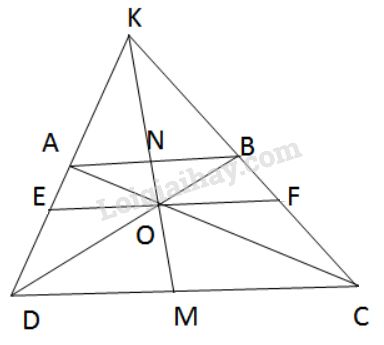
Qua \(O\) kẻ \(EF//AB\left( {E \in AD,F \in BC} \right)\) (h.54)
Trước hết hãy chứng minh rằng \(OE=OF\).
Xét \(\Delta DAC\) có \(EO//DC\) nên ta có:
\(\dfrac{{EO}}{{DC}} = \dfrac{{AO}}{{AC}}\) (1)
Xét \(\Delta DBC\) có \(OF//DC\) nên ta có:
\(\dfrac{{OF}}{{DC}} = \dfrac{{BO}}{{BD}}\) (2)
Vì \(AB//CD\) nên ta có:
\(\dfrac{{OA}}{{OC}} = \dfrac{{OB}}{{OD}}\) \( \Rightarrow \dfrac{{OA}}{{AC}} = \dfrac{{OB}}{{BD}}\) (3)
Từ các đẳng thức (1), (2) và (3) suy ra \(\dfrac{{EO}}{{DC}} = \dfrac{{OF}}{{DC}} \Rightarrow EO = OF\) (4)
Từ \(AB//EF\), ta có:
\(\dfrac{{AN}}{{EO}} = \dfrac{{KN}}{{KO}}\) và \(\dfrac{{KN}}{{KO}} = \dfrac{{BN}}{{OF}}\) suy ra \(\dfrac{{AN}}{{EO}} = \dfrac{{BN}}{{OF}}\) \( \Rightarrow AN = BN\) (vì \(EO = OF\)).
Vậy \(N\) là trung điểm của \(AB\).
Tương tự như vậy, từ \(CD//EF\), ta có:
\(\dfrac{{EO}}{{DM}} = \dfrac{{KO}}{{KM}}\) và \(\dfrac{{KO}}{{KM}} = \dfrac{{OF}}{{CM}}\); suy ra \(\dfrac{{EO}}{{DM}} = \dfrac{{OF}}{{CM}}\) \( \Rightarrow DM = CM\) (vì \(EO = OF\)).
Vậy \(M\) là trung điểm của \(CD\).
dapandethi.vn
