Đề bài
Cho tam giác \(ABC\) vuông ở \(A, AH\) và \(AM\) tương ứng là đường cao và đường trung tuyến kẻ từ \(A\) của tam giác đó. Qua điểm \(A\) kẻ đường thẳng \(mn\) vuông góc với \(AM.\) Chứng minh: \(AB\) và \(AC\) tương ứng là tia phân giác của các góc tạo bởi \(AH\) và hai tia \(Am, An\) của đường thẳng \(mn.\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Trong tam giác cân, hai góc ở đáy bằng nhau.
+) Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải chi tiết
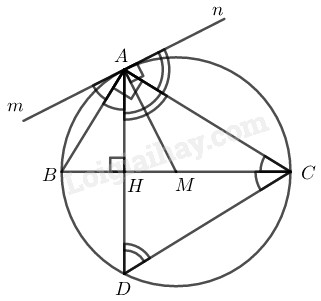
Vì \(∆ABC\) vuông tại \(A,\) có \(AM\) là đường trung tuyến ứng với cạnh huyền \(BC\)
\( \Rightarrow AM = MB = MC = \displaystyle{1 \over 2}BC\) (tính chất tam giác vuông)
Nên đường tròn tâm \(M\) bán kính \(MA\) đi qua \(A,B,C\)
Gọi \(D\) là giao điểm của \(AH\) với đường tròn \((M,MA).\)
Khi đó: \(BC \bot AD\) tại H nên H là trung điểm của AD (quan hệ giữa đường kính và dây của đường tròn)
\( \Rightarrow BC\) là trung trực của \(AD\)
\( \Rightarrow AC=CD\) (tính chất đường trung trực của đoạn thẳng)
\( \Rightarrow ∆ACD\) cân tại \(C\)
\( \Rightarrow \widehat{ADC}=\widehat{DAC}\) \((1)\)
Ta lại có: \(\widehat{ADC}=\widehat{nAC}\) (hệ quả của góc giữa tia tiếp tuyến và dây cung) \((2)\)
Từ \((1),(2)\) suy ra \(\widehat{DAC}=\widehat{nAC}\) hay \(\widehat{HAC}=\widehat{nAC}\)
Vậy \(AC\) là tia phân giác của \(\widehat {HAn}\)
Ta có: \(\widehat{ACB}=\widehat{mAB}\) (hệ quả của góc giữa tia tiếp tuyến và dây cung) \((3)\)
\( \widehat {BAH} + \widehat {ACB} = {90^o}\) (cùng phụ với góc \(\widehat {HAC}\)) \( (4)\)
Từ \((3),(4)\) suy ra \(\widehat {mAB} = \widehat {BAH}\).
Vậy \(AB\) là tia phân giác của \(\widehat {mAH}\).
dapandethi.vn
