Đề bài
Cho tam giác ABC cân tại A. Trên tia đối của tia BA lây điểm M, trên tia đối của tia CA lấy điểm N sao cho MB = NC. Kẻ \(MI \bot BC(I \in BC)\) và \(NK \bot BC(K \in BC).\) Chứng minh rằng :
a) \(\Delta MBI = \Delta NCK.\)
b) \(\Delta AIK\) cân.
c) IK // MN.
Lời giải chi tiết
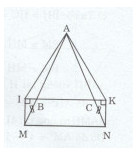
a)Ta có: \(\eqalign{ & \widehat {ABC} = \widehat {IBM} \cr & \widehat {ACB} = \widehat {KCN} \cr} \) (hai góc đối đỉnh)
Mà \(\widehat {ABC} = \widehat {ACB}(\Delta ABC\) cân tại A) nên \(\widehat {IBM} = \widehat {KCN.}\)
Xét tam giác MBI vuông tại I và tam giác NCK vuông tại K ta có:
\(\eqalign{ & \widehat {IBM} = \widehat {KCN}(cmt) \cr & MB = NC(gt) \cr} \)
Do đó: \(\Delta MBI = \Delta NCK\) (cạnh huyền - góc nhọn)
b) Ta có: AB = AC (tam giác ABC cân tại A) và BM = CN (giả thiết)
=>AB + BM = AC + CN => AM = AN.
Xét tam giác AIM và AKN ta có:
\(\eqalign{ & IM = KN(\Delta MBI = \Delta NCK) \cr & \widehat {IMA} = \widehat {KNA}(\Delta MBI = \Delta NCK) \cr} \)
Do đó: \(\Delta AIM = \Delta AKN(c.g.c) \Rightarrow AI = AK.\) Vậy tam giác AIK cân tại A.
c) Tam giác ABC cân tại A \(\Rightarrow \widehat {ABC} = \widehat {ACB}.\) Do đó: \(\widehat {ABC} = {{{{180}^0} - \widehat {BAC}} \over 2}(1)\)
Mặt khác AM = AN => tam giác AMN cân tại A \(\Rightarrow \widehat {AMN} = \widehat {ANM}.\)
Do đó: \(\widehat {AMN} = {{{{180}^0} - \widehat {BAC}} \over 2}(2)\)
Từ (1) và (2) ta có: \(\widehat {ABC} = \widehat {AMN}.\)
Mà hai góc ABC và AMN đồng vị. Vậy IK // MN.
dapandethi.vn
