Đề bài
Cho tứ diện \(ABCD\). Gọi \(G\) là trọng tâm của tam giác \(ABC\). Chứng minh rằng:
\(\overrightarrow {G{\rm{D}}} .\overrightarrow {GA} + \overrightarrow {G{\rm{D}}} .\overrightarrow {GB} + \overrightarrow {G{\rm{D}}} .\overrightarrow {GC} = 0\)
Phương pháp giải - Xem chi tiết
Sử dụng lý thuyết: \(G\) là trọng tâm của tam giác \(ABC\) nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \).
Lời giải chi tiết
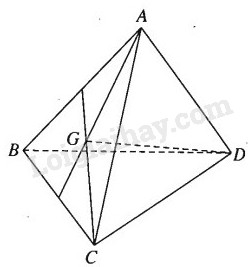
Ta có:
\(\eqalign{
& \overrightarrow {G{\rm{D}}} .\overrightarrow {GA} + \overrightarrow {GD} .\overrightarrow {GB} + \overrightarrow {GD} .\overrightarrow {GC} \cr
& = \overrightarrow {GD} .\left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) \cr
& = \overrightarrow {GD} .\overrightarrow 0 = 0 \cr} \)
(Vì \(G\) là trọng tâm của tam giác \(ABC\) nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \) )
dapandethi.vn
