Đề bài
Một người lái ô tô dự định đi từ A đến B với vận tốc \(48 km/h\). Nhưng sau khi đi được một giờ với vận tốc ấy, ô tô bị tàu hỏa chắn đường trong \(10\) phút. Do đó, để kịp đến B đúng thời gian đã định, người đó phải tăng vận tốc thêm \(6 km/h\). Tính quãng đường AB.
Phương pháp giải - Xem chi tiết
B1: Đặt quãng đường AB là ẩn.
B2: Biểu diễn các đại lượng còn lại theo ẩn.
B3: Lập phương trình biểu diễn mối quan hệ giữa các đại lượng và giải phương trình đó.
B4: Kết luận.
Lời giải chi tiết
Gọi \(x\) là độ dài quãng đường AB (điều kiện \(x > 0\,( km)\))

Lập bảng:
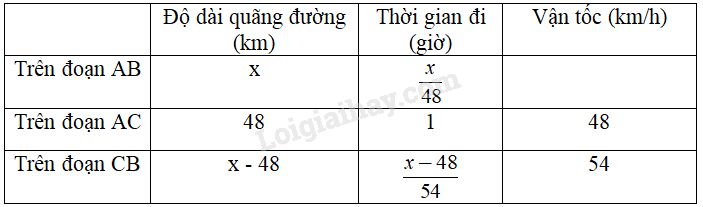
Thời gian dự định đi quãng đường AB bằng thời gian đi với vận tốc \(48km/h\) trên cả đoạn đường AB và bằng tổng thời gian đi trên hai đoạn AC và CB cộng thêm \( \dfrac{1}{6}\) giờ (\(10\) phút chờ tàu). Do đó ta có phương trình:
\(1 + \dfrac{1}{6} + \dfrac{{x - 48}}{{54}} = \dfrac{x}{{48}}\)
Giải phương trình:
\(1 + \dfrac{1}{6} + \dfrac{{x - 48}}{{54}} = \dfrac{x}{{48}}\)
\(\begin{array}{l}
\Leftrightarrow \dfrac{{432 + 72 + 8\left( {x - 48} \right)}}{{432}} = \dfrac{{9x}}{{432}}\\
\Leftrightarrow 432 + 72 + 8x - 384 = 9x
\end{array}\)
\( \Leftrightarrow x = 120\) (thỏa mãn).
Trả lời: Vậy quãng đường AB dài \(120\) km.
dapandethi.vn
