Đề bài
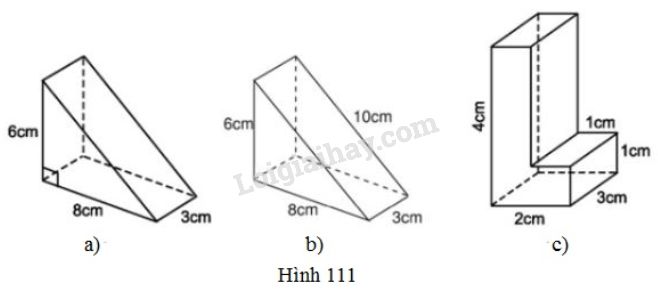
Các hình a, b, c (h.111) gồm một hoặc nhiều lăng trụ đứng. Hãy tính thể tích và diện tích toàn phần của chúng theo các kích thước đã cho trên hình.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng các công thức:
- Diện tích xung quanh: \( S_{xq} =C.h \), trong đó \(C\) là chu vi đáy, \(h\) là chiều cao.
- Diện tích toàn phần = diện tích xung quanh + diện tích hai đáy.
Lời giải chi tiết
+) Hình a là lăng trụ đứng có chiều cao là \(3cm\) và đáy là tam giác vuông có hai cạnh góc vuông là \(6cm,\; 8cm\).
Suy ra cạnh huyền là \(\sqrt{6^{2}+8^{2}} = \sqrt{36+64} = \sqrt{100} = 10\) \((cm)\).
Diện tích đáy là : \(S = \dfrac{1}{2}6 . 8 = 24(cm^2) \)
Thể tích lăng trụ là: \(V = S.h = 24.3 = 72(cm^3) \)
Diện tích xung quanh lăng trụ là:
\(S_{xq} =2p.h = (6+8+10).3 = 24.3 \)\(=72 \) \((cm^2)\)
Diện tích toàn phần lăng trụ là:
\(S_{tp} =S_{xq}+2. S_{đ} = 72 +2.24 =120\) \((cm^2)\)
+) Hình b là lăng trụ đứng tam giác có ba kích thước là \(6cm,\, 8cm, \,10cm\); chiều cao lăng trụ là \(3cm\).
Vì \(6^2 + 8^2 = 36 + 64 = 100 = 10^2 \) nên đáy lăng trụ là tam giác vuông có hai cạnh góc vuông là \(6cm,\, 8cm\). Do đó, bài toán này quay về bài toán ở hình a, ta thu được kết quả:
\(V= 72cm^3; \quad S_{xq} = 72 cm^2;\)\( \quad S_{tp} =120(cm^2)\).
+) Hình c là hình gồm hai lăng trụ đứng: Hình lăng trụ một là hình hộp chữ nhật có các kích thước \(4cm, \; 1cm,\; 3cm\) ; hình lăng trụ hai là hình hộp chữ nhật có các kích thước \(1cm,\;1cm, \; 3cm\).
Thể tích lăng trụ một là: \( V_1 = 4.1.3 =12 (cm^3)\)
Thể tích lăng trụ hai là: \( V_2 = 1.1.3 =3 (cm^3)\)
Thể tích lăng trụ đã cho là
\( V = V_1+ V_2 = 12 +3 =15 (cm^3)\)
Diện tích xung quanh của lăng trụ một là:
\( S_{xq1} = 2.(3+1).4 =32 (cm^2)\)
Diện tích một đáy của lăng trụ một là:
\( S_{đ1} = 3.1 =3 (cm^2) \)
Diện tích toàn phần của lăng trụ một là:
\( S_{tp1} =S_{xq1} +2. S_{đ1} = 32 +2.3 =38 \) \((cm^2)\)
Diện tích xung quanh của lăng trụ hai là:
\( S_{xq2} = 2.(1+3).1 =8 (cm^2)\)
Diện tích một đáy của lăng trụ hai là:
\( S_{đ2} = 3.1 =3 (cm^2) \)
Diện tích toàn phần của lăng trụ hai là:
\( S_{tp2} =S_{xq2} +2. S_{đ2} = 8 +2.3=14\) \( (cm^2)\)
Diện tích toàn phần của lăng trụ đã cho bằng tổng diện tích toàn phần của lăng trụ 1 và 2 trừ đi 2 phần diện tích chung là hình chữ nhật với các kích thước \(1cm,\; 3cm\). Do đó:
\( S_{tp} =S_{tp1} +S_{tp2} - 2. S_{hcn} \)
\(=38 + 14 - 2.3.1 =46 (cm^2)\)
dapandethi.vn
