Đề bài
Đố: Đức tính đáng quý.
Hãy viết mỗi biểu thức sau dưới dạng bình phương hoặc lập phương của một tổng hoặc một hiệu, rồi điền chữ cùng dòng với biểu thức đó vào bảng cho thích hợp. Sau khi thêm dấu, em sẽ tìm ra một trong những đức tính quý báu của con người.
\({x^3} - 3{x^2} + 3x - 1\) \(N\)
\(16 + 8x + {x^2}\) \( U\)
\(3{x^2} + 3x + 1 + {x^3}\) \(H\)
\(1 - 2y + {y^2}\) \(Â\)

Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng: Hằng đẳng thức lập phương của một tổng, lập phương của một hiệu, bình phương của một tổng hoặc một hiệu.
\((A+B)^2=A^2+2AB+B^2\)
\((A-B)^2=A^2-2AB+B^2\)
\({\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\)
\({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\)
Lời giải chi tiết
Ta có:
N: \({x^3} - 3{x^2} + 3x - 1 \)
\(= {x^{3}} - 3.{x^2}.1 + 3.x{.1^2} - {1^3} = {\left( {x - 1} \right)^3}\)
U: \(16 + 8x + {x^2} = {4^2} + 2.4.x + {x^2} \)
\(= {\left( {4 + x} \right)^2} = {\left( {x + 4} \right)^2}\)
H: \(3{x^2} + 3x + 1 + {x^3} \)
\(= {x^3} + 3{x^2} + 3x + 1 \)
\(= {x^3} + 3.{x^2}.1 + 3.x{.1^2} + {1^3} \)
\(= {\left( {x + 1} \right)^3} = {\left( {1 + x} \right)^3}\)
Â: \(1 - 2y + {y^2} = {y^2} - 2y + 1 \)
\(= {y^2} - 2.y.1 + {1^2} \)
\(= {\left( {y - 1} \right)^2} = {\left( {1 - y} \right)^2}\)
Ta điền vào bảng như sau:
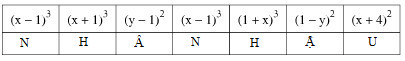
Vậy: Đức tính đáng quý là "NHÂN HẬU"
Chú ý:
Có thể khai triển các biểu thức \({\left( {x - 1} \right)^3},{\left( {x + 1} \right)^3},{\left( {y - 1} \right)^2},{\left( {x + 4} \right)^2}\) ... để tìm xem kết quả ứng với chữ nào và điền vào bảng.
dapandethi.vn
