Đề bài
Tam giác \(ABC\) nội tiếp đường tròn \((O)\) có \(\widehat A > \widehat B > \widehat C.\) Gọi \(OH, OI, OK\) theo thứ tự là khoảng cách từ \(O\) đến \(BC,\)\( AC,\)\( AB.\) So sánh các độ dài \(OH, OI, OK.\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức:
+) Trong một tam giác, cạnh nào đối diện với góc lớn hơn thì cạnh đó lớn hơn.
+) Trong hai dây của một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.
Lời giải chi tiết
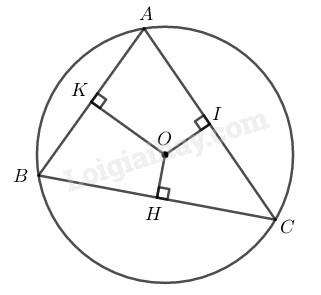
Tam giác \(ABC\) có \(\widehat A > \widehat B > \widehat C\) nên suy ra:
\(BC > AC > AB\) (cạnh đối diện góc lớn hơn thì lớn hơn)
Ta có \(AB,\) \(BC,\) \(AC\) lần lượt là các dây cung của đường tròn \((O)\)
Mà \(BC > AC > AB\) nên suy ra:
\(OH < OI < OK\) ( dây lớn hơn thì gần tâm hơn).
dapandethi.vn
