Bài 26 trang 67 SBT toán 9 tập 1

Đề bài

Cho hai đường thẳng

 \(y = ax + b\)                   (d)

\(y = a’x + b’\)                 (d’)

Chứng minh rằng :

Trên cùng một mặt phẳng tọa độ , hai đường thẳng (d) và (d’) vuông góc với nhau khi và chỉ khi a. a’ = 1.

Lời giải chi tiết

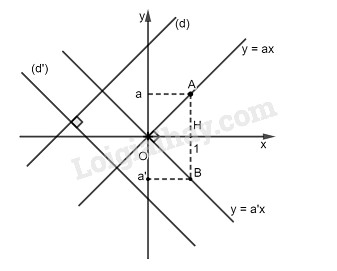
Qua gốc tọa độ, kẻ đường thẳng \(y = ax\) // (d) và \(y = ax\) // (d’).

*Chứng minh (d) vuông góc với (d’) thì \(a. a’ = -1\)

Không mất tính tổng quát, giả sử \(a > 0\)

Khi đó góc tạo bởi tia \(Ox\) và đường thẳng \(y = ax\) là góc nhọn.

Suy ra góc tạo bởi tia \(Ox\) và đường thẳng \(y = a’x\) là góc tù ( vì các góc tạo bởi đường thẳng \(y = ax\) và đường thẳng \(y = a’x\) với tia \(Ox\) hơn kém nhau \(90^0).\)

Suy ra: \(a’ < 0\)

Mà đường thẳng \(y = ax\) đi qua \(A(1;a)\), đường thẳng \(y = a’x\) đi qua \(B(1;a’)\)

nên đoạn \(AB\) vuông góc với \(Ox\) tại điểm H có hoành độ bằng \(1.\)

Vì \(\left( {\rm{d}} \right) \bot \left( {{\rm{d'}}} \right)\) nên hai đường thẳng \(y = ax\) và \(y = a’x\) vuông góc với nhau

Suy ra: \(\widehat {AOB} = {90^0}\)

Tam giác vuông AOB có \(OH \bot AB\). Theo hệ thức lượng trong tam giác vuông ta có : \(O{H^2} = HA.HB\)

Hay: \(a.\left| {a'} \right| = 1 \Leftrightarrow a.\left( { - a'} \right) = 1 \Leftrightarrow a.a' =  - 1\)

Vậy nếu (d) vuông góc với (d’) thì \( a.a’ = -1\)

*Chứng minh \(a.a' =  - 1\) thì (d) vuông góc với (d’)

Ta có : \(a.a' =  - 1\)\( \Leftrightarrow a.\left| {a'} \right| = 1\) hay \(HA.HB = O{H^2}\)

Suy ra: \(\dfrac{{HA}}{{OH}} = \dfrac{{OH}}{{HB}}\) mà \( \widehat {OHA} = \widehat {OHB} = {90^0}\)

Suy ra: \(\Delta OHA\) đồng dạng \(\Delta BHO \)\(\Rightarrow \widehat {AOH} = \widehat {OBH}\)

Mà \(\widehat {OBH} + \widehat {BOH} = {90^0} \)\(\Rightarrow \widehat {AOH} + \widehat {BOH} = {90^0}\)\(\Rightarrow \widehat {AOH}=90^0\)

Suy ra \(OA \bot OB\) hay hai đường thẳng \(y = ax\) và \(y = a’x\) vuông góc với nhau.

Vậy \(\left( {\rm{d}} \right) \bot \left( {{\rm{d'}}} \right)\).

dapandethi.vn