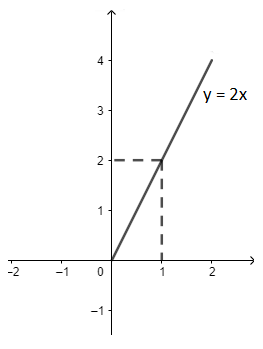Lập bảng biến thiên và vẽ đồ thị của môi hàm số
LG a
\(y = |2x - 3|\);
Phương pháp giải:
Sử dụng kiến thức về giá trị tuyệt đối và cách vẽ bảng biến thiên.
Lời giải chi tiết:
Ta có thể viết
\(y = \left\{ \begin{array}{l}2x - 3,x \ge \dfrac{3}{2}\\ - 2x + 3,x < \dfrac{3}{2}\end{array} \right.\)
Từ đó có bảng biến thiên và đồ thị của hàm số \(y = |2x - 3|\)(h.32)

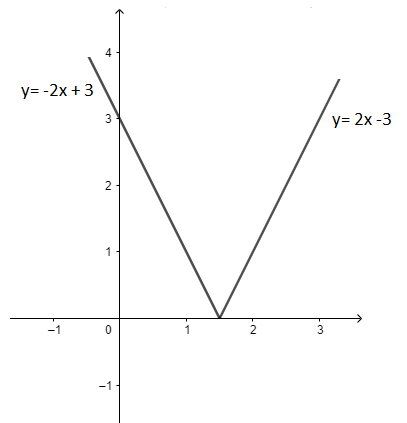
LG b
\(y = | - \dfrac{3}{4}x + 1|\)
Phương pháp giải:
Sử dụng kiến thức về giá trị tuyệt đối và cách vẽ bảng biến thiên.
Lời giải chi tiết:
Ta có thể viết
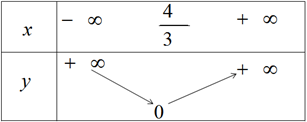
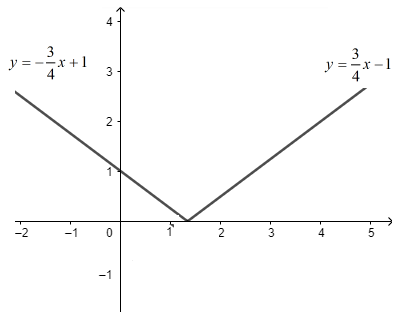
\(y = \left\{ \begin{array}{l} - \dfrac{3}{4}x + 1,x \le \dfrac{4}{3}\\\dfrac{3}{4}x - 1,x > \dfrac{4}{3}\end{array} \right.\)
Bảng biến thiên và đồ thị của hàm số \(y = | - \dfrac{3}{4}x + 1|\)(h.33)
LG c
\(y = x + |x|\).
Phương pháp giải:
Sử dụng kiến thức về giá trị tuyệt đối và cách vẽ bảng biến thiên.
Lời giải chi tiết:
Với \(x \ge 0\) thì \(y = x + \left| x \right| = x + x = 2x\)
Với \(x < 0\) thì \(y = x + \left| x \right| = x - x = 0\)
Ta có:
\(\begin{array}{l}
y = x + |x|\; = x + \sqrt {{x^2}} \quad \\
\Rightarrow y' = 1 + \frac{{2x}}{{2\sqrt {{x^2}} }} = 1 + \frac{x}{{|x|}} = \left\{ \begin{array}{l}
2\quad x \ge 0\\
0\quad x < 0
\end{array} \right.
\end{array}\)
\( \Rightarrow y' \ge 0\;\;\forall x\)
Bảng biến thiên:
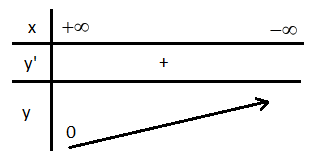
Đồ thị của hàm số \(y = x + |x|\)được vẽ trên hình.