Viết phương trình đường thẳng \(y = ax + b\) ứng với hình sau
LG a
Phương pháp giải:
Gọi phương trình tổng quát của đường thẳng sau đó xác định các hệ số \(a\) và \(b\) ta dựa vào tọa độ các điểm mà đồ thị đi qua, lập hệ phương trình có hai ẩn \(a\) và \(b\).
Lời giải chi tiết:
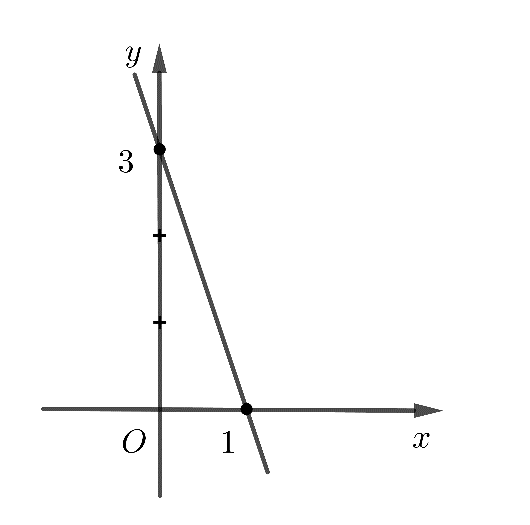
Ta thấy đường thẳng \(y = ax + b\) đi qua hai điểm \((0;3)\) và \((1;0)\). Vậy ta có:
\(\left\{ \begin{array}{l}3 = b\\0 = a + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 3\\b = 3\end{array} \right.\)
Đường thẳng có phương trình là \(y = - 3x + 3\).
LG b
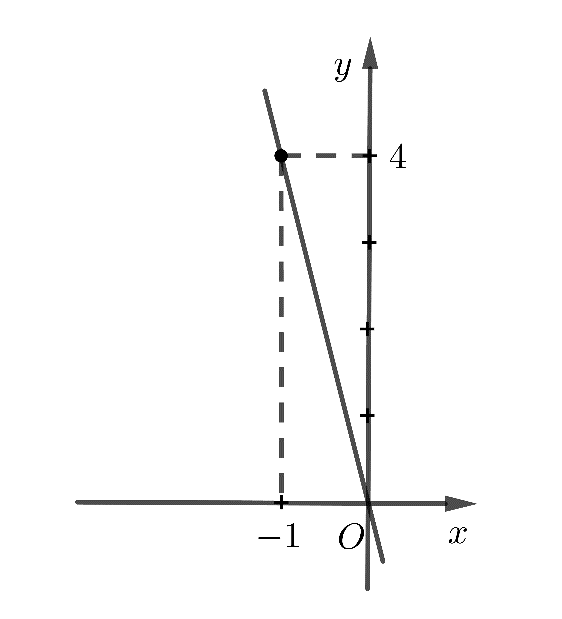
Phương pháp giải:
Gọi phương trình tổng quát của đường thẳng sau đó xác định các hệ số \(a\) và \(b\) ta dựa vào tọa độ các điểm mà đồ thị đi qua, lập hệ phương trình có hai ẩn \(a\) và \(b\).
Lời giải chi tiết:
Ta thấy đường thẳng \(y = ax + b\) đi qua hai điểm \(\left( {0;0} \right)\) và \(\left( { - 1;4} \right)\).
Vậy ta có:\(\left\{ \begin{array}{l}0 = b\\4 = a.\left( { - 1} \right) + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 4\\b = 0\end{array} \right.\)
Đường thẳng có phương trình là \(y = - 4x\).
dapandethi.vn
