Đề bài
Biết \(\sin \alpha = \dfrac{2}{3}\). Tính giá trị của biểu thức \(B = \dfrac{{\cot \alpha - \tan \alpha }}{{\cot \alpha + \tan \alpha }}\)
Phương pháp giải - Xem chi tiết
Sử dụng hệ thức \( \sin ^2x+\cos ^2x=1\).
Lời giải chi tiết
Ta có: \(B = \dfrac{{\cot \alpha - \tan \alpha }}{{\cot \alpha + \tan \alpha }}\) \( = \dfrac{{\dfrac{{\cos \alpha }}{{\sin \alpha }} - \dfrac{{\sin \alpha }}{{\cos \alpha }}}}{{\dfrac{{\cos \alpha }}{{\sin \alpha }} + \dfrac{{\sin \alpha }}{{\cos \alpha }}}}\) \( = \dfrac{{\dfrac{{{{\cos }^2}\alpha - {{\sin }^2}\alpha }}{{\sin \alpha \cos \alpha }}}}{{\dfrac{{{{\cos }^2}\alpha + {{\sin }^2}\alpha }}{{\sin \alpha \cos \alpha }}}}\) \( = \dfrac{{{{\cos }^2}\alpha - {{\sin }^2}\alpha }}{{{{\cos }^2}\alpha + {{\sin }^2}\alpha }}\)
\( = {\cos ^2}\alpha - {\sin ^2}\alpha \).
Mà \(\sin \alpha = \dfrac{2}{3}\) \( \Rightarrow {\cos ^2}\alpha = 1 - {\sin ^2}\alpha \) \( = 1 - \dfrac{4}{9} = \dfrac{5}{9}\)
Thay vào \(B\) ta được \(B = \dfrac{5}{9} - \dfrac{4}{9} = \dfrac{1}{9}\)
Vậy \(B = \dfrac{1}{9}\).
Cách khác:
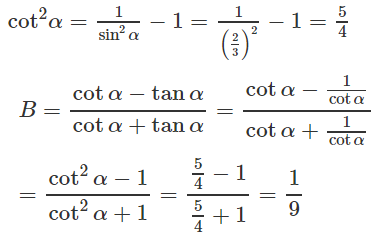
dapandethi.vn
