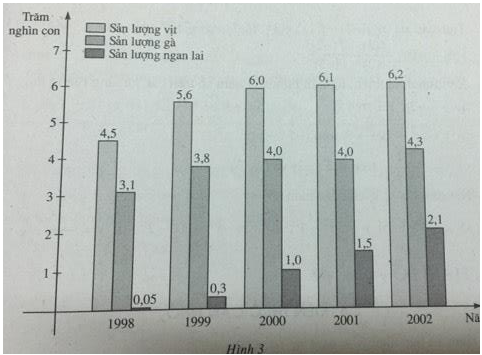
Biểu đồ sau (h.3) biểu thị sản lượng vịt, gà và ngan lai qua 5 năm của một trang trại. Coi \(y = f(x),y = g(x)\) và \(y = h(x)\) tương ứng là các hàm số biểu thị sự phụ thuộc số vịt, số gà và số ngan lai vào thời gian \(x\). Qua biểu đồ, hãy:
LG a
Tìm tập xác định của mỗi hàm số đã nêu.
Phương pháp giải:
Sử dụng các kiến thức về hàm số, tập xác định của hàm số.
Lời giải chi tiết:
Tập xác định của cả ba hàm số \(y = f(x),y = g(x)\)và \(y = h(x)\) là :
\(D = {\rm{\{ }}1998;1999;2000;2001;2002\} \)
LG b
Tìm các giá trị \(f(2002), g(1999),\) \( h(2000)\) và nêu ý nghĩa của chúng;
Phương pháp giải:
Sử dụng các kiến thức về hàm số, tập xác định của hàm số.
Lời giải chi tiết:
\(f(2002) = 620{\rm{ }}000\) (con) ; \(g(1999) = 380{\rm{ }}000\) (con) ; \(h(2000) = 100{\rm{ }}000\) (con)
Năm \(2002\) sản lượng của trang trại là \(620 000\) con vịt ; năm \(1999\) sản lượng là \(380 000\) con gà ; năm \(2000\) trang trại có sản lượng là \(100 000\) con ngan lai.
LG c
Tìm hiệu \(h(2002) – h(1999)\) và nêu ý nghĩa của nó.
Phương pháp giải:
Sử dụng các kiến thức về hàm số, tập xác định của hàm số.
Lời giải chi tiết:
\(h(2002) - h(1999) = 210{\rm{ }}000 - 30{\rm{ }}000 \)\(= 180{\rm{ }}000\) (con).
Sản lượng ngan lai của trang trại năm \(2002\) tăng \(180 000\) con so với năm \(1999\).
dapandethi.vn
