Đề bài
Cho hình bình hành \(ABCD\). Dựng \(\overrightarrow {AM} = \overrightarrow {BA} \), \(\overrightarrow {MN} = \overrightarrow {DA} \), \(\overrightarrow {NP} = \overrightarrow {DC} \), \(\overrightarrow {PQ} = \overrightarrow {BC} \). Chứng minh \(\overrightarrow {AQ} = \overrightarrow 0 \)
Phương pháp giải - Xem chi tiết
Dựng hình và nhận xét.
Lời giải chi tiết
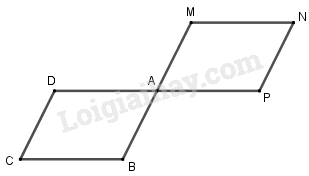
+ Trên tia \(BA\) lấy điểm \(M\) sao cho \(BA = AM\), khi đó \(\overrightarrow {AM} = \overrightarrow {BA} \).
+ Qua \(M\) kẻ đường thẳng song song \(DA\), lấy điểm \(N\) sao cho \(MN = DA\) và \(\overrightarrow {MN} \) cùng hướng \(\overrightarrow {DA} \). Khi đó ta được \(\overrightarrow {MN} = \overrightarrow {DA} \).
+ Qua \(N\) kẻ đường thẳng song song \(DC\), lấy điểm \(P\) sao cho \(NP = DC\) và \(\overrightarrow {NP} \) cùng hướng \(\overrightarrow {DC} \). Khi đó ta được \(\overrightarrow {NP} = \overrightarrow {DC} \).
+ Qua \(P\) kẻ đường thẳng song song \(BC\), lấy điểm \(Q\) sao cho \(PQ = BC\) và \(\overrightarrow {PQ} \) cùng hướng \(\overrightarrow {BC} \). Khi đó ta được \(\overrightarrow {PQ} = \overrightarrow {BC} \).
Lại có \(\overrightarrow {MA} = \overrightarrow {AB} \) và \(\overrightarrow {NP} = \overrightarrow {DC} = \overrightarrow {AB} \).
Suy ra \(AM = NP\) và \(AM//NP\). Vậy tứ giác \(AMNP\) là hình bình hành.
Ta có \(\overrightarrow {PQ} = \overrightarrow {BC} \); \(\overrightarrow {MN} = \overrightarrow {DA} = \overrightarrow {CB} \)
Suy ra \(PQ = MN\) và \(PQ//MN\).
Vậy tứ giác \(MNPQ\) là hình bình hành (2).
Từ (1) và (2) suy ra \(A \equiv Q\) hay \(\overrightarrow {AQ} = \overrightarrow 0 \).
dapandethi.vn
