Đề bài
Cho tứ giác \(ABCD\). Gọi \(M,N,P\) và \(Q\) lần lượt là trung điểm của các cạnh \(AB,BC,CD\) và\(DA\). Chứng minh \(\overrightarrow {NP} = \overrightarrow {MQ} \)và \(\overrightarrow {PQ} = \overrightarrow {NM} \).
Phương pháp giải - Xem chi tiết
Chứng minh \(MNPQ\) là hình bình hành, từ đố suy ra điều phải chứng minh.
Lời giải chi tiết
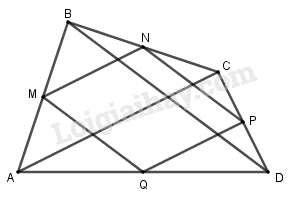
Ta thấy, \(MN\) là đường trung bình của tam giác \(ABC\) nên \(MN//AC\) và \(MN = \dfrac{1}{2}AC\).
\(PQ\) là đường trung bình của tam giác \(ADC\) nên \(PQ//AC\) và \(PQ = \dfrac{1}{2}AC\).
Do đó \(NM//PQ\) và \(MN = PQ\).
Vậy tứ giác \(MNPQ\) là hình bình hành nên \(\overrightarrow {NP} = \overrightarrow {MQ} ,\overrightarrow {PQ} = \overrightarrow {NM} \).
dapandethi.vn
