Bài 1.47 trang 42 SBT hình học 10

Đề bài

Cho lục giác đều \(ABCDEF\). Chọn hệ tọa độ \((O;\overrightarrow i ,\overrightarrow j )\), trong đó \(O\) là tâm của lục giác đều, hai véc tơ \(\overrightarrow i \) và \(\overrightarrow {OD} \) cùng hướng, \(\overrightarrow j \) và \(\overrightarrow {EC} \) cùng hướng . Tính tọa độ các đỉnh của lục giác biết độ dài của lục giác là \(6\).

Lời giải chi tiết

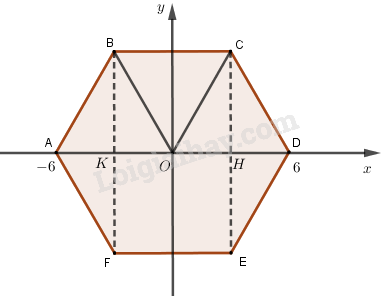
Từ hình vẽ ta thấy \(A\left( { - 6;0} \right)\) và \(D\left( {6;0} \right)\) (do các tam giác \(AOB\) và \(COD\) đều nên \(OA = OD = AB = 6\)).

Gọi \(H,K\) lần lượt là hình chiếu của \(C,B\) lên trục \(Ox\).

Khi đó \(CH = DC\sin {60^0} = \dfrac{{6\sqrt 3 }}{2} = 3\sqrt 3 \)

\(OH = \sqrt {O{C^2} - C{H^2}}  \) \(= \sqrt {{6^2} - {{\left( {3\sqrt 3 } \right)}^2}}  = 3\)

Do đó \(C\left( {3;3\sqrt 3 } \right)\).

B đối xứng với C qua Oy nên B(-3; 3√3)

E đối xứng với C qua Ox nên E(3; -3√3)

F đối xứng với C qua O nên F(-3; -3√3))

Vậy \(A\left( { - 6;0} \right)\), \(D\left( {6;0} \right)\), \(B\left( { - 3;3\sqrt 3 } \right)\), \(C\left( {3;3\sqrt 3 } \right)\), \(E\left( {3; - 3\sqrt 3 } \right)\), \(F\left( { - 3; - 3\sqrt 3 } \right)\) .

dapandethi.vn