Đề bài
Cho tam giác \(ABC\). Các điểm \(M(1;1),N(2;3),P(0; - 4)\) lần lượt là trung điểm các cạnh \(BC, CA, AB\). Tính tọa độ các đỉnh của tam giác.
Phương pháp giải - Xem chi tiết
Dựng hình và nhận xét các véc tơ bằng nhau.
Lời giải chi tiết
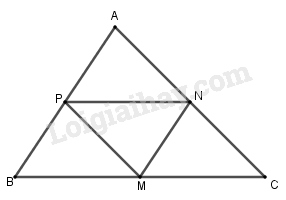
Ta có: \(\overrightarrow {MN} = (1;2)\); \(\overrightarrow {PA} = \left( {{x_A};{y_A} + 4} \right)\)
Vì \(\overrightarrow {PA} = \overrightarrow {MN} \) suy ra \(\left\{ \begin{array}{l}{x_A} = 1\\{y_A} + 4 = 2\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}{x_A} = 1\\{y_A} = - 2\end{array} \right.\)
Tương tự, ta tính được \(\left\{ \begin{array}{l}{x_B} = - 1\\{y_B} = - 6\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}{x_C} = 3\\{y_C} = 8\end{array} \right.\)
Vậy tọa độ các đỉnh của tam giác là\(A(1; - 2),B( - 1; - 6),C(3;8)\)
dapandethi.vn
