Cho A và B là hai tập hợp hữu hạn. Kí hiệu |A| là số phần tử của tập hợp A.
LG a
Chứng minh rằng nếu \(A \cap B = \emptyset \) thì \(\left| {A \cup B} \right| = \left| A \right| + \left| B \right|\)
Lời giải chi tiết:
Hiển nhiên.
LG b
Chứng minh rằng \(B \cup \left( {A\backslash B} \right) = A \cup B\) và \(B \cap \left( {A\backslash B} \right) = \emptyset \)
Lời giải chi tiết:
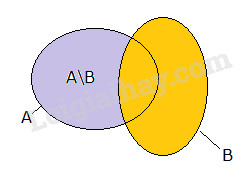
Từ biểu đồ Ven ta suy ra đpcm.
LG c
Chứng minh rằng \(A = \left( {A \cap B} \right) \cup \left( {A\backslash B} \right)\)
Lời giải chi tiết:
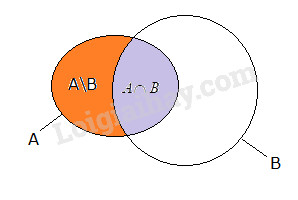
Từ biểu đồ Ven ta suy ra đpcm.
LG d
Từ đó suy ra công thức sau
\(\left| {A \cup B} \right| = \left| A \right| + \left| B \right| - \left| {A \cap B} \right|\)
Lời giải chi tiết:
Ta có \(\left| {A \cup B} \right| = \left| B \right| + \left| {A\backslash B} \right|,\) (do câu a và b) (1)
Lại có \(A = \left( {A\backslash B} \right) \cup \left( {A \cap B} \right)\) (do c))
Do đó, \(\left| A \right| = \left| {A\backslash B} \right| + \left| {A \cap B} \right|\)
Vậy
\(\left| {A\backslash B} \right| = \left| A \right| - \left| {A \cap B} \right|\) (2)
Thay (2) vào (1) ta được
\(\left| {A \cup B} \right| = \left| A \right| + \left| B \right| - \left| {A \cap B} \right|\)
dapandethi.vn
