Đề bài
Cho một nửa đường tròn bán kính \(AB\). Điểm \(M\) chạy trên nửa đường tròn. Kẻ \(MH\) vuông góc với \(AB\) tại \(H.\) Đặt \(MH = x.\)
\(a)\) Chứng minh rằng hai tam giác \(AHM\) và \(MHB\) đồng dạng.
\(b)\) Chứng minh rằng \(AH.BH = M{H^2}\).
\(c)\) Khi \(M\) chuyển động thì \(x\) thay đổi, do đó tích \(AH.BH\) cũng thay đổi theo. Kí hiệu tích \(AH.BH\) bởi \(P(x).\) Hỏi \(P(x)\) có phải là một hàm số của biến số \(x\) hay không\(?\) Viết công thức biểu thị hàm số này.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Góc nội tiếp chắn nửa đường tròn là góc vuông.
+) Nếu hai tam giác đồng dạng ta suy ra được các cạnh tương ứng tỉ lệ.
+) Nếu đại lượng \(y\) phụ thuộc vào đại lượng thay đổi \(x\) sao cho với mỗi giá trị của \(x\), ta luôn xác định được chỉ một giá trị tương ứng của \(y\) thì \(y\) được gọi là hàm số của \(x.\)
Lời giải chi tiết
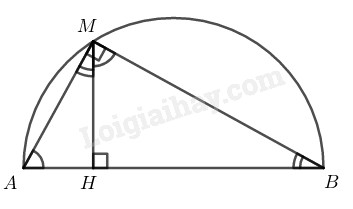
\(a)\) \(∆ AMB\) nội tiếp trong đường tròn có \(AB\) là đường kính nên \(\widehat {AMB} = 90^\circ \)
Suy ra: \(\widehat {MAB} + \widehat {MBA} = 90^\circ \) \( (1)\)
\(∆ AMH\) vuông tại \(H.\)
\(\widehat {MAH} + \widehat {HMA} = 90^\circ \)
hay \(\widehat {MAB} + \widehat {HMA} = 90^\circ \) \( (2)\)
Từ \((1)\) và \((2)\) suy ra: \(\widehat {MBA} = \widehat {HMA}\)
hay \(\widehat {MBH} = \widehat {HMA}\)
Xét \(∆ AHM\) và \(∆ MHB:\)
\(\widehat {AHM} = \widehat {MHB} = 90^\circ \)
\(\widehat {MBH} = \widehat {HMA}\)
Suy ra: \(∆ AHM\) đồng dạng \(∆ MHB\; (g.g)\)
\(b)\) \(∆ AHM\) đồng dạng \(∆ MHB\) (theo câu a)
Suy ra \(\displaystyle{{MH} \over {HA}} = {{HB} \over {HM}} \Rightarrow HA.HB = H{M^2}\)
\(c)\) Ta có: \(HA.HB = H{M^2}\) (theo câu b)
Suy ra \(P(x) = {x^2}\)
Với mỗi giá trị của \(x\) ta có một giá trị xác định của \(P(x).\)
Vậy \(P(x)=x^2\) là một hàm số.
dapandethi.vn
