Đề bài
Cho tam giác \(ABC\) có trung tuyến \(AM\). Trên cạnh \(AC\) lấy hai điểm \(E\) và \(F\) sao cho \(AE = EF= FC\); \(BE\) cắt \(AM \) tại \(N\). Chứng minh \(\overrightarrow {NA} \) và \(\overrightarrow {NM} \) là hai vec tơ đối nhau.
Phương pháp giải - Xem chi tiết
Ta chứng minh \(N\) là trung điểm của \(AM\) dựa vào đường trung bình của tam giác
Lời giải chi tiết
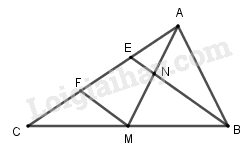
Xét tam giác \(CEB,\) ta có:
\(F\) là trung điểm \(CE \) (do \(CF = FE\) )
\(M\) là trung điểm \(CB \)
Suy ra \(FM // BE \) hay \(FM // EN \)
Lại có \(EA = EF\).
\( \Rightarrow EN\) là đường trung bình của tam giác \(AFM\).
Do đó \(N\) là trung điểm của \(AM\) và \(\overrightarrow {NA} = - \overrightarrow {NM} \).
dapandethi.vn
