Câu 1
Chơi trò chơi “Ghép thẻ” :
Ghép các thẻ tích hợp để được các phép tính đúng, chẳng hạn :
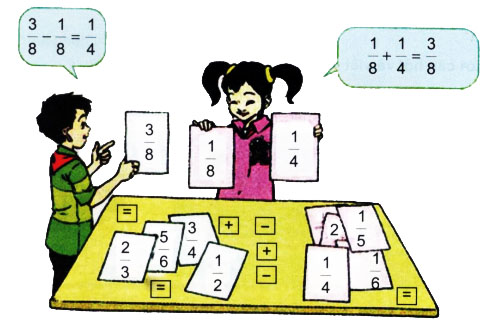
Ghi lại các phép tính nhóm em ghép được.
Nhóm nào ghép được nhiều phép tính đúng nhất là nhóm thắng cuộc.
Phương pháp giải:
- Các em tự tạo thẻ và chơi trò chơi theo nhóm.
- Áp dụng các quy tắc cộng (hoặc trừ) hai phân số :
+) Muốn cộng (hoặc trừ) hai phân số có cùng mẫu số, ta cộng (hoặc trừ) hai tử số với nhau và giữ nguyên mẫu số.
+) Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng (hoặc trừ) hai phân số đó.
Lời giải chi tiết:
Ví dụ :
\(\dfrac{1}{4} + \dfrac{1}{5} = \dfrac{9}{{20}}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{9}{{20}} - \dfrac{1}{4} = \dfrac{1}{5}\,;\,\) \(\dfrac{9}{{20}} - \dfrac{1}{5} = \dfrac{1}{4}\)
\(\dfrac{1}{2} + \dfrac{1}{6} = \dfrac{2}{3}\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{2}{3} - \dfrac{1}{2} = \dfrac{1}{6}\,\,;\) \(\dfrac{2}{3} - \dfrac{1}{6} = \dfrac{1}{2}.\)
\(\dfrac{3}{4} + \dfrac{1}{{12}} = \dfrac{5}{6}\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{5}{6} - \dfrac{3}{4} = \dfrac{1}{{12}}\,\,;\) \(\dfrac{5}{6} - \dfrac{1}{{12}} = \dfrac{3}{4}\,.\)
Câu 2
Tính:
\(a)\;\dfrac{{10}}{3} - \dfrac{8}{3};\,\,\,\,\,\,\,\dfrac{{11}}{4} - \dfrac{5}{4};\,\,\,\,\,\,\,\)\(\dfrac{{32}}{{17}} + \dfrac{{21}}{{17}}\)
\(b)\;\dfrac{{5}}{6} + \dfrac{7}{8};\,\,\,\,\,\,\,\dfrac{{3}}{7} - \dfrac{5}{14};\,\,\,\,\,\,\,\)\(\dfrac{{7}}{{4}} - \dfrac{{3}}{{5}}\)
Phương pháp giải:
Áp dụng các quy tắc cộng (hoặc trừ) hai phân số :
- Muốn cộng (hoặc trừ) hai phân số có cùng mẫu số, ta cộng (hoặc trừ) hai tử số với nhau và giữ nguyên mẫu số.
- Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng (hoặc trừ) hai phân số đó.
Lời giải chi tiết:
\(\begin{array}{*{20}{l}}
{a)\;\dfrac{{10}}{3} - \dfrac{8}{3} = \dfrac{{10 - 8}}{3} = \dfrac{2}{3}}\\
{\dfrac{{11}}{4} - \dfrac{5}{4} = \dfrac{{11 - 5}}{4} = \dfrac{6}{4} = \dfrac{3}{2}}\\
{\dfrac{{32}}{{17}} + \dfrac{{21}}{{17}} = \dfrac{{32 + 21}}{{17}} = \dfrac{{53}}{{17}}}
\end{array}\)
\(\begin{array}{*{20}{l}}
{b){\mkern 1mu} {\mkern 1mu} \dfrac{5}{6} + \dfrac{7}{8} = \dfrac{{20}}{{24}} + \dfrac{{21}}{{24}} = \dfrac{{41}}{{24}}}\\
{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \dfrac{3}{7} - \dfrac{5}{{14}} = \dfrac{6}{{14}} - \dfrac{5}{{14}} = \dfrac{1}{{14}}}\\
{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \dfrac{7}{4} - \dfrac{3}{5} = \dfrac{{35}}{{20}} - \dfrac{{12}}{{20}} = \dfrac{{23}}{{20}}}
\end{array}\)
Câu 3
Tính:
\(a)\;4 + \dfrac{1}{4};\,\,\,\,\,\) \(b)\;\dfrac{7}{6} - 1;\,\,\,\,\,\) \(c)\;7 - \dfrac{8}{5};\,\,\,\,\,\) \(d)\;\dfrac{3}{4} + 5\)
Phương pháp giải:
Viết số tự nhiên dưới dạng phân số có mẫu số là \(1\) , sau đó thực hiện phép cộng (hoặc phép trừ) hai phân số như thông thường.
Lời giải chi tiết:
\(\begin{array}{*{20}{l}}
{a)\,4 + \dfrac{1}{4} = \dfrac{4}{1} + \dfrac{1}{4} = \dfrac{16}{4} + \dfrac{1}{4} = \dfrac{17}{4}}\\
{b)\,\dfrac{7}{6} - 1 = \dfrac{7}{6} - \dfrac{1}{1} = \dfrac{7}{6} - \dfrac{6}{6} = \dfrac{1}{6}}\\
{c)\,7 - \dfrac{8}{5} = \dfrac{7}{1} - \dfrac{8}{5} = \dfrac{{35}}{5} - \dfrac{8}{5} = \dfrac{{27}}{5}}\\
{d)\,\dfrac{3}{4} + 5 = \dfrac{3}{4} + \dfrac{5}{1} = \dfrac{3}{4} + \dfrac{{20}}{4} = \dfrac{{23}}{4}}
\end{array}\)
Câu 4
Tìm \(x\):
\(a)\; x + \dfrac{4}{5} = \dfrac{7}{5}\) \(b)\;x - \dfrac{4}{3} = \dfrac{7}{4}\)
\(c)\; \dfrac{7}{4} - x = \dfrac{3}{{14}}\)
Phương pháp giải:
Áp dụng các quy tắc :
- Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.
- Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ.
- Muốn tìm số trừ ta lấy số bị trừ trừ đi số trừ.
Lời giải chi tiết:
\(\begin{array}{*{20}{l}}
{a)\;x + \dfrac{4}{5} = \dfrac{7}{5}}\\
{\;\;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x = \dfrac{7}{5} - \dfrac{4}{5}}\\
{\;\;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x = \dfrac{3}{5}}\\
{b)\;x - \dfrac{4}{3} = \dfrac{7}{4}}\\
{\;\;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x = \dfrac{7}{4} + \dfrac{4}{3}}\\
{\;\;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x = \dfrac{{37}}{{12}}}\\
{c)\;\dfrac{4}{7} - x = \dfrac{3}{{14}}}\\
{\;\;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x = \dfrac{4}{7} - \dfrac{3}{{14}}}\\
{\;\;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x = \dfrac{5}{{14}}}
\end{array}\)
Câu 5
Có một đàn trâu, bò và ngựa đang ăn cỏ. Số trâu chiếm \(\dfrac{1}{3}\) đàn, số ngựa chiếm \(\dfrac{1}{2}\) đàn. Hỏi số bò chiếm mấy phần của cả đàn ?
Phương pháp giải:
- Tìm phân số chỉ số trâu và số ngựa so với cả đàn.
- Coi cả đàn là \(1\) đơn vị, để tìm phân số chỉ số bò so với cả đàn ta lấy \(1) trừ đi phân số chỉ số trâu và số ngựa so với cả đàn.
Lời giải chi tiết:
Số trâu và số ngựa chiếm số phần của cả đàn là :
\(\dfrac{1}{3} + \dfrac{1}{2} = \dfrac{5}{6}\) (đàn)
Số bò chiếm số phần cả đàn là :
\(1 - \dfrac{5}{6} = \dfrac{1}{6}\) (đàn)
Đáp số: \(\dfrac{1}{6}\) đàn.
dapandethi.vn
