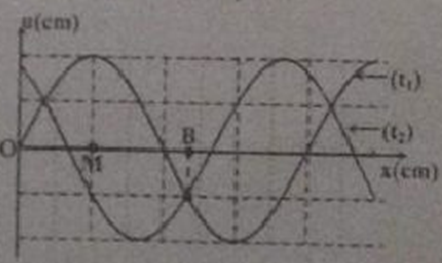Câu hỏi 1 :
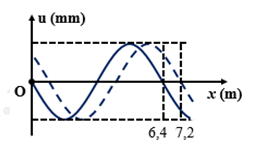
Cho một sợi dây cao su căng ngang. Làm cho đầu O của dây dao động theo phương thẳng đứng. Hình vẽ mô tả hình dạng sợi dây tại thời điểm t1 (đường nét liền) và t2= t1 + 0,2s (đường nét đứt). Tại thời điểm t3 = t2 + 0,4s thì độ lớn li độ của phần tử M cách đầu dây một đoạn 2,4m (tính theo phương truyền sóng) là \(\sqrt 3 cm\). Gọi δ là tỉ số của tốc độ cực đại của phần tử trên dây với tốc độ truyền sóng. Giá trị của δ gần giá trị nào nhất sau đây?
- A 0,025.
- B 0,022.
- C 0,012.
- D 0,018.
Đáp án: D
Phương pháp giải:
Sử dụng lí thuyết về sự truyền sóng, vòng tròn lượng giác và kĩ năng đọc đồ thị.
Lời giải chi tiết:
Từ đồ thị ta có: \(\lambda =6,4m\)
Vận tốc truyền sóng : \(v=\frac{\Delta {{x}_{12}}}{\Delta {{t}_{12}}}=\frac{7,2-6,4}{0,2}=4m/s\)
Tần số góc dao động của các phần tử :
\(\omega =\frac{2\pi }{T}=\frac{2\pi }{\frac{\lambda }{v}}=\frac{2\pi .v}{\lambda }=\frac{2\pi .4}{6,4}=\frac{5\pi }{4}rad/s\)
Độ lệch pha giữa M và O:
\(\begin{gathered}
\Delta \varphi = \Delta {\varphi _x} + \Delta {\varphi _t} = \frac{{2\pi .\Delta {x_{13}}}}{\lambda } + \omega .\Delta {t_{13}} \hfill \\
\,\,\,\,\,\,\,\,\, = \frac{{2\pi .2,4}}{{6,4}} + \frac{{5\pi }}{4}\left( {0,2 + 0,4} \right) = \frac{{3\pi }}{2}rad \hfill \\
\end{gathered} \)
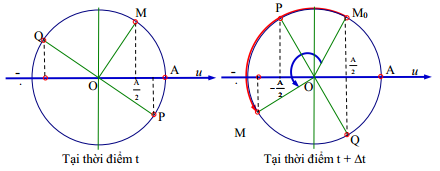
Biểu diễn trên VTLG:
Từ VTLG ta có:
\({{u}_{M}}=a=\sqrt{3}cm\Rightarrow \delta =\frac{\omega A}{v}=\frac{\frac{5\pi }{4}.\sqrt{3}{{.10}^{-2}}}{4}=0,017\)
Chọn D.
Câu hỏi 2 :
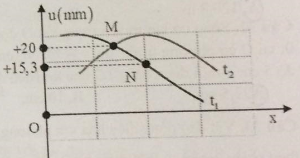
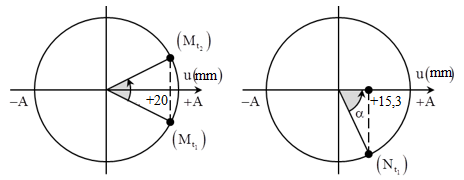
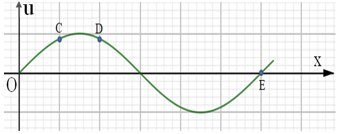
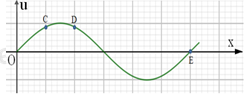
Trên một sợi dây dài có một sóng ngang, hình sin truyền qua.Hình dạng của một đoạn dây tại hai thời điểm t1 và t2 có hình dạng như hình vẽ bên.
Trục Ou biểu diễn các phần tử M và N ở các thời điểm. Biết t2 – t1 bằng 0,05s, nhỏ hơn 1 chu kỳ sóng. Tốc độ cực đại của một phần tử trên dây bằng
- A 34 cm/s
- B 3,4 m/s
- C 4,25 m/s
- D 42,5 cm/s
Đáp án: C
Phương pháp giải:
Sử dụng vòng tròn lượng giác
Lời giải chi tiết:
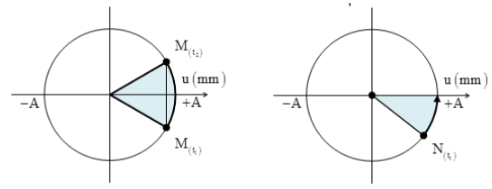
Từ hình vẽ ta xác định được:
Tại t1:
\(\left\{ \matrix{ {u_M} = 20mm \hfill \cr {u_N} = 15,4mm \hfill \cr} \right.\)
Tại t2:
\(\left\{ \matrix{ {u_M} = 20mm \hfill \cr {u_N} = + Amm \hfill \cr} \right.\)
Ta có:
\(\left\{ \matrix{ {\rm{cos}}{\alpha \over 2} = {{20} \over A} \hfill \cr {\rm{cos}}\alpha {\rm{ = }}{{{\rm{15}}{\rm{,3}}} \over A}{\rm{ = 2co}}{{\rm{s}}^2}\left( {{\alpha \over 2}} \right) - 1 \hfill \cr} \right. \to {{{\rm{15}}{\rm{,3}}} \over A} = 2.{({{20} \over A})^2} - 1 \to {1 \over A} = 0,0462 \to A = 21,6mm\)
\(\omega = 5\pi {\rm{r}}a{\rm{d}}/s \to {v_{{\rm{max}}}} = A\omega = 21,6.5\pi \approx 340mm/s = 34cm/s\)
=> Đáp án C
Câu hỏi 3 :
Một sóng cơ lan truyền trên sợi dây từ C đến B với chu kì T = 2 s, biên độ không đổi. Ở thời điểm t0, ly độ các phần tử tại B và C tương ứng là – 20 mm và + 20 mm, các phần tử tại trung điểm D của BC đang ở vị trí cân bằng. Ở thời điểm t1, li độ các phần tử tại B và C cùng là +8 mm. Tại thời điểm t2 = t1 + 0,4 s thì tốc độ dao động của phần tử D có giá trị gần nhất với giá trị nào sau đây:
- A 64,36 mm/s.
- B 67,67 mm/s.
- C 58,61 mm/s.
- D 33,84 mm/s.
Đáp án: C
Phương pháp giải:
Phương trình dao động của hai chất điểm :
Lời giải chi tiết:
Đáp án C
Phương trình dao động của hai chất điểm :
\({{\rm{x}}_1} = A\cos \left( {\omega t - {\pi \over 2}} \right)\) và \({{\rm{x}}_2} = A\cos \left( {{\omega \over 2}t - {\pi \over 2}} \right)\)
Mặt khác \({v_{2\max }} = {\omega \over 2}A \Rightarrow \omega = \pi \,\,{{rad} /s}.\)
Hai chất điểm này gặp nhau
\({{\rm{x}}_1} = {x_2} \Rightarrow \cos \left( {\pi t - {\pi \over 2}} \right) = \cos \left( {{\pi \over 2}t - {\pi \over 2}} \right) \Leftrightarrow \left[ \matrix{
\pi t - {\pi \over 2} = {\pi \over 2}t - {\pi \over 2} + 2k\pi \hfill \cr
\pi t - {\pi \over 2} = - {\pi \over 2}t + {\pi \over 2} + 2k\pi \hfill \cr} \right.\)
+ Với nghiệm thứ nhất \( \Rightarrow {t_1} = 4k\)
+ Với nghiệm thứ hai \( \Rightarrow {t_2} = {2 \over 3}\left( {2k + 1} \right)\)
Các thời điểm gặp nhau
lần gặp thứ 5 ứng với \(t = 4,67\,\,s\,.\)
Câu hỏi 4 :
Một sóng cơ lan truyền dọc theo trục Ox trên một sợi dây đàn hồi tần số f = 1/6 (Hz). Tỉ số giữa tốc độ dao động cực đại của phần tử dây và tốc độ truyền sóng có giá trị 8π/3 (cm/s). Tại thời điêmt t0 = 0 và thời điểm t1 hình ảnh sợi dây có dạng như hình vẽ. Biết d2 – d1 = 4cm. Thời điểm t1 có giá trị là
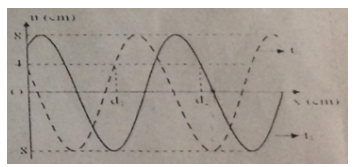
- A 3s
- B 2s
- C 1,75s
- D 0,5s
Đáp án: B
Lời giải chi tiết:
Đáp án B
Câu hỏi 5 :
Một sóng ngang có chu kì T (T > 4/15s), truyền trên mặt nước, dọc theo chiều dương trục Ox với vận tốc v = 240cm/s. Tại thời điểm t1 và \({t_2} = {t_1} + {4 \over {15}}(s)\) dạng mặt nước như hình vẽ. Trên mặt nước, hai điểm M, B là vị trí cân bằng của phần tử môi trường. Khoảng cách giữa hai điểm M, B là:
- A d = 44cm
- B d = 32cm
- C d = 36cm
- D d = 40cm
Đáp án: B
Phương pháp giải:
Sử dụng kĩ năng đọc đồ thì và công thức tính độ lệch pha \(\Delta \varphi = {{2\pi d} \over \lambda }\)
Lời giải chi tiết:
+ Xét điểm B tại hai thời điểm t1 và t2 thấy: B đi qua vị trí \(x = {{ - A} \over 2}\) và ngược chiều nhau, suy ra:
\({t_2} - {t_1} = {{2T} \over 3} = {4 \over {15}} \to T = 0,4s \to \lambda = 96cm\)
+ Tại thời điểm t2 thì M và B cùng li độ \(x = {{ - A} \over 2}\) suy ra độ lệch pha giữa hai điểm là: \(\Delta \varphi = {{2\pi d} \over \lambda } = {{2\pi } \over 3} \to d = {\lambda \over 3} = 32cm\)
Câu hỏi 6 :
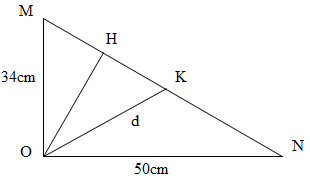
Một nguồn sóng đặt tại điểm O trên mặt nước, dao động theo phương vuông góc với mặt nước với phương trình u = acos40πt (cm), trong đó t tính theo giây. Gọi M và N là hai điểm nằm trên mặt nước sao cho OM vuông góc với ON. Biết tốc độ truyền sóng trên mặt nước bằng 80cm/s. Khoảng cách từ O đến M và N lần lượt là 34cm và 50cm. Số phần tử trên đoạn MN dao động cùng pha với nguồn là
- A 5
- B 7
- C 6
- D 4
Đáp án: C
Phương pháp giải:
Độ lệch pha: \(\Delta \varphi = {{2\pi d} \over \lambda }\)
Lời giải chi tiết:
+ Áp dụng hệ thức lượng trong tam giác vuông OMN có đường cao OH:
\({1 \over {O{H^2}}} = {1 \over {O{M^2}}} + {1 \over {O{N^2}}} \Leftrightarrow {1 \over {O{H^2}}} = {1 \over {{{34}^2}}} + {1 \over {{{50}^2}}} \Rightarrow OH = 28,1cm\)
+ Gọi d là khoảng cách từ O đến K (K là 1 điểm bất kì trên MN)
+ Độ lệch pha giữa K và O là : \(\Delta \varphi = {{2\pi d} \over \lambda }\)
+ Để K dao động cùng pha với O thì : \(\Delta \varphi = {{2\pi d} \over \lambda } = 2k\pi \Rightarrow d = k\lambda \)
+ Số điểm dao động cùng pha với o trên đoạn MN bằng số giá trị k nguyên thoả mãn :
\(\left\{ \matrix{
28,1 \le k\lambda \le 34 \Rightarrow 7,025 \le k \le 8,5 \Rightarrow k = 8 \hfill \cr
28,1 < k\lambda \le 50 \Rightarrow 7,025 < k \le 12,5 \Rightarrow k = 8;9;10;11;12 \hfill \cr} \right.\)
Có 6 giá trị của k thoả mãn => trên đoạn MN có 6 điểm dao động cùng pha với nguồn
Câu hỏi 7 :
Sóng cơ lan truyền qua điểm M rồi đến điểm N cùng nằm trên một phương truyền sóng. Bước sóng bằng 40cm. Khoảng cách MN bằng 90cm. Coi biên độ sóng không đổi trong quá trình truyền sóng. Tại một thời điểm nào đó phần tử vật chất tại M đang có li độ 2cm thì phần tử vật chất tại N có tốc độ 125,6cm/s. Sóng có tần số bằng
- A 12Hz
- B 18Hz
- C 10Hz
- D 15Hz
Đáp án: C
Phương pháp giải:
Phương trình của li độ và vận tốc:
\(\left\{ \matrix{
u = A\cos \left( {\omega t + \varphi } \right) \hfill \cr
v = \omega Ac{\rm{os}}\left( {\omega t + \varphi + {\pi \over 2}} \right) \hfill \cr} \right.\)
Lời giải chi tiết:
Độ lệch pha giữa M và N: \(\Delta \varphi = {{2\pi .MN} \over \lambda } = {{2\pi .90} \over {40}} = 4,5\pi \)
Phương trình li độ và vận tốc tại M và N:
\(\left\{ \matrix{
{u_M} = A\cos \left( {\omega t + \varphi } \right) \hfill \cr
{v_M} = \omega Ac{\rm{os}}\left( {\omega t + \varphi + {\pi \over 2}} \right) \hfill \cr
{u_N} = A\cos \left( {\omega t + \varphi + 4,5\pi } \right) \hfill \cr
{v_N} = \omega Ac{\rm{os}}\left( {\omega t + \varphi + {\pi \over 2} + 4,5\pi } \right) = \omega Ac{\rm{os}}\left( {\omega t + \varphi + 5\pi } \right) = - \omega Ac{\rm{os}}\left( {\omega t + \varphi } \right) \hfill \cr} \right.\)
Tại thời điểm t thì:
\(\left\{ \matrix{
{u_M} = A\cos \left( {\omega t + \varphi } \right) = 2cm \hfill \cr
{v_N} = \left| { - \omega Ac{\rm{os}}\left( {\omega t + \varphi } \right)} \right| = 125,6cm \hfill \cr} \right. \Rightarrow {{{v_N}} \over {{u_M}}} = \omega = {{125,6} \over 2} = 62,8 = 2\pi f \Rightarrow f = 10Hz\)
Câu hỏi 8 :
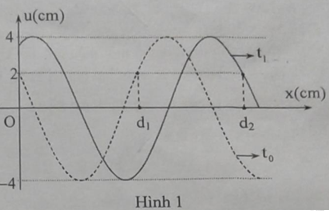
Cho một sóng cơ truyền dọc theo trục Ox trên một sợi dây đàn hồi rất dài chu ỳ 6s. Tại thời điểm t0 = 0 và thời điểm t1 = 1,75s, hình dạng sợi dây như hình 1. Biết d2 – d1 = 3cm. Tỉ số giữa tốc độ dao đọng cự đại của phần tử trên dây và tốc độ truyền sóng là
- A 2π
- B \(\frac{{5\pi }}{3}\)
- C \(\frac{{5\pi }}{8}\)
- D \(\frac{{3\pi }}{4}\)
Đáp án: B
Lời giải chi tiết:
Đáp án B
Ta có \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{6} = \frac{\pi }{3}(rad/s)\)
Gọi s là quãng đường sóng truyền được trong thời gian 1,75s
Từ hình vẽ ta có \(\frac{\lambda }{6} + s + \frac{\lambda }{6} = 3\)
Mặt khác ta có\(t = 1,75s = \frac{{7T}}{{24}} = > s = \frac{{7\lambda }}{{24}} = > \frac{\lambda }{6} + \frac{{7\lambda }}{{24}} + \frac{\lambda }{6} = 3 = > \lambda = 4,8cm\)
Tốc độ truyền sóng là \(v = \frac{\lambda }{T} = \frac{{4,8}}{6} = 0,8(cm/s)\)
Tốc độ dao động cực đại là\({v_{max}} = \omega A = \frac{\pi }{3}.4 = \frac{{4\pi }}{3}(cm/s)\)
Tỷ số giữa tốc độ dao động cực đại và tốc độ truyền sóng trên dây là \(\frac{{\frac{{4\pi }}{3}}}{{0,8}} = \frac{{5\pi }}{3}\)
Câu hỏi 9 :
Sóng ngang có tần số f truyền trên một sợi dây đàn hồi rất dài, với tốc độ 3 m/s. xét hai điểm M và N nằm trên cùng một phương truyền sóng, cách nhau một khoảng x. Đồ thị biểu diễn li độ sóng của M và N cùng theo thời gian như hình vẽ. Biết t1 = 0,05s. Tại thời điểm t2 khoảng cách giữa hai phần tử chất lỏng tại M, N có giá trị gần nhất với giá trị nào sau đây:
- A \(\sqrt {19} cm\)
- B \(\sqrt {18} cm\)
- C \(\sqrt {21} cm\)
- D \(\sqrt {20} cm\)
Đáp án: C
Phương pháp giải:
viết phương trình dao động của M và N; tính khoảng cách giữa M, N từ x và tọa độ M, N tại thời điểm t2
Lời giải chi tiết:
Thời điểm ban đầu t = 0 thì phần tử N ở biên dương, nên pha ban đầu là 0
Ta có phương trình dao động của N là uN = 4.cos (ωt) (cm)
Thời điểm ban đầu phần tử M ở vị trí x0= +2 và chuyển động theo chiều dương=> pha ban đầu là \(\frac{{ - \pi }}{3}\)
Ta có phương trình dao động của M là
\({u_M} = 4.\cos \left( {\omega t - \frac{\pi }{3}} \right)cm\)
Sóng truyền từ M đến N, ta có thể có:
\(\frac{{\omega .x}}{v} = \frac{\pi }{3} = > x = \frac{v}{{3.2.f}} = \frac{{v.T}}{6} = \frac{{10}}{3}cm\)
Biên độ của N và M là 4, nên tính từ thời điểm ban đầu đến t1 thì N đi từ biên dướng đến vị trí cân bằng lần 2. Tức là hết ¾.T => T = 4/3.0,05s
Xét phần tử N, từ thời điểm ban đầu đến vị trí t2
Tổng thời gian là:
\(\frac{T}{6} + T + \frac{T}{4} = \frac{{17}}{{12}}.T\)
Vậy t2= \(\frac{{17}}{{12}}.T\)
Thay vào phương trình dao động của N tìm được tọa độ của N tại thời điểm t2 là
UN= \( - 2\sqrt 3 cm\)
Khoảng cách của M và N tại thời điểm t2 là :
\(\Delta d = \sqrt {{x^2} + {{({u_M} - {u_N})}^2}} = \sqrt {{{(\frac{{10}}{3})}^2} + {{\left( {2\sqrt 3 } \right)}^2}} = \sqrt {23} cm\)
Vậy gần nhất với đáp án C
Câu hỏi 10 :
Một sóng cơ truyền trên một sợi dây rất dài từ một đầu dây với biên độ không đổi là 4 mm, tốc độ truyền sóng trên dây là 2,4 m/s, tần số sóng là 20 Hz. Hai điểm M và N trên dây cách nhau 37 cm, sóng truyền từ M đến N. Tại thời điểm t, sóng tại M có li độ -2 mm và M đang đi về vị trí cân bằng. Vận tốc dao động của điểm N ở thời điểm (t -\({{89} \over {80}}\) ) s là
- A 16π cm/s.
- B \(- 8\sqrt 3 \pi {\rm{ }}cm/s.\)
- C \(80\sqrt 3 \pi {\rm{ }}mm/s.\)
- D -8π cm/s.
Đáp án: B
Lời giải chi tiết:
Đáp án B
Ta có : \(\lambda = {v \over f} = 12cm = > MN = 37cm = 3\lambda + {\lambda \over {12}}\)
Vì sóng tuần hoàn theo không gian nên sau điểm M đoạn 3λ có điểm M’ có tính chất như điểm M
nên ở thời điểm t điểm M’ cũng có li độ uM’= -2 mm và đang đi về VTCB.
Vì \({u_{M'}} = - 2mm = - {A \over 2} = > {x_{M'}} = {\lambda \over {12}}\)
Vì N cách M’ đoạn \({\lambda \over {12}} = > {x_N} = {\lambda \over 6}\)
Ta có : \(\Delta t = {{89} \over {80}}s = 22T + {T \over 4}\)=> lùi về quá khứ \({T \over 4}\)=> điểm N có li độ \({x_N} = - {A \over 2}\)
\({v_N} = - {{\omega A\sqrt 3 } \over 2} = - 80\pi \sqrt 3 (mm/s)\)
Câu hỏi 11 :
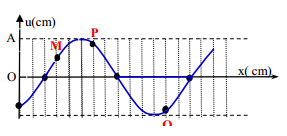
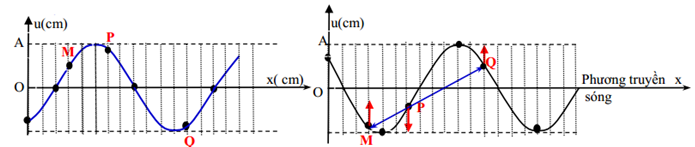
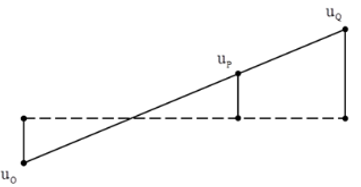
Một sợi dây đàn hồi đủ dài đang có sóng ngang hình sin truyền qua theo chiều dương của trục Ox, với tần số sóng f = 1 Hz. Ở thời điểm t, một đoạn của sợi dây và vị trí của ba điểm M, P, Q trên đoạn dây này như hình vẽ. Giả sử ở thời điểm t + Δt, ba điểm M, P, Q thẳng hàng. Giá trị nhỏ nhất của Δt gần nhất với kết quả nào sau đây?
- A 0,51 s.
- B 0,41 s.
- C 0,72 s.
- D 0,24 s.
Đáp án: B
Lời giải chi tiết:
Đáp án B
Nhìn vào đồ thị ta thấy: Mỗi ô là λ/12 ứng với T/12.M nhanh pha hơn P góc π/2 ( M vuông pha với P).P nhanh pha hơn Q góc π ( Q ngược pha với P).
+Ở thời điểm t: ( Hình vẽ )
\({u_M} = \frac{A}{2};{u_P} = \frac{{A\sqrt 3 }}{2};{u_Q} = - \frac{{A\sqrt 3 }}{2}\)
+Ở thời điểm t +Δt: 3 điểm thẳng hàng. \({u_M} = - \frac{{A\sqrt 3 }}{2};{u_P} = - \frac{A}{2};{u_Q} = \frac{A}{2}\)
Nhìn vào vòng tròn lượng giác ta thấy:
Góc quay là M0OM = π/6 + π/2 + π/6 = 5π/6 => ứng với thời gian quay nhỏ nhất là 5T/12.
Vị trí của ba điểm M, P, Q sau thời gian 5T/12 là thẳng hàng.
Với chu kì T =1 s nên thời gian nhỏ nhất cần tìm là: Δt = 5/12 s = 0,41667 s .Vậy chọn đáp án B.
Câu hỏi 12 :
Một dây đàn hồi rất dài có đầu O dao động với tần số f theo phương vuông góc với dây. Tốc độ truyền sóng trên dây là 5m/s. Xét một điểm M trên dây cách O một khoảng 25 cm, người ta thấy M luôn dao động vuông pha với O. Biết tần số f có giá trị từ 23 Hz đến 33 Hz. Bước sóng trên dây có giá trị:
- A 20 cm.
- B 25 cm.
- C 10 cm.
- D 15 cm.
Đáp án: A
Phương pháp giải:
Áp dụng công thức tổng quát của sóng trên dây \(u = a.\cos \left( {\omega t - \frac{{2\pi d}}{\lambda }} \right)\)
và độ lệch pha của hai điểm trên cùng một phương truyền sóng
\(\Delta \varphi = 2\pi \frac{{\Delta d}}{\lambda }\)
, công thức tính bước sóng λ = v/ f
Lời giải chi tiết:
Phương trình sóng tổng quát là\(u = a.\cos \left( {\omega t - \frac{{2\pi d}}{\lambda }} \right)\)
Điểm M cách nguồn 25 cm luôn dao động vuông pha với nguồn nên
\(\begin{array}{l}
\Delta \varphi = 2\pi .\frac{{{d_M}}}{\lambda } = \frac{\pi }{2} + k\pi \Leftrightarrow \frac{{2.{d_M}}}{{\frac{v}{f}}} = \frac{1}{2} + k\\
\Leftrightarrow \frac{{2.25.f}}{{500}} = \frac{1}{2} + k\\
\Leftrightarrow f = 5 + 10k
\end{array}\)
Vì f có giá trị từ 23 Hz đến 33 Hz nên 23 ≤ 5+10k ≤ 33
=> k = 2 nên f = 25 Hz
Vậy bước sóng là λ = v/ f = 500/25 = 20 cm.
Câu hỏi 13 :
Sóng cơ lan truyền trên sợi dây, qua hai điểm M và N cách nhau 100cm. Dao động tại M sớm pha hơn dao động tại N là \(\frac{\pi }{3}+k\pi \) (k=0,1,2...). Giữa M và N chỉ có 4 điểm mà dao động tại đó lệch pha \(\frac{\pi }{2}\) so với dao động tại M. Biết tần số sóng bằng 20Hz . Tốc độ truyền sóng trên dây gần nhất với giá trị
- A 1090cm/s
- B 800cm/s
- C 900cm/s
- D 925cm/s
Đáp án: D
Lời giải chi tiết:
Ta có \(MN = 100cm;\Delta {\varphi _{MN}} = \frac{\pi }{3} + k\pi = 2\pi .\frac{{MN}}{\lambda } = > MN = \frac{\lambda }{6} = k\frac{\lambda }{2}\)
Gọi X là điểm vuông pha với M \( = > XM = \left( {\frac{{k'}}{2} + \frac{1}{4}} \right)\lambda \)
Trên MN có 4 điểm X nên \(XM = \frac{\lambda }{4};\frac{{3\lambda }}{4};\frac{{5\lambda }}{4};\frac{{7\lambda }}{4}\)
\(\begin{array}{l}MN > \frac{{7\lambda }}{4} = > \frac{\lambda }{6} + k\frac{\lambda }{2} > \frac{{7\lambda }}{4} = > k > 3,16 = > k = 4\\MN = \frac{\lambda }{6} + \frac{{4\lambda }}{2} = \frac{{13\lambda }}{6} = 100 = > \lambda = \frac{{600}}{{13}} = > v = \lambda f = 923,07\end{array}\)
Chọn D
Câu hỏi 14 :
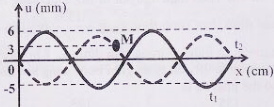
Trên sợi dây căng ngang dài 40cm, hai đầu cố định đang có sóng dừng với tần số f xác định. Hình vẽ bên mô tả hình dạng sợi dây ở thời điểm t1 và thời điểm \({t_2} = {t_1} + \frac{1}{{6f}}\). Tỉ số giữa tốc độ truyền sóng trên dây và tốc độ dao động cực đại của điểm M xấp xỉ bằng
- A 4,2
- B 6,9
- C 5,8
- D 4,8
Đáp án: D
Phương pháp giải:
Phương pháp : Sử dụng vòng tròn lượng giác trong truyền sóng cơ
Lời giải chi tiết:
Cách giải :
Theo bài ra ta có \(\left\{ \begin{array}{l}l = 4\frac{\lambda }{2} = 40cm = > \lambda = 20cm\\\Delta t = {t_2} - {t_1} = \frac{1}{{6f}} = \frac{T}{6}\end{array} \right.\)
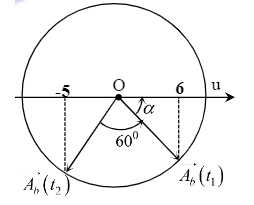
\(\left\{ \begin{array}{l}6 = {A_b}\cos \alpha \\5 = {A_b}\cos \left( {120 - \alpha } \right)\end{array} \right. = > {A_b} = 11cm\)
\(\left\{ \begin{array}{l}\frac{{{u_M}}}{{{u_B}}} = - \frac{{{A_M}}}{{{A_b}}} = > {A_M} = - {A_b}\frac{{{u_M}}}{{{u_B}}} = - 12\frac{3}{{ - 5}} = 6,6mm\\\delta = \frac{v}{{{v_{max}}}} = \frac{{\frac{\lambda }{T}}}{{{A_b}\frac{{2\pi }}{T}}} = \frac{\lambda }{{2\pi {A_b}}} = \frac{{200}}{{2\pi .7,2}} \approx 4,8\end{array} \right.\)
Chọn D
Câu hỏi 15 :
Ở mặt nước, một nguồn sóng đặt tại điểm O dao động điều hòa theo phương thẳng đứng. Sóng truyền trên mặt nước có bước sóng λ. Chọn hệ tọa độ vuông góc Oxy (thuộc mặt nước). Hai điểm P và Q nằm trên Ox, P dao động ngược pha với O còn Q dao động cùng pha với O. Giữa khoảng OP có 4 điểm dao động ngược pha với O, giữa khoảng OQ có 8 điểm dao động ngược pha với O. Trên trục Oy có điểm M sao cho góc  PMQ đạt giá trị lớn nhất. Tìm số điểm dao động ngươc pha với O trên đoan MQ
PMQ đạt giá trị lớn nhất. Tìm số điểm dao động ngươc pha với O trên đoan MQ
- A 5.
- B 4.
- C 6.
- D 7.
Đáp án: B
Phương pháp giải:
Giao thoa sóng, định lí hàm số sin, bất đẳng thức Bu-nhi-a-cốp-xki.
Lời giải chi tiết:
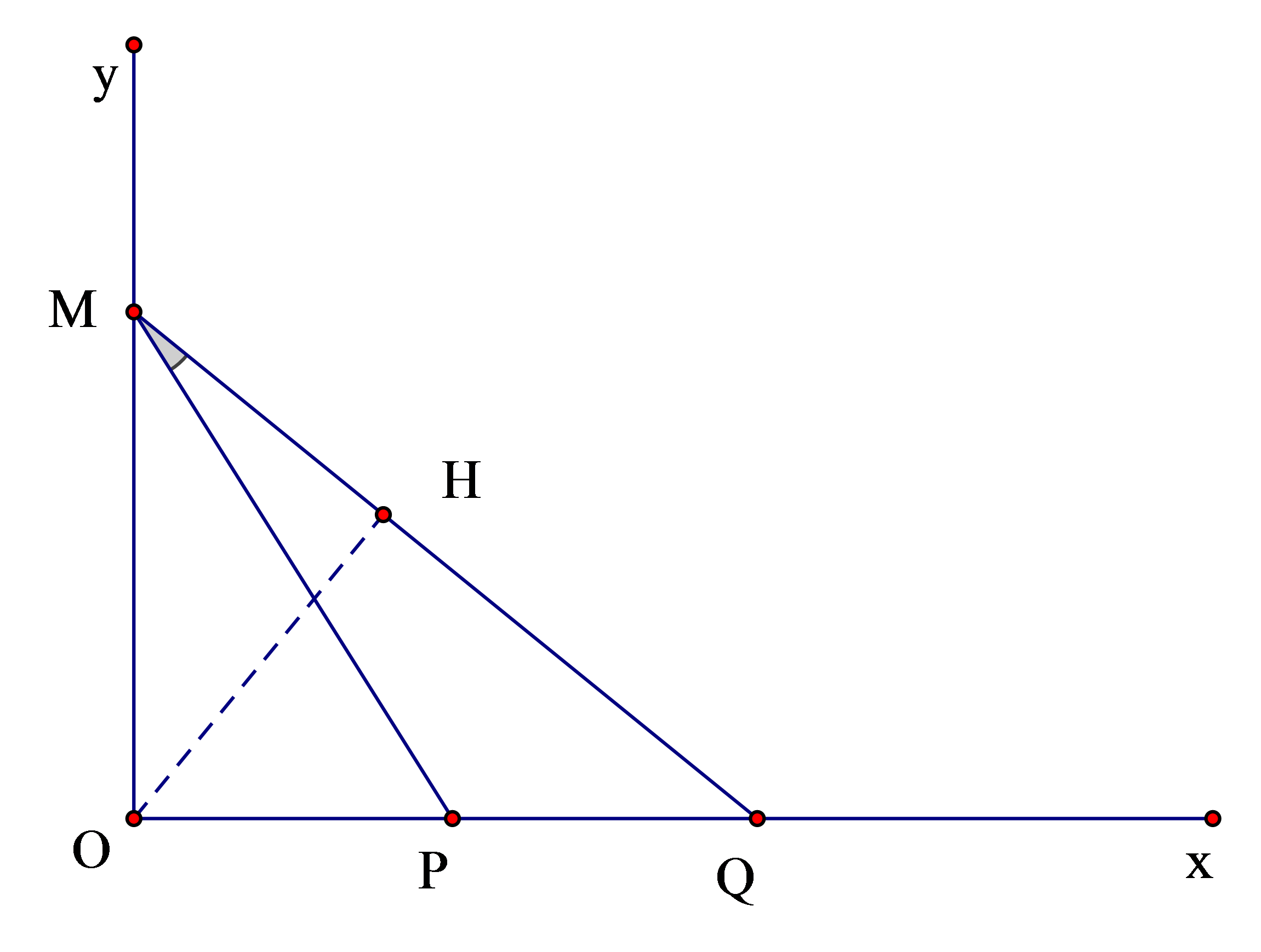
Theo đề bài ta suy ra: OP = 4,5λ, OQ = 8λ
Áp dụng định lí hàm số sin trong tam giác MPQ ta có
\({{PQ} \over {\sin PMQ}} = {{MP} \over {\sin MQP}} = {{\sqrt {O{M^2} + O{P^2}} } \over {{{OM} \over {\sqrt {O{M^2} + O{Q^2}} }}}} = {{\sqrt {\left( {O{M^2} + O{P^2}} \right)\left( {O{M^2} + O{Q^2}} \right)} } \over {OM}}\)
Đặt OM = x ta có \({{PQ} \over {\sin PMQ}} = {{\sqrt {\left( {{x^2} + O{P^2}} \right)\left( {{x^2} + O{Q^2}} \right)} } \over x}\)
Áp dụng bất đẳng thức Bu-nhi-a-cốp-xki cho tích \(\left( {{x^2} + O{P^2}} \right)\left( {{x^2} + O{Q^2}} \right) \ge {\left( {OPx + OQx} \right)^2}\)
Do đó, \({{PQ} \over {\sin PMQ}} = {{\sqrt {\left( {{x^2} + O{P^2}} \right)\left( {{x^2} + O{Q^2}} \right)} } \over x} \ge {{x\left( {OP + OQ} \right)} \over x} = OP + OQ = 12,5\lambda \Rightarrow \sin PMQ \le {{3,5} \over {12,5}}\)
Dấu “=” xảy ra ứng với góc PMQ lớn nhất khi \({{OP} \over x} = {x \over {OQ}} \Leftrightarrow x = \sqrt {OP.OQ} = 6\lambda \)
Do đó, OM = 6λ
* Tìm số điểm dao động ngược pha với O trên đoạn MQ
Ta tính được OH = 4,8λ
- Số điểm dao động ngược pha với nguồn trên đoạn HM là số giá trị nguyên của k thỏa mãn
\(4,8\lambda \le d = \left( {k + {1 \over 2}} \right)\lambda \le 6\lambda \Rightarrow \le 4,3 \le k \le 5,5 \Rightarrow k = 5\)
Trên đoạn HM có 1 điểm
- Số điểm dao động ngược pha với nguồn trên đoạn HQ là số giá trị nguyên của k thỏa mãn
\(4,8\lambda \le d = \left( {k + {1 \over 2}} \right)\lambda \le 8\lambda \Rightarrow \le 4,3 \le k \le 7,5 \Rightarrow k = 5,6,7\)
Trên đoạn HQ có 3 điểm
Vậy trên MQ có 4 điểm dao động ngược pha với O
→ Chọn B
Câu hỏi 16 :
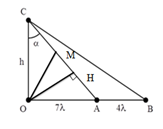
Một sóng hình sin lan truyền trên mặt nước từ nguồn O với bước sóng λ. Ba điểm A, B, C trên hai phương truyền sóng sao cho OA luôn vuông góc với OC và B là một điểm thuộc tia OA sao cho OB > OA. Biết OA = 7λ. Tại một thời điểm người ta quan sát thấy giữa A và B có 5 đỉnh sóng (kể cả A và B). Di chuyển điểm C sao cho góc ACB đạt giá trị lớn nhất thì số điểm dao động ngược pha với nguồn trên đoạn AC lúc này bằng
- A 7
- B 5
- C 6
- D 4
Đáp án: C
Phương pháp giải:
Sử dụng giản đồ vecto và kĩ năng đọc đồ thị
Áp dụng định lí hàm số sin trong tam giác và tính chất dãy tỉ số bằng nhau.
Công thức lượng giác: \(\sin a + \sin b = 2\sin \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}\)
Áp dụng công thức lượng giác: $\tan (a - b) = \frac{{\tan a - \tan b}}{{1 + \tan a.\tan b}}$
- Bất đẳng thức Cô – si :\(a + b \ge 2\sqrt {ab} \) Dấu ‘’=’’ xảy ra khi a = b
Lời giải chi tiết:
Khi điểm M dao động ngược pha với nguồn:${{d}_{M}}=(2k+1)\frac{\lambda }{2}$
Giữa A và B có 5 đỉnh sóng với A,B cũng là đỉnh sóng:$ \Rightarrow AB = 4\lambda $
Ta có:
$\left\{ \begin{array}{l}
\tan \alpha = \frac{{OA}}{{OC}} = \frac{{7\lambda }}{h}\\
\tan \widehat {OCB} = \frac{{OB}}{{OC}} = \frac{{11\lambda }}{h}
\end{array} \right.$
$ \Rightarrow \tan \widehat {ACB} = \tan (\widehat {OCB} - \alpha ) = \frac{{\tan \widehat {OCB} - \tan \alpha }}{{1 + \tan \widehat {OCB}.\tan \alpha }} = \frac{{\frac{{4\lambda }}{h}}}{{1 + \frac{{77{\lambda ^2}}}{{{h^2}}}}} = \frac{{4\lambda }}{{h + \frac{{77{\lambda ^2}}}{h}}}$
Áp dụng bất đẳng thức Cô si: $\tan \widehat{ACB}$ lớn nhất khi $h=\frac{77{{\lambda }^{2}}}{h}\Rightarrow h=\sqrt{77}.\lambda $
Gọi M là điểm trên AC dao động ngược pha với nguồn.
${{d}_{M}}=(2k+1)\frac{\lambda }{2}$
Kẻ OH$ \bot $AC. Sử dụng hệ thức lượng trong tam giác vuông OAC :
$\begin{array}{l}
\frac{1}{{O{H^2}}} = \frac{1}{{O{C^2}}} + \frac{1}{{O{A^2}}} = \frac{1}{{77{\lambda ^2}}} + \frac{1}{{{7^2}{\lambda ^2}}} = \frac{{18}}{{539{\lambda ^2}}}\\
\Rightarrow OH = \frac{{7\sqrt {22} }}{6}\lambda
\end{array}$
Xét M trên đoạn HC:
$\begin{array}{l}
OH \le OM \le OC\\
\Rightarrow \frac{{7\sqrt {22} }}{6}\lambda \le (2k + 1)\frac{\lambda }{2} \le \sqrt {77} \lambda \\
\Rightarrow 4,97 \le k \le 8,27\\
\Rightarrow k = 5,6,7,8
\end{array}$
Có 4 giá trị k, như vậy trên đoạn HC có 4 vị trí dao động ngược pha với nguồn.
Tương tự xét M trên đoạn HA ta cũng tìm được 2 vị trí
Tổng cộng có 6 vị trí có điểm dao động ngược pha với nguồn.
Chọn C
Câu hỏi 17 :
Một nguồn phát sóng cơ hình sin đặt tại O, truyền dọc theo sợi dây đàn hồi căng ngang rất dài OA với bước sóng 48cm. Tại thời điểm t1 và t2 hình dạng của một đoạn dây tương ứng như đường 1 và đường 2 của hình vẽ, trục Ox trùng với vị trí cân bằng của sợi dây, chiều dương trùng với chiều truyền sóng. Trong đó M là điểm cao nhất, uM, uN, uH lần lượt là li độ của các điểm M, N, H. Biết \(u_M^2 = u_N^2 + u_H^2\) và biên độ sóng không đổi. Khoảng cách từ P đến Q bằng:
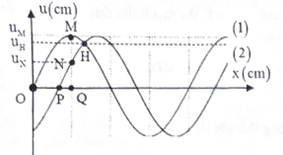
- A 12cm
- B 2cm
- C 6cm
- D 4cm
Đáp án: D
Phương pháp giải:
Phương pháp:
Sử dụng kĩ năng đọc đồ thị và đường tròn lượng giác
Công thức tính độ lệch pha giữa hai điểm trên phương truyền sóng: \(\Delta \varphi = \frac{{2\pi d}}{\lambda }\)
Lời giải chi tiết:
Cách giải:
Biểu diễn vị trí các điểm tại các thời điểm t1 và t2 trên đường tròn lượng giác ta có:
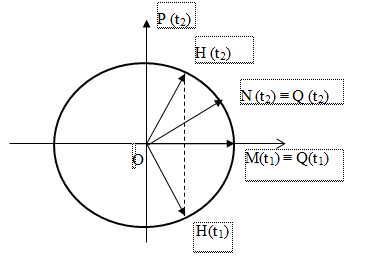
Theo bài ra ta có:
\(\begin{array}{l}u_M^2 = u_N^2 + u_H^2 \Leftrightarrow {A^2} = u_N^2 + u_H^2 \Leftrightarrow \frac{{u_N^2}}{{{A^2}}} + \frac{{u_H^2}}{{{A^2}}} = 1 \Rightarrow {u_N} \bot {u_H}\\ \Rightarrow \widehat {NOH} = \frac{\pi }{2}\,\,\,\left( 1 \right)\end{array}\)
Từ thời điểm t1 đến thời t2 H đi được góc 2α thì Q cũng đi được góc 2 (2)
Từ (1) và (2) \( \Rightarrow \widehat {NOM} = \frac{\pi }{3} \Rightarrow \widehat {PON} = \frac{\pi }{6} = \Delta {\varphi _{PQ}}\)
Mà: \(\Delta {\varphi _{PQ}} = \frac{{2\pi .PQ}}{\lambda } = \frac{\pi }{6} \Rightarrow PQ = \frac{\lambda }{{12}} = \frac{{48}}{{12}} = 4cm\)
Chọn D
Câu hỏi 18 :
Trên một sợi dây dài có sóng ngang, hình sin truyền qua. Hình dạng của một đoạn dây tại hai thời điểm t1 và t2 như hình vẽ bên. Li độ của các phần tử tại M và N ở thời điểm t1 lần lượt là 20,0mm và 15,3mm.Biết t2 - t1 = 0,05s và nhỏ hơn một chu kỳ sóng. Tốc độ cực đại của một phần tử trên dây gần đúng bằng
- A 0,32m/s.
- B 3,4m/s.
- C 3,2m/s.
- D 0,34m/s.
Đáp án: D
Phương pháp giải:
Áp dụng vòng tròn lượng giác trong sóng cơ học
Lời giải chi tiết:
Từ hình vẽ ta xác định được \(\left( {{t_1}} \right)\left\{ \begin{array}{l}{u_M} = 20mm \nearrow \\{u_N} = 15,3mm \nearrow \end{array} \right.;\left( {{t_2}} \right)\left\{ \begin{array}{l}{u_M} = 20mm \swarrow \\{u_N} = + A\end{array} \right.\) \(\)
Ta có \(\left\{ \begin{array}{l}\cos \frac{\alpha }{2} = \frac{{20}}{A}\\\cos \alpha = \frac{{15,3}}{A}\end{array} \right. = > 2{\cos ^2}\frac{\alpha }{2} - 1 = \frac{{15,3}}{A} \Leftrightarrow 2.{\left( {\frac{{20}}{A}} \right)^2} - 1 = \frac{{15,3}}{A} = > A = 21,6mm\)
Từ đó ta có \(\cos \alpha = \frac{{15,3}}{{21,6}} = > \alpha = \frac{\pi }{4}\), mà \(T \leftrightarrow 2\pi = > \frac{\pi }{4} \leftrightarrow \frac{T}{8} = 0,05s = > T = 0,4s\)
Tốc độ cực đại sóng truyền đi là \(v = \omega A = \frac{{2\pi }}{T}.A = \frac{{2\pi }}{{0,4}}.21,6 = 339mm/s \approx 0,34m/s\)
Chọn D
Câu hỏi 19 :
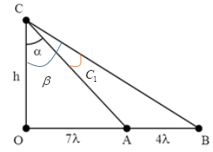
Một sóng cơ lan truyền trên sợi dây từ C đến B với chu kì T = 2 s, biên độ không đổi. Ở thời điểm t0, ly độ các phần tử tại B và C tương ứng là –20 mm và +20 mm, các phần tử tại trung điểm D của BC đang ở vị trí cân bằng. Ở thời điểm t1, li độ các phần tử tại B và C cùng là +8 mm. Tại thời điểm \({t_2} = {t_1} + 0,4\,\,s\) thì tốc độ dao động của phần tử D có giá trị gần nhất với giá trị nào sau đây
- A 67,67 mm/s
- B 64,36 mm/s
- C 58,61 mm/s
- D 33,84 mm/s
Đáp án: B
Phương pháp giải:
Sử dụng vòng tròn lượng giác và công thức: \(\Delta t = \dfrac{{\Delta \varphi }}{\omega }\)
Tần số góc của sóng: \(\omega = \dfrac{{2\pi }}{T}\)
Li độ tại hai thời điểm vuông pha: \({x_1}^2 + {x_2}^2 = {A^2}\)
Công thức độc lập với thời gian: \({v^2} = {\omega ^2}\left( {{A^2} - {u^2}} \right)\)
Lời giải chi tiết:
Tần số của sóng là: \(\omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{2} = \pi \,\,\left( {rad/s} \right)\)
Ta có vòng tròn lượng giác:
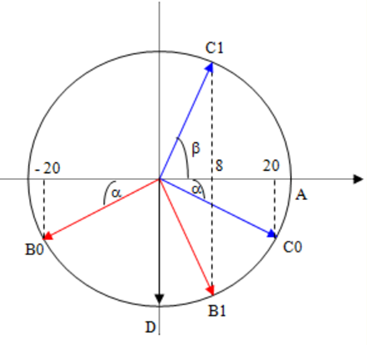
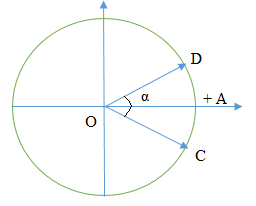
Từ vòng tròn lượng giác, ta thấy
\(\left\{ \begin{array}{l}\widehat {{C_0}O{C_1}} = \alpha + \beta \\\widehat {{B_0}O{B_1}} = \pi - \left( {\alpha + \beta } \right)\\\widehat {{C_0}O{C_1}} = \widehat {{B_0}O{B_1}}\end{array} \right. \Rightarrow \alpha + \beta = \pi - \left( {\alpha + \beta } \right) \Rightarrow \alpha + \beta = \dfrac{\pi }{2}\,\,\left( {rad} \right)\)
Hai thời điểm t0 và t1 vuông pha với nhau, ta có:
\({x_{0M}}^2 + {x_{1M}}^2 = {A^2} \Rightarrow A = \sqrt {{x_{0M}}^2 + {x_{1M}}^2} = \sqrt {{{20}^2} + {8^2}} = \sqrt {464} \,\,\left( {mm} \right)\)
Ở thời điểm t2, vecto của điểm D quay được góc: \(\Delta \varphi = \omega \Delta t = \pi .0,4 = 0,4\pi \,\,\left( {rad} \right)\)
Pha của điểm D ở thời điểm t2 là: \({\varphi _D} = \left( {\alpha + \beta + \Delta \varphi } \right) - \dfrac{\pi }{2} = \left( {\dfrac{\pi }{2} + 0,4\pi } \right) - \dfrac{\pi }{2} = 0,4\pi \,\,\left( {rad} \right)\)
Li độ của điểm D khi đó là: \({u_D} = A.cos{\varphi _D} = \sqrt {464} .cos\left( {0,4\pi } \right) = 6,66\,\,\left( {mm} \right)\)
Ta có công thức độc lập với thời gian:
\({v^2} = {\omega ^2}\left( {{A^2} - {u_D}^2} \right) = {\pi ^2}.\left[ {{{\left( {\sqrt {464} } \right)}^2} - 6,{{66}^2}} \right] \Rightarrow v = 64,36\,\,\left( {mm/s} \right)\)
Chọn B.
Câu hỏi 20 :
Một sóng hình sin truyền theo phương Ox từ nguồn O với tần số 20Hz, có tốc độ truyền sóng nằm trong khoảng từ 0,7m/s đến 1m/s. Gọi A và B là hai điểm nằm trên Ox, ở cùng một phía so với O và cách nhau 10cm. Hai phần tử môi trường tại A và B luôn dao động ngược pha với nhau. Tốc độ truyền sóng là:
- A 90cm/s
- B 100cm/s
- C 80cm/s
- D 85cm/s
Đáp án: C
Phương pháp giải:
Công thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi d.f}}{v}\)
Hai dao động ngược pha khi: \(\Delta \varphi = \left( {2k + 1} \right)\pi \)
Lời giải chi tiết:
Độ lệch pha của hai phần tử môi trường tại A và B là: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi d.f}}{v}\)
Hai phần tử này luôn dao động ngược pha nên:
\(\Delta \varphi = \dfrac{{2\pi d.f}}{v} = \left( {2k + 1} \right)\pi \Rightarrow v = \dfrac{{2d.f}}{{2k + 1}} = \dfrac{{2.0,1.20}}{{2k + 1}} = \dfrac{4}{{2k + 1}}\)
Do tốc độ truyền sóng nằm trong khoảng từ 0,7m/s đến 1m/s nên:
\(\begin{array}{l}0,7m/s < v < 1m/s \Leftrightarrow 0,7 < \dfrac{4}{{2k + 1}} < 1\\ \Leftrightarrow 1,5 < k < 2,36 \Rightarrow k = 2\\ \Rightarrow v = \dfrac{4}{{2k + 1}} = \dfrac{4}{{2.2 + 1}} = 0,8m/s = 80cm/s\end{array}\)
Chọn C.
Câu hỏi 21 :
Một sóng ngang hình sin truyền theo phương ngang dọc theo một sợi dây đàn hồi rất dài có biên độ không đổi và có bước sóng lớn hơn 30 cm. Trên dây có hai điểm A và B cách nhau 20 cm (A gần nguồn hơn so với B). Chọn trục Ox thẳng đứng chiều dương hướng lên, gốc tọa độ O tại vị trí cân bằng của nguồn. M và N tương ứng là hình chiếu của A và B lên trục Ox. Phương trình dao động của N có dạng \({x_N} = a\cos \left( {\omega t + \dfrac{\pi }{3}} \right)\,\,cm\), khi đó vận tốc tương đối của N đối với M biến thiên theo thời gian với phương trình \({v_{NM}} = b\cos \left( {20\pi t + \dfrac{{2\pi }}{3}} \right)\,\,cm/s\). Biết a, ω và b là các hằng số dương. Tốc độ truyền sóng trên dây là
- A 600 cm/s
- B 450 cm/s
- C 600 mm/s
- D 450 mm/s
Đáp án: A
Phương pháp giải:
Phương trình sóng tổng quát: \({u_M} = a\cos \left( {\omega t + \varphi - \dfrac{{2\pi d}}{\lambda }} \right)\)
Vận tốc dao động: v = x’
Tốc độ truyền sóng: \(v = \lambda f = \lambda \dfrac{\omega }{{2\pi }}\)
Lời giải chi tiết:
Do điểm A gần nguồn hơn so với B, nên dao động sớm pha hơn điểm B, phương trình dao động của điểm M là: \({x_M} = a\cos \left( {\omega t + \dfrac{\pi }{3} + \dfrac{{2\pi d}}{\lambda }} \right)\)
Vận tốc của hai điểm M và N lần lượt là:
\(\left\{ \begin{array}{l}{v_M} = {x_M}' = - a\omega \sin \left( {\omega t + \dfrac{\pi }{3} + \dfrac{{2\pi d}}{\lambda }} \right)\\{v_N} = {x_N}' = - a\omega \sin \left( {\omega t + \dfrac{\pi }{3}} \right)\end{array} \right.\)
Vận tốc tương đối của N đối với M là:
\(\begin{array}{l}{v_{NM}} = {v_N} - {v_M} = - a\omega \sin \left( {\omega t + \dfrac{\pi }{3}} \right) + a\omega \sin \left( {\omega t + \dfrac{{2\pi d}}{\lambda } + \dfrac{\pi }{3}} \right)\\ \Rightarrow {v_{NM}} = 2a\omega \sin \dfrac{{\pi d}}{\lambda }\cos \left( {\omega t + \dfrac{{\pi d}}{\lambda } + \dfrac{\pi }{3}} \right) = b\cos \left( {20\pi t + \dfrac{{2\pi }}{3}} \right)\\ \Rightarrow \left\{ \begin{array}{l}\omega = 20\pi \,\,\left( {rad/s} \right)\\\dfrac{{\pi d}}{\lambda } + \dfrac{\pi }{3} = \dfrac{{2\pi }}{3} + k2\pi \end{array} \right.\end{array}\)
Do \(\lambda > 30\,\,\left( {cm} \right) \Rightarrow \dfrac{{\pi .20}}{{30}} + \dfrac{\pi }{3} > \dfrac{{2\pi }}{3} + k2\pi \Rightarrow k < 0,17\)
\( \Rightarrow k = 0 \Rightarrow \dfrac{{\pi .20}}{\lambda } + \dfrac{\pi }{3} = \dfrac{{2\pi }}{3} \Rightarrow \lambda = 60\,\,\left( {cm} \right)\)
Tốc độ truyền sóng trên dây là: \(v = \lambda \dfrac{\omega }{{2\pi }} = 60.\dfrac{{20\pi }}{{2\pi }} = 600\,\,\left( {cm/s} \right)\)
Chọn A.
Câu hỏi 22 :
Một nguồn phát sóng cơ trên mặt nước đặt tại O, sóng có biên độ A, chu kì T, bước sóng λ. Hai điểm M, N cùng nằm trên một hướng truyền sóng cách nhau \(d = \frac{\lambda }{3}\), N gần nguồn hơn. Coi biên độ không đổi khi truyền đi. Tại thời điểm t1 = 0, M và N có li độ uM = + 3 cm và uN = - 3 cm. Ở thời điểm t2 liền sau đó, N có li độ uN = + A. Thời điểm t2 là:
- A \(\frac{{5T}}{6}\)
- B \(\frac{T}{{12}}\)
- C \(\frac{{11T}}{{12}}\)
- D \(\frac{{7T}}{{12}}\)
Đáp án: D
Phương pháp giải:
Sử dụng VTLG.
Hai điểm MN cách nhau \(d = \frac{\lambda }{3}\) tức là vecto OM cách vecto ON một góc \(\frac{{2\pi }}{3}\)
Vì M và N có li độ đối xứng nhau nên ta biểu diễn được trên VTLG.
Lời giải chi tiết:
Hai điểm MN cách nhau \(d = \frac{\lambda }{3}\) tức là vecto OM cách vecto ON một góc \(\frac{{2\pi }}{3}\)
Vì M và N có li độ đối xứng nhau nên ta có hình vẽ:
Vậy N đến vị trí có li độ A lần đầu tiên thì ON quét được một góc là:
\(\alpha = \frac{\pi }{6} + \pi = \frac{{7\pi }}{6}\)
Vậy thời gian để N có li độ A là:
\(t = \frac{\alpha }{{2\pi }}.T = \frac{7}{{12}}.T\)
Chọn D.
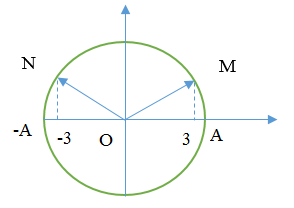
Câu hỏi 23 :
Cho sóng ngang truyền trên sợi dây dài có bước sóng \(60cm\), biên độ \(8\sqrt 5 cm\) không đổi. Ba phần tử M, N, P trên dây có vị trí cân bằng cách vị trí cân bằng của nguồn lần lượt là 10cm, 40cm, 55cm. Tại thời điểm khi sóng đã truyền qua cả ba phần tử và vị trí tức thời của M, N, P thẳng hàng thì khoảng cách NP là
- A 24cm.
- B 17cm.
- C 15cm.
- D 20cm.
Đáp án: B
Phương pháp giải:
+ Sử dụng biểu thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
+ Sử dụng công thức tính khoảng cách: \(NP = \sqrt {\Delta {x^2} + \Delta {u^2}} \)
Lời giải chi tiết:
Ta có:
\(\left\{ \begin{array}{l}\Delta {\varphi _{MN}} = \dfrac{{2\pi .30}}{{60}} = \pi \\\Delta {\varphi _{NP}} = 2\pi \dfrac{{15}}{{60}} = \dfrac{\pi }{2}\end{array} \right.\)
\( \Rightarrow \) M và N ngược pha nhau \( \Rightarrow {u_N} = - {u_M}\)
N và P vuông pha nhau
\( \Rightarrow {\left( {\dfrac{{{u_N}}}{A}} \right)^2} + {\left( {\dfrac{{{u_P}}}{A}} \right)^2} = 1\)
\( \Rightarrow u_N^2 + u_P^2 = {A^2} = {\left( {8\sqrt 5 } \right)^2}\) (1)
Từ đồ thị ta có \({u_N} = \dfrac{1}{2}{u_P}\) (2)
Từ (1) và (2) ta suy ra: \(\left\{ \begin{array}{l}{u_N} = 8cm\\{u_P} = 16cm\end{array} \right.\)
Khoảng cách \(NP = \sqrt {\Delta {x^2} + \Delta {u^2}} \)
Có \(\left\{ \begin{array}{l}\Delta x = 15cm\\\Delta u = {u_P} - {u_N} = 16 - 8 = 8cm\end{array} \right.\)
\( \Rightarrow NP = \sqrt {{{15}^2} + {8^2}} = 17cm\)
Chọn B
Câu hỏi 24 :
Một sóng ngang hình sin truyền theo phương ngang dọc theo một sợi dây đàn hồi rất dài có biên độ không đổi và có bước sóng lớn hơn 30cm. Trên dây có hai điểm A và B cách nhau 20cm (A gần nguồn hơn so với B). Chọn trục Ox thẳng đứng chiều dương hướng lên, gốc tọa độ O tại vị trí cân bằng của nguồn. M và N tương ứng là hình chiếu của A và B lên trục Ox. Phương trình dao động của N có dạng \({x_N} = acos\left( {\omega t + \dfrac{\pi }{3}} \right)\) khi đó vận tốc tương đối của N đối với M biến thiên theo thời gian với phương trình \({v_{NM}} = bcos\left( {20\pi t + \dfrac{{2\pi }}{3}} \right)\). Biết \(a,\omega \) và \(b\) là các hằng số dương. Tốc độ truyền sóng trên dây là
- A
\(450mm/s\)
- B \(450cm/s\)
- C \(600cm/s\)
- D \(600mm/s\)
Đáp án: C
Phương pháp giải:
+ Sử dụng công thức lượng giác
+ Sử dụng biểu thức tính vận tốc: \(v = x'\)
+ Vận dụng tính tương đối của vận tốc
+ Sử dụng biểu thức: \(v = \lambda f\)
Lời giải chi tiết:
Ta có, phương trình sóng tại A và B chính là phương trình dao động của M và N. A nhanh pha hơn B suy ra M nhanh pha hơn N
Phương trình sóng tại M: \({x_M} = acos\left( {\omega t + \dfrac{\pi }{3} + \dfrac{{2\pi d}}{\lambda }} \right)\)
\( \Rightarrow \left\{ \begin{array}{l}{v_M} = - a\omega \sin \left( {\omega t + \dfrac{\pi }{3} + \dfrac{{2\pi d}}{\lambda }} \right)\\{v_N} = - a\omega \sin \left( {\omega t + \dfrac{\pi }{3}} \right)\end{array} \right.\)
\({v_{NM}} = {v_N} - {v_M} = a\omega \sin \dfrac{{\pi d}}{\lambda }\left[ {2cos\left( {\omega t + \dfrac{\pi }{3} + \dfrac{{\pi d}}{\lambda }} \right)} \right] = bcos\left( {20\pi t + \dfrac{{2\pi }}{3}} \right)\)
Đồng nhất phương trình, ta suy ra: \(\left\{ \begin{array}{l}2a\omega \sin \dfrac{{\pi d}}{\lambda } = b\\\omega = 20\pi \\\dfrac{\pi }{3} + \dfrac{{\pi d}}{\lambda } = \dfrac{{2\pi }}{3}\end{array} \right.\)
\( \Rightarrow \dfrac{{\pi d}}{\lambda } = \dfrac{\pi }{3} \Rightarrow \lambda = 3d = 3.20 = 60cm\)
\( \Rightarrow v = \lambda .f = \lambda .\dfrac{\omega }{{2\pi }} = 60.\dfrac{{20\pi }}{{2\pi }} = 600cm/s\)
Chọn C
Câu hỏi 25 :
Tại thời điểm đầu tiên t = 0 đầu O của sợi dây cao su căng thẳng nằm ngang bắt đầu dao động đi lên với tần số 2 Hz với biên độ \(A = 6\sqrt 5 cm\). Gọi P, Q là hai điểm cùng nằm trên một phương truyền sóng cách O lần lượt là 6 cm và 9 cm. Biết vận tốc truyền sóng trên dây là 24 cm/s và coi biên độ sóng không đối khi truyền đi. Tại thời điểm O, P, Q thẳng hàng lần thứ 2 thì vận tốc dao động của điểm P và điểm Q lần lượt là vP và vQ. Chọn phương án đúng
- A vQ = 24π cm/s.
- B vP = 48π cm/s.
- C vQ = −24π cm/s.
- D vP = −24π cm/s.
Đáp án: B
Phương pháp giải:
Bước sóng: \(\lambda = \frac{v}{f}\)
Công thức tính độ lệch pha: \(\Delta \varphi = \frac{{2\pi d}}{\lambda }\)
Phương trình sóng: \(u = A.cos\left( {\omega t + \varphi } \right)\)
Phương trình vận tốc của phần tử sóng: v= u'
Lời giải chi tiết:
Bước sóng: \(\lambda = \frac{v}{f} = \frac{{24}}{2} = 12cm\)
Sử dụng công thức tính độ lệch pha:
\(\Delta \varphi = \frac{{2\pi d}}{\lambda }\), ta có:
+ P cách O nửa bước sóng do vậy P luôn ngược pha với O
+ Q cách O một khoảng 0,75λ nên Q luôn vuông pha với O.
+ Q cách P một phần tư bước sóng, do đó Q cũng vuông pha với P.
Ta có hình vẽ:
Từ hình vẽ, ta thấy rằng khi O,P,Q thẳng hàng thì:
\(\frac{{{u_Q}}}{{{u_P}}} = \frac{6}{3} = 2 \Rightarrow {u_Q} = 2{u_P}\)
Mặt khác P và Q luôn cùng pha nên ta có:
\(\left\{ \begin{array}{l}
\left| {{v_P}} \right| = \omega A\sqrt {1 - {{\left( {\frac{{{u_P}}}{A}} \right)}^2}} = 48{\pi _{}}cm/s\\
\left| {{v_Q}} \right| = \omega A\sqrt {1 - {{\left( {\frac{{{u_Q}}}{A}} \right)}^2}} = 24{\pi _{}}cm/s
\end{array} \right.\)
Tốc độ của điểm P và Q tương ứng là
\(\left\{ \begin{array}{l}
\left| {{v_P}} \right| = \omega A\sqrt {1 - {{\left( {\frac{{{u_P}}}{A}} \right)}^2}} = 48{\pi _{}}cm/s\\
\left| {{v_Q}} \right| = \omega A\sqrt {1 - {{\left( {\frac{{{u_Q}}}{A}} \right)}^2}} = 24{\pi _{}}cm/s
\end{array} \right.\)
Lần thẳng hàng thứ 2 ứng với \({v_Q} = 24\pi cm/s\)
Chọn B.
Câu hỏi 26 :
Một sóng hình sin lan truyền trên mặt nước từ nguồn O với bước sóng \(\lambda \). Ba điểm A, B, C trên hai phương truyền sóng sao cho OA vuông góc với OC và B là một điểm thuộc tia OA sao cho OB > OA. Biết \(OA = 7\lambda \). Tại thời điểm người ta qua sát thấy giữa A và B có 5 đỉnh sóng (kể cả A và B) và lúc này góc ACB đạt giá trị lớn nhất. Số điểm dao động ngược pha với nguồn trên đoạn AC bằng
- A 4
- B 5
- C 6
- D 7
Đáp án: C
Phương pháp giải:
+ Sử dụng công thức lượng giác
+ Sử dụng biểu thức: \(\tan \left( {a - b} \right) = \dfrac{{{\rm{tana - tanb}}}}{{1 + \tan a.\tan b}}\)
+ Sử dụng biểu thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
+ Điều kiện ngược pha: \(\Delta \varphi = \left( {2k + 1} \right)\pi \)
Lời giải chi tiết:
Ta có, giữa A và B có 5 đỉnh sóng với A, B cũng là đỉnh sóng
\( \Rightarrow AB = 4\lambda \)
Ta có: \(\left\{ \begin{array}{l}\tan \alpha = \dfrac{{7\lambda }}{h}\\\tan \beta = \dfrac{{7\lambda + 4\lambda }}{h} = \dfrac{{11\lambda }}{h}\end{array} \right.\)
Ta có: \(\beta - \alpha = {C_1}\)
\( \Rightarrow \tan \left( {\beta - \alpha } \right) = \dfrac{{\tan \beta - \tan \alpha }}{{1 + \tan \beta \tan \alpha }} = \dfrac{{\dfrac{{11\lambda }}{h} - \dfrac{{7\lambda }}{h}}}{{1 + \dfrac{{11\lambda }}{h}.\dfrac{{7\lambda }}{h}}} = \dfrac{{4\lambda }}{{h + \dfrac{{77{\lambda ^2}}}{h}}}\)
Từ biểu thức trên, ta thấy \({C_1} = \widehat {ACB}\) lớn nhất khi mẫu nhỏ nhất
Có \(h + \dfrac{{77{\lambda ^2}}}{h} \ge 2\sqrt {77{\lambda ^2}} \)
Dấu “=” xảy ra khi \(h = \sqrt {77} \lambda \)
+ Gọi M là một điểm trên AC, để M dao động ngược pha với nguồn thì \(\Delta {\varphi _M} = \dfrac{{2\pi {d_M}}}{\lambda } = \left( {2k + 1} \right)\pi \)
\( \Rightarrow {d_M} = \left( {2k + 1} \right)\dfrac{\lambda }{2}\)
+ Xét khoảng giá trị của M, tính về phía C từ đường vuông góc của O lên AC, ta có:
\(5,47\lambda \le {d_M} \le 8,7\lambda \)
Sử dụng chức năng TABLE trong máy tính ta tìm được 4 vị trí
+ Xét đoạn về phía A: \(5,47\lambda \le {d_M} \le 7\lambda \)
Cũng sử dụng chức năng TABLE trong máy tính ta tìm được 2 vị trí
Vậy trên AC có 6 vị trí
Chọn C
Câu hỏi 27 :
Xét một sóng ngang có tần số \(f{\rm{ }} = {\rm{ }}10{\rm{ }}Hz\) và biên độ \(a = 2\sqrt 2 cm\), lan truyền theo phương Ox từ nguồn dao động O, với tốc độ truyền sóng là\(40{\rm{ }}cm/s\). Điểm P nằm trên phương truyền sóng, có tọa độ \(x = 17cm\). Khoảng cách lớn nhất giữa phần tử môi trường tại O và phần tử môi trường tại P là
- A 22 cm.
- B 17,46 cm
- C 22,66 cm.
- D 21 cm.
Đáp án: B
Phương pháp giải:
+ Sử dụng biểu thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
+ Viết phương trình sóng tại các điểm
+ Sử dụng máy tính tổng hợp dao động
+ Sử dụng công thức tính khoảng cách
Lời giải chi tiết:
Ta có:
+ Tần số góc: \(\omega = 2\pi f = 20\pi \left( {rad/s} \right)\)
+ Bước sóng: \(\lambda = \dfrac{v}{f} = 4cm\)
Giả sử phương trình sóng tại O: \({u_O} = 2\sqrt 2 cos\left( {20\pi t} \right)\)
\( \Rightarrow \) Phương trình sóng tại P: \({u_P} = 2\sqrt 2 cos\left( {20\pi t - \dfrac{{2\pi .17}}{4}} \right) = 2\sqrt 2 cos\left( {20\pi t - \dfrac{\pi }{2}} \right)\)
Khoảng cách OP: \(OP = \sqrt {{x^2} + {{\left( {{u_O} - {u_P}} \right)}^2}} \)
\(O{P_{max}}\) khi \({\left[ {{u_O} - {u_P}} \right]_{max}}\)
Ta có: \({u_O} - {u_P} = 2\sqrt 2 \angle 0 - 2\sqrt 2 \angle - \dfrac{\pi }{2} = 4\angle - \dfrac{\pi }{4}\)
\( \Rightarrow {\left[ {{u_O} - {u_P}} \right]_{max}} = 4cm\)
Khi đó ta có: \(O{P_{max}} = \sqrt {{{17}^2} + {4^2}} = 17,46cm\)
Chọn B
Câu hỏi 28 :
Một sóng hình sin lan truyền trên phương Ox với tân số 10 Hz. Tại thời điểm t1 hai phần tử M và N gần nhau nhất có cùng li độ tương ứng là -1,6cm và 1,6cm. Tại thời điểm t2 gần t1nhất thì li độ của M và N đều bằng nhau và bằng 1,2cm. Tốc độ cực đại của các phần tử trên phương truyền sóng gần nhất với giá trị nào sau đây ?
- A 130 cm/s.
- B 100 cm/s.
- C 116 cm/s.
- D 124 cm/s.
Đáp án: D
Phương pháp giải:
Sử dụng VTLG và tìm được biên độ A.
Tốc độ cực đại: \({v_{\max }} = \omega A = 2\pi fA\)
Lời giải chi tiết:
Ban đầu M và N có li độ -1,6 cm và 1,6 cm, ta có ĐTLG
Vì M và N là là hai phần tử gần nhau nhất, nên từ hình vẽ, ta lấy đó là điểm M1 và N1
Khi M và N có li độ 1,2 cm, ta có ĐTLG
Vậy từ t1 đến t2góc quét của hai vecto \(\overrightarrow {OM} \) và \(\overrightarrow {ON} \) như nhau.
Ta có:
\(\arcsin \frac{{1,6}}{A} + \arcsin \frac{{1,2}}{A} = {\rm{arccos}}\frac{{1,6}}{A} + \arccos \frac{{1,2}}{A}\)
Bấm máy tính và tìm được A = 2cm
Tốc độ cực đại của các phần tử là:
\(v = \omega A = 2\pi fA = 40\pi \approx 124\left( {cm/s} \right)\)
Chọn D.
Câu hỏi 29 :
Một sóng ngang hình sin truyền theo phương ngang dọc theo một sợi dây đàn hồi rất dài có biên độ không đổi và có bước sóng lớn hơn 30cm. Trên dây có hai điểm A và B cách nhau 20cm (A gần nguồn hơn so với B). Chọn trục Ox thẳng đứng chiều dương hướng lên, gốc tọa độ O tại vị trí cân bằng của nguồn. M và N tương ứng là hình chiếu của A và B lên trục Ox. Phương trình dao động của N có dạng \({x_N} = acos\left( {\omega t + \dfrac{\pi }{3}} \right)\) khi đó vận tốc tương đối của N đối với M biến thiên theo thời gian với phương trình \({v_{NM}} = bcos\left( {20\pi t + \dfrac{{2\pi }}{3}} \right)\). Biết \(a,\omega \) và \(b\) là các hằng số dương. Tốc độ truyền sóng trên dây là
- A \(450mm/s\)
- B \(450cm/s\)
- C \(600mm/s\)
- D \(600cm/s\)
Đáp án: D
Phương pháp giải:
Vận tốc tương đối: \({v_{NM}} = {v_N} - {v_M}\)
Công thức lượng giác: \(\sin x - \sin y = 2\cos \dfrac{{x + y}}{2}\sin \dfrac{{x - y}}{2}\)
Vận tốc truyền sóng: \(v = \lambda f\)
Lời giải chi tiết:
Điểm A gần nguồn hơn so với B → A sớm pha hơn B → M sớm pha hơn N
Theo đề bài ta có: \({x_N} = a\cos \left( {\omega t + \dfrac{\pi }{3}} \right) \Rightarrow {x_M} = a\cos \left( {\omega t + \dfrac{\pi }{3} + \dfrac{{2\pi d}}{\lambda }} \right)\)
Mặt khác, vận tốc tương đối của N đối với M là:
\({v_{NM}} = {v_N} - {v_M} = b\cos \left( {20\pi t + \dfrac{{2\pi }}{3}} \right)\)
Ta có: \({v_N} = {x_N}' = - \omega a\sin \left( {\omega t + \dfrac{\pi }{3}} \right)\)
\({v_M} = {x_M}' = - \omega a\sin \left( {\omega t + \dfrac{\pi }{3} + \dfrac{{2\pi d}}{\lambda }} \right)\)
\(\begin{array}{l} \Rightarrow {v_N} - {v_M} = - \omega a\left[ {\sin \left( {\omega t + \dfrac{\pi }{3}} \right) - \sin \left( {\omega t + \dfrac{\pi }{3} + \dfrac{{2\pi d}}{\lambda }} \right)} \right]\\ \Rightarrow {v_N} - {v_M} = - 2\omega a\left[ {\cos \left( {\omega t + \dfrac{\pi }{3} + \dfrac{{\pi d}}{\lambda }} \right)\sin \left( { - \dfrac{{\pi d}}{\lambda }} \right)} \right]\\ \Rightarrow {v_N} - {v_M} = 2\omega a\sin \dfrac{{\pi d}}{\lambda }\cos \left( {\omega t + \dfrac{\pi }{3} + \dfrac{{\pi d}}{\lambda }} \right)\end{array}\)
Đồng nhất hai phương trình, ta có:
\(\begin{array}{l}\omega = 20\pi \,\,\left( {rad/s} \right) \Rightarrow f = \dfrac{\omega }{{2\pi }} = \dfrac{{20\pi }}{{2\pi }} = 10\,\,\left( {Hz} \right)\\\dfrac{\pi }{3} + \dfrac{{\pi d}}{\lambda } = \dfrac{{2\pi }}{3} \Rightarrow \dfrac{{\pi d}}{\lambda } = \dfrac{\pi }{3} \Rightarrow \lambda = 3d = 3.20 = 60\,\,\left( {cm} \right)\\ \Rightarrow v = \lambda f = 60.10 = 600\,\,\left( {cm/s} \right)\end{array}\)
Chọn D.
Câu hỏi 30 :
Một sóng cơ truyền trên sợi dây dài, nằm ngang, dọc theo chiều dương của trục Ox với tốc độ truyền sóng là v và biên độ không đổi. Tại thời điểm to = 0, phần tử tại O bắt đầu dao động từ vị trí cân bằng theo chiều âm của trục Ou. Tại thời điểm t1 = 0,3 s hình ảnh của một đoạn dây như hình vẽ. Khi đó vận tốc dao động của phần tử tại D là \({v_D} = \frac{{\rm{\pi }}}{{\rm{8}}}{\rm{v}}\) và quãng đường phần tử E đã đi được là 24 cm. Biết khoảng cách cực đại giữa hai phần tử là 5cm. Phương trình truyền sóng là
- A \(u = \cos \left( {\frac{{40\pi }}{3}t - \frac{{\pi x}}{3} - \frac{\pi }{2}} \right)cm\,\) (x tính bằng cm; t tính bằng s).
- B \(u = \cos \left( {20\pi t - \frac{{\pi x}}{3} + \frac{\pi }{2}} \right)\,cm\,\) (x tính bằng cm; t tính bằng s).
- C \(u = 3\cos \left( {20\pi t - \frac{{\pi x}}{{12}} + \frac{\pi }{2}} \right)\,cm\,\) (x tính bằng cm; t tính bằng s).
- D \(u = 3\cos \left( {\frac{{40\pi }}{3}t - \frac{{\pi x}}{{12}} - \frac{\pi }{2}} \right)\,cm\,\) (x tính bằng cm; t tính bằng s).
Đáp án: C
Phương pháp giải:
Thời điểm đầu tiên sóng bắt đầu từ O nên:
\({u_O} = A.\cos {\left( {\omega t + \frac{\pi }{2}} \right)_{}}cm\)
Sau thời gian t = 0,3s, sóng có dạng như hình vẽ, điểm O lại đang ở VTCB và chuyển động về biên âm nên: \(t = 0,3s = nT\)
Dễ thấy từ O đến E là một bước sóng ứng với 6 ô li, nên sóng truyền từ O đến E mất thời gian 1 chu kì T. Vì vậy quãng đường mà E đi được trong thời gian trên là: \(S = \left( {n - 1} \right).4A\)
Hai điểm C và D đều đang cách đỉnh sóng một khoảng nửa ô li nên biên độ của D là \({x_D} = \frac{{\sqrt 3 }}{2}A\) và vận tốc của D lúc đó là \({v_D} = \frac{1}{2}{v_{\max }} = \frac{1}{2}.\omega A\)
Vận tốc sóng \(v = \lambda .f\)
Khoảng cách giữa vtcb của C và D ứng với 1 ô li, khoảng cách giữa hai điểm C và D là \(CD = \sqrt {{d^2} + {{({u_C} - {u_D})}^2}} \)
Lời giải chi tiết:
Thời điểm đầu tiên sóng bắt đầu từ O nên: \({u_O} = A.\cos {\left( {\omega t + \frac{\pi }{2}} \right)_{}}cm\)

Sau thời gian t = 0,3s, sóng có dạng như hình vẽ, điểm O lại đang ở vtcb và chuyển động về biên âm nên:
\(t = 0,3s = nT\)
Dễ thấy từ O đến E là một bước sóng ứng với 6 ô li, nên sóng truyền từ O đến E mất thời gian 1 chu kì T. Vì vậy quãng đường mà E đi được trong thời gian trên là: \(S = \left( {n - 1} \right).4A\)
Hai điểm C và D đều đang cách đỉnh sóng một khoảng nửa ô li nên biên độ của D là và vận tốc của D lúc đó là:
\(\begin{array}{l}
{v_D} = \frac{1}{2}{v_{\max }} = \frac{1}{2}.\omega A\\
\Rightarrow \frac{1}{2}\omega A = \frac{\pi }{8}v = \frac{\pi }{8}.\lambda .f = \frac{\pi }{8}.\lambda .\frac{\omega }{{2\pi }} \Rightarrow \lambda = 8A
\end{array}\)
Ta có VTLG:
Khoảng cách giữa VTCB của C và D ứng với 1 ô li tức là \(CD = \frac{\lambda }{6}\) và \(\alpha = \frac{\pi }{3}\) ,
Khoảng cách giữa hai điểm C và D là:
\(CD = \sqrt {{d^2} + {{({u_C} - {u_D})}^2}} \)
Khoảng cách giữa hai điểm C và D cực đại là 5 cm khi (uC – uD) cực đại.
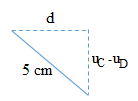
Ta có
\({u_C} - {u_D} = A.\cos \left( {\omega t - \frac{\pi }{3}} \right) \Rightarrow {\left( {{u_C} - {u_D}} \right)_{\max }} = A\)
\(\begin{array}{l}
CD = \sqrt {{d^2} + {{({u_C} - {u_D})}^2}} \Rightarrow 5 = \sqrt {{{\left( {\frac{\lambda }{6}} \right)}^2} + {{({u_C} - {u_D})}^2}} = \sqrt {{{\left( {\frac{{8A}}{6}} \right)}^2} + {A^2}} \\
\Rightarrow A = 3cm \Rightarrow \lambda = 8A = 24cm
\end{array}\)
Ta có: \(S = (n - 1).4A = 24 \Rightarrow n = 3\)
Lại có: \(t = 0,3s = 3T \Rightarrow T = 0,1s \Rightarrow \omega = \frac{{2\pi }}{T} = 20\pi \left( {rad/s} \right)\)
Vậy ta có phương trình truyền sóng là:
\(u = 3.\cos \left( {20\pi t + \frac{\pi }{2} - \frac{{2\pi x}}{{24}}} \right) = 3.\cos \left( {20\pi t + \frac{\pi }{2} - \frac{{\pi x}}{{12}}} \right)cm\)
Chọn C.
Câu hỏi 31 :
Ở mặt nước, một nguồn sóng đặt tại điểm O dao động điều hòa theo phương thẳng đứng. Sóng truyền trên mặt nước có bước sóng 5 cm, M và N là hai điểm trên mặt nước mà phần tử nước ở đó dao động cùng pha với nguồn. Trên các đoạn OM, ON và MN có số điểm mà phần tử nước ở đó dao động ngược pha với nguồn lần lượt là 5, 3 và 3. Độ dài đoạn MN có giá trị gần nhất với giá trị nào sau đây ?
- A 25 cm.
- B 20 cm.
- C 31 cm.
- D 10 cm.
Đáp án: C
Phương pháp giải:
Khi sóng truyền trên mặt nước, hai điểm dao động cùng pha khi khoảng cách giữa chúng là \(d = k\lambda \)
Hai điểm dao động ngược pha khi khoảng cách giữa chúng là\(d = \left( {k + 0,5} \right)\lambda \)
Áp dụng hệ thức lượng trong tam giác.
Lời giải chi tiết:
Vi M dao động cùng pha với nguồn, giữa M với O có 5 điểm ngược pha nên:
\(OM = 5\lambda = 25cm\)
Vì N dao động cùng pha với nguồn, giữa N và O có 3 điểm ngược pha nên:
\(ON = 3\lambda = 15cm\)
Các đường nét liền thể hiện cho các điểm dao động cùng pha và các đường nét đứt thể hiện cho các đường dao động ngược pha.
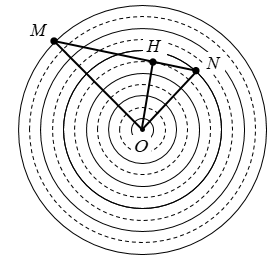
Để trên MN có 3 điểm dao động ngược pha, thì H là chân đường cao kẻ từ O xuống MN và là điểm dao động ngược pha với nguồn nên:
\(OH = 2,5\lambda = 12,{5_{}}cm\)
Vậy độ dài đoạn MN là:
\(\begin{array}{l}
MN = \sqrt {O{M^2} - O{H^2}} + \sqrt {O{N^2} - O{H^2}} \\
\,\,\,\,\,\,\,\,\,\, = \sqrt {{{25}^2} - 12,{5^2}} + \sqrt {{{15}^2} - 12,{5^2}} = 29,9cm
\end{array}\)
→ Gần nhất với giá trị 31 cm.
Chọn C.
Câu hỏi 32 :
Một sóng cơ truyền trên sợi dây dài, nằm ngang, dọc theo chiều dương của trục Ox với tốc độ truyền sóng là v và biên độ không đổi. Tại thời điểm to = 0, phần tử tại O bắt đầu dao động từ vị trí cân bằng theo chiều âm của trục Ou. Tại thời điểm t1 = 0,3 s hình ảnh của một đoạn dây như hình vẽ. Khi đó vận tốc dao động của phần tử tại \(D\)là vD = \(\dfrac{{\rm{\pi }}}{{\rm{8}}}{\rm{v}}\) và quãng đường phần tử E đã đi được là 24 cm. Biết khoảng cách cực đại giữa hai phần tử \(C,D\)là 5cm. Phương trình truyền sóng là
- A \(u = \cos (\dfrac{{40\pi }}{3}t - \dfrac{{\pi x}}{3} - \dfrac{\pi }{2})\,cm\,\)(x tính bằng cm; t tính bằng s).
- B \(u = \cos (20\pi t - \dfrac{{\pi x}}{3} + \dfrac{\pi }{2})\,cm\,\)(x tính bằng cm; t tính bằng s).
- C \(u = 3\cos (20\pi t - \dfrac{{\pi x}}{{12}} + \dfrac{\pi }{2})\,cm\,\)(x tính bằng cm; t tính bằng s).
- D \(u = 3\cos (\dfrac{{40\pi }}{3}t - \dfrac{{\pi x}}{{12}} - \dfrac{\pi }{2})\,cm\,\)(x tính bằng cm; t tính bằng s).
Đáp án: C
Phương pháp giải:
Phương trình sóng tổng quát: \(u = a\cos \left( {\omega t + \varphi - \dfrac{{2\pi x}}{\lambda }} \right)\)
Lời giải chi tiết:
Tại thời điểm \({t_0} = 0\), phần tử tại O bắt đầu dao động từ VTCB theo chiều âm của trục Ou
→ pha ban đầu của phần tử O là: \(\varphi = \dfrac{\pi }{2}\,\,\left( {rad} \right)\)
Nhận xét: trạng thái của O ở hai thời điểm \({t_0} = 0\) và \({t_1} = 0,3\,\,s\) giống nhau
\( \Rightarrow \Delta t = {t_1} - {t_0} = 0,3\,\,\left( s \right) = mT\)
Gọi độ dài của 1 ô là a → OE = λ = 6 ô \( \Rightarrow OE = \lambda = 6a \Rightarrow \lambda = 6a \Rightarrow a = \dfrac{\lambda }{6}\)
Độ lệch pha giữa hai điểm C và D là: \(\Delta {\varphi _{C/D}} = \dfrac{{2\pi .CD}}{\lambda } = \dfrac{{2\pi .\lambda }}{{6\lambda }} = \dfrac{\pi }{3}\,\,\left( {rad} \right)\)
Vận tốc của điểm D là: \({v_D} = \dfrac{\pi }{8}v = \dfrac{\pi }{8}.\left( {\lambda f} \right) = \dfrac{\pi }{8}.\lambda .\dfrac{\omega }{{2\pi }} = \dfrac{{\lambda \omega }}{{16}}\)
Nhận xét: D cách đỉnh sóng đoạn bằng \(\dfrac{a}{2} \Leftrightarrow \dfrac{a}{{12}}\) (ứng với góc \(\dfrac{\pi }{6}\))
\(\begin{array}{l} \Rightarrow {x_D} = \dfrac{{A\sqrt 3 }}{2} \Rightarrow {v_D} = \dfrac{{A\omega }}{2}\\ \Rightarrow \dfrac{{\lambda \omega }}{{16}} = \dfrac{{A\omega }}{2} \Rightarrow 16A = 2\lambda \Rightarrow A = \dfrac{{2\lambda }}{{16}} = \dfrac{\lambda }{8}\end{array}\)
Khoảng cách giữa hai điểm C và D là: \(\Delta = \sqrt {{d^2} + {{\left( {\Delta u} \right)}^2}} \,\,\left( * \right)\)
Để \({\Delta _{\max }} \Rightarrow {\left( {\Delta u} \right)_{\max }}\)
Ta có \({\left( {\Delta u} \right)_{\max }} = 2a\sin \dfrac{{\Delta \varphi }}{2} = a\)
Thay vào (*) ta có: \({5^2} = {\left( {\dfrac{\lambda }{6}} \right)^2} + {a^2} = {\left( {\dfrac{\lambda }{6}} \right)^2} + {\left( {\dfrac{\lambda }{8}} \right)^2} \Rightarrow \lambda = 24\,\,\left( {cm} \right)\)
Biên độ \(A = \dfrac{\lambda }{8} = \dfrac{{24}}{8} = 3\,\,\left( {cm} \right)\)
Thời gian sóng truyền từ O tới E là T
\(\begin{array}{l} \Rightarrow {S_E} = \left( {m - 1} \right).4A \Rightarrow 24 = \left( {m - 1} \right).4.3 \Rightarrow m = 3\\ \Rightarrow 0,3\,\,\left( s \right) = 3T \Rightarrow T = 0,1\,\,\left( s \right) \Rightarrow \omega = \dfrac{{2\pi }}{T} = 20\pi \,\,\left( {rad/s} \right)\end{array}\)
Phương trình sóng là: \(u = A\cos \left( {20\pi t + \dfrac{\pi }{2} - \dfrac{{2\pi x}}{{24}}} \right) = 3\cos \left( {20\pi t + \dfrac{\pi }{2} - \dfrac{{\pi x}}{{12}}} \right)\)
Chọn C.