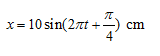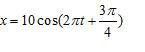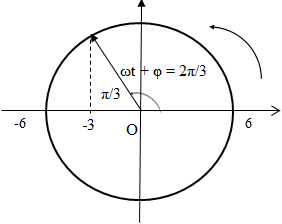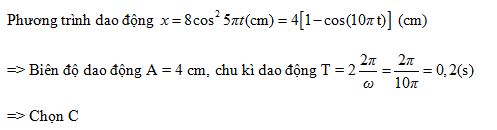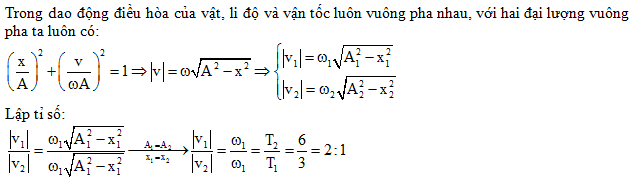Câu hỏi 1 :
Một vật dao động điều hòa với biên độ A=12cm và chu kì T=0,4s. Tốc độ trung bình lớn nhất của vật trong khoảng thời gian 1/15s là
- A 1,8m/s.
- B 1,2m/s.
- C 1,5m/s.
- D 2,1m/s.
Đáp án: A
Lời giải chi tiết:
Đáp án A
Phương pháp : Áp dụng công thức tính tốc độ trung bình
\(\Delta t = {1 \over {15}} = {T \over 6}\)
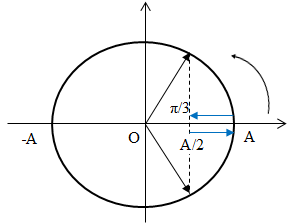
Để tốc độ trung bình lớn nhất thì quãng đường đi được lớn nhất và bằng A = 12cm.
\({v_{tb}} = {{12} \over {1/15}} = 180cm/s\)
Câu hỏi 2 :
Vật dao động điều hòa với phương trình x = 5cos(4 πt + π/6) cm. Tìm quãng đường lớn nhất vật đi được trong khoảng thời gian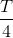 
:
- A 5cm
- B $$5\sqrt 2 $$
- C $$5\sqrt 3 $$
- D 10cm
Đáp án: B
Phương pháp giải:
Áp dụng công thức tính quãng đường lớn nhất.
$${S_{{\rm{max}}}} = 2{\rm{Asin}}{{\omega \Delta t} \over 2}$$
Lời giải chi tiết:
Quãng đường lớn nhất vật đi được trong khoảng thời gian $${T \over 4}$$ là:
$${S_{{\rm{max}}}} = 2{\rm{Asin}}{{\omega \Delta t} \over 2} = 2{\rm{Asin}}{{\omega {T \over 4}} \over 2} = 2{\rm{Asin}}{{{{2\pi } \over T}{T \over 4}} \over 2} = 2{\rm{Asin}}{\pi \over 4} = A\sqrt 2 = 5\sqrt 2 cm$$
=>Chọn B
Câu hỏi 3 :
Một vật dao động điều hòa với phương trình x=8cos(4πt+π/2) cm, trong đó t đo bằng s. Khoảng thời gian trong một chu kì đầu tiên vân tốc và li độ đồng thời nhận giá trị dương là
- A 0,375s<t<0,5s.
- B 0,25s<t<0,375s.
- C 0<t<0,125s.
- D 0,125s<t<0,25s.
Đáp án: B
Lời giải chi tiết:
Câu hỏi 4 :
Một vật dao động điều hòa với biên độ A=12cm và chu kì T=0,4s. Tốc độ trung bình lớn nhất của vật trong khoảng thời gian 1/15s là
- A 1,8m/s.
- B 1,2m/s.
- C 1,5m/s.
- D 2,1m/s.
Đáp án: A
Lời giải chi tiết:
Đáp án A
Phương pháp : Áp dụng công thức tính tốc độ trung bình
\(\Delta t = {1 \over {15}} = {T \over 6}\)
Để tốc độ trung bình lớn nhất thì quãng đường đi được lớn nhất và bằng A = 12cm.
\({v_{tb}} = {{12} \over {1/15}} = 180cm/s\)
Câu hỏi 5 :
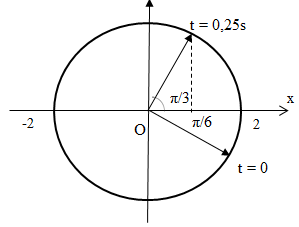
Một vật dao động điều hòa có phương trình x = 2cos(2πt – π/6) cm. Li độ của vật tại thời điểm t = 0,25 (s) là
- A 1 cm.
- B 1,5 cm
- C 0,5 cm
- D - 1 cm
Đáp án: A
Lời giải chi tiết:
Đáp án A
Phương pháp: Sử dụng vòng tròn lượng giác
Sau 0,25s => góc quét ∆φ = ω.∆t = 2π.0,25 = π/2 (rad)
=> x = 2.cosπ/3 = 1cm
Câu hỏi 6 :
Một vật dao động có gia tốc biến đổi theo thời gian: a = 8cos(20t –π/2) (m/s2). Phương trình dao động của vật là
- A x = 0,02cos(20t + π/2) (cm)
- B x = 2cos(20t – π/2) (cm)
- C x = 4cos(20t + π/2) (cm)
- D x = 2cos(20t + π/2) (cm)
Đáp án: D
Lời giải chi tiết:
Đáp án D
Phương pháp: Phương trình tổng quát của li độ và gia tốc: x = Acos(ωt+φ) (m); a = ω2Acos(ωt+φ+π) (m/s2)
Ta có: \(a = {\omega ^2}A\cos (\omega t) \Rightarrow x = Acos(\omega t - \pi )\)
Với ω = 20 rad/s; ω2A = 8m/s2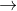 
A = 0,02m = 2cm
Phương trình dao động: x = 2cos(20t – π/2 –π) cm = 2cos(20t + π/2)cm
Câu hỏi 8 :
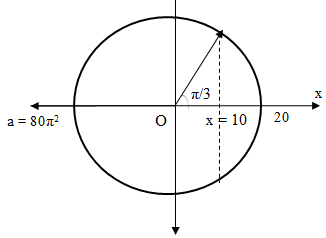
Một chất điểm dao động điều hòa với phương trình x = 20cos(2πt) cm. Gia tốc của chất điểm tại li độ x = 10 cm là
- A a = –4 m/s2
- B a = 2 m/s2
- C a = 9,8 m/s2
- D a = 10 m/s2
Đáp án: A
Phương pháp giải:
Sử dụng công thức: \(a = - {\omega ^2}x\)
Lời giải chi tiết:
Cách 1: Sử dụng công thức: \(a = - {\omega ^2}x\)
Gia tốc của chất điểm tại li độ x = 10cm là:
\(a = - {\omega ^2}x = - {\left( {2\pi } \right)^2}.10 = - 4.10.10 = - 400cm/{s^2} = - 4m/{s^2}\)
Chọn A
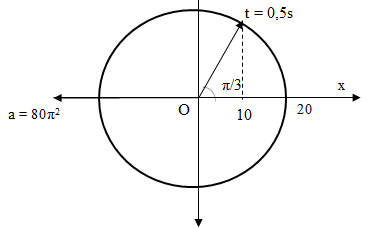
Cách 2: Sử dụng vòng tròn lượng giác
Gia tốc cực đại: a0 = 80π2 (cm/s2)
=> a = - 80π2cos(π/3) = – 4 m/s2
Chọn A
Câu hỏi 9 :
Một chất điểm dao động điều hòa trên trục Ox, với gia tốc cực đại là 320 cm/s2. Khichất điểm đi qua vị trí gia tốc có độ lớn 160 cm/s2 thì tốc độ của nó là 40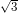
cm/s. Biên độ dao động của chất điểm là
- A 20 cm
- B 8 cm
- C 10 cm
- D 16 cm
Đáp án: A
Lời giải chi tiết:
Câu hỏi 10 :
Một vật nhỏ khối lượng 100 g, dao động điều hòa với biên độ 4 cm và tần số 5 Hz. Lấy π2=10. Lực kéo về tác dụng lên vật nhỏ có độ lớn cực đại là:
- A 8 N.
- B 4 N.
- C 2 N.
- D 6 N.
Đáp án: B
Lời giải chi tiết:
Câu hỏi 12 :
Một vật dao động điều hòa với phương trình x = 10cos(10πt) cm. Khoảng thời gian mà vật đi từ vị trí có li độ x = 5cm từ lần thứ 2015 đến lần thứ 2016 là:
- A 1/5s
- B 2/15s
- C 1/15s
- D 4/15s
Đáp án: B
Lời giải chi tiết:
Câu hỏi 13 :
Một chất điểm dao động điều hòa theo quỹ đạo thẳng dài 14 cm với chu kì 1 s. Tốc độ trung bình của chất điểm từ thời điểm t0 chất điểm qua vị trí có li độ 3,5 cm theo chiều dương đến thời điểm gia tốc của chất điểm có độ lớn cực đại lần thứ 3 (kể từ t0) là
- A 26,7 cm/s
- B 28,0 cm/s.
- C 27,3 cm/s.
- D 27 cm/s.
Đáp án: D
Lời giải chi tiết:
Câu hỏi 15 :
Chất điểm dao động điều hòa với phương trình x = 6cos(10t – 3π/2) cm. Li độ của chất điểm khi pha dao động bằng 2π/3 là
- A x = 30 cm.
- B x = 32 cm.
- C x = –3 cm.
- D x = – 40 cm.
Đáp án: C
Lời giải chi tiết:
Đáp án C
Phương pháp: Sử dụng vòng tròn lượng giác
=> Khi pha dao động bằng 2π/3 thì vật có li độ x = - 6.cos(π/3) = -3 cm
Câu hỏi 16 :
Vật DĐĐH với phương trình x=8cos25πt(cm). Biên độ, chu kì dao động của vật là:
- A 4cm;0,4s
- B 8cm;0,4s
- C 4cm;0,2s
- D 8cm;0,2s
Đáp án: C
Lời giải chi tiết:
Câu hỏi 17 :
Một chất điểm dao động điều hòa với phương trình x = 20cos(2πt) cm. Gia tốc của chất điểm tại li độ x = 10 cm là
- A a = –4 m/s2
- B a = 2 m/s2
- C a = 9,8 m/s2
- D a = 10 m/s2
Đáp án: A
Lời giải chi tiết:
Đáp án A
Phương pháp: Sử dụng vòng tròn lượng giác
=> a = -80π2.cos(π/3) = - 4m/s2
Câu hỏi 18 :
Tại thời điểm vận tốc của một vật dao động điều hoà dương và đang tăng thì
- A li độ của vật dương, gia tốc cùng hướng với chiều dương trục toạ độ.
- B li độ của vật dương, gia tốc ngược hướng với chiều dương trục toạ độ.
- C li độ của vật âm, gia tốc ngược hướng với chiều dương trục toạ độ.
- D li độ của vật âm, gia tốc cùng hướng với chiều dương trục toạ độ.
Đáp án: D
Phương pháp giải:
- Sử dụng lí thuyết về dao động điều hoà và sử dụng đường tròn lượng giác
- Vecto gia tốc luôn hướng về vị trí cân bằng
Lời giải chi tiết:
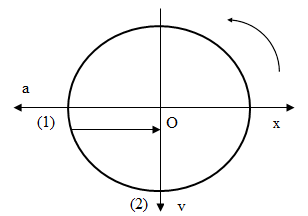
Biểu diễn trên đường tròn lượng giác:
Tại thời điểm vận tốc của một vật dao động điều hoà dương và đang tăng (từ vị trí (1) đến vị trí (2) trên đường tròn lượng giác) thì li độ của vật âm, gia tốc cùng hướng với chiều dương trục toạ độ
Câu hỏi 19 :
Hai chất điểm P, Q cùng xuất phát từ gốc và bắt đầu dao động điều hòa cùng theo trục Ox với cùng biên độ nhưng chu kì lần lượt là 3 s và 6 s. Tỉ số độ lớn vận tốc của P và Q khi chúng gặp nhau là bao nhiêu?.
- A 2:1
- B 1:2
- C 1:3
- D 3:1
Đáp án: A
Lời giải chi tiết:
Câu hỏi 20 :
Trong một dao động điều hòa có chu kì T thì thời gian ngắn nhất để vật đi từ vị trí có gia tốc cực đại đến vị trí gia tốc bằng một nửa gia tốc cực đại có giá trị là
- A T/12.
- B T/8.
- C T/6.
- D T/4.
Đáp án: C
Phương pháp giải:
Sử dụng đường tròn lượng giác
Lời giải chi tiết:
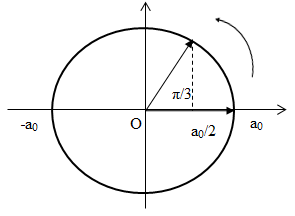
Biểu diễn trên đường tròn lượng giác ta có :
Góc quét được α = π/3
=> Thời gian ngắn nhất để vật đi từ vị trí có gia tốc cực đại đến vị trí gia tốc bằng một nửa gia tốc cực đại là :
\(\Delta t = {\alpha \over \omega } = \alpha .{T \over {2\pi }} = {\pi \over 3}.{T \over {2\pi }} = {T \over 6}\)
Câu hỏi 21 :
Một chất điểm dao động điều hòa có phương trình x=5cos(πt+π/2)(cm). Tốc độ trung bình của vật trong 2,5s
- A 5cm/s
- B 30cm/s
- C 20cm/s
- D 10cm/s
Đáp án: D
Lời giải chi tiết:
Phương trình dao động x = 5cos(πt + π/2) cm
=> Chu kì dao động T = 2π/ω = 2 s. => Thời gian t = 2,5 = T + T/4
=> Quãng đường vật đi được trong 2,5 s kể từ khi bắt đầu dao động là s = 4A + A = 5A = 25 cm
Do đó tốc độ trung bình trong khoảng thời gian đó là vtb = s/t = 25/2,5 = 10 cm/s
=> Đáp án D
Câu hỏi 22 :
Một vật dao động điều hòa trên trục Ox, giới hạn bởi một đoạn thẳng có độ dài 20 cm, tần số 0,5Hz. Gia tốc của chuyển động tại thời điểm t = 1s là \(a = \frac{1}{{\sqrt 2 }}\)(m/s2). Lấy π\(2\) = 10, phương trình dao động của vật là
- A \(x = 10\cos \left( {\pi t - \frac{{3\pi }}{4}} \right)cm\)
- B \(x = 10\cos \left( {\pi t + \frac{\pi }{4}} \right)cm\)
- C \(x = 20\cos \left( {\pi t - \frac{\pi }{4}} \right)cm\)
- D \(x = 20\cos \left( {\pi t + \frac{{3\pi }}{4}} \right)cm\)
Đáp án: B
Phương pháp giải:
Xác định A, ω và φ của phương trình x = Acos(ωt + φ)
Lời giải chi tiết:
Biên độ: A = L/2 = 10cm
Tần số góc: \(\omega = 2\pi f = \pi \)rad/s
Phương trình gia tốc: \(a = - {\pi ^2}.10c{\rm{os(}}\pi {\rm{t + }}\varphi {\rm{)}}\) (1)
Thay t = 1s và \(a = \frac{{100}}{{\sqrt 2 }}\)cm/s2 vào (1) ta tìm được \(\varphi = \frac{\pi }{4}\)rad
=> Phương trình dao động của vật: \(x = 10\cos \left( {\pi t + \frac{\pi }{4}} \right)cm\)
Câu hỏi 23 :
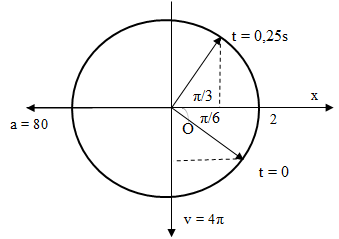
Một vật dao động điều hoà theo phương trình x = 4sin(5πt – π/6) cm. Vận tốc và gia tốc của vật ở thời điểm t = 0,5 (s) là
- A 10π
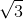cm/s và –50π2 cm/s2 - B 10π cm/s và 50
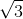π2 cm/s2 - C -10π
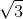cm/s và 50π2 cm/s2 - D 10π cm/s và -50
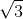π2 cm/s2.
Đáp án: D
Lời giải chi tiết:
Đáp án D
Cách 1: Dùng vòng tròn lượng giác
x = 4sin(5πt – π/6) = 4cos(5πt – 2π/3) cm
Sau 0,5s => Góc quét ∆φ = ω.∆t = 5π.0,5 = 2,5π = 2π + π/2 (rad)
=> v = 20π.cos(π/3) = 10π cm/s
a = - 100π2cos(π/6) = - 50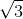
π2 cm/s2
Cách 2: Thay t vào phương trình của v và a
x = 4sin(5πt – π/6) cm
\( \Rightarrow \left\{ \matrix{ v = x' = 20\pi c{\rm{os}}(5\pi t - \pi /6) \hfill \cr a = v' = - 100{\pi ^2}\sin (5\pi t - \pi /6) \hfill \cr} \right.\)
Ở thời điểm t = 0,5s:
\( \Rightarrow \left\{ \matrix{ v = 20\pi c{\rm{os}}(5\pi .0,5 - \pi /6) = 10\pi (cm/s) \hfill \cr a = v' = - 100{\pi ^2}\sin (5\pi .0,5 - \pi /6) = - 50\sqrt 3 {\pi ^2}(cm/{s^2}) \hfill \cr} \right.\)
Câu hỏi 24 :
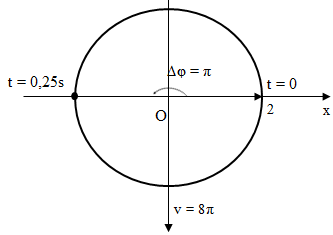
Một vật dao động điều hoà theo phương trình x = 2cos(4πt) cm. Li độ và vận tốc của vật ở thời điểm t = 0,25 (s) là
- A x = –1 cm; v = 4π cm/s.
- B x = –2 cm; v = 0 cm/s.
- C x = 1 cm; v = 4π cm/s.
- D x = 2 cm; v = 0 cm/s.
Đáp án: B
Lời giải chi tiết:
Đáp án B
Cách 1: Sử dụng vòng tròn lượng giác
Sau 0,25s => góc quét ∆φ = ω.∆t = 4π.0,25 = π (rad)
=> x = -2cm; v = 0 cm/s
Cách 2: Thay t vào phương trình của x và v
x = 2cos(4πt) cm => v = - 8π.sin(4πt) cm/s
Thay t = 0,25s vào phương của x và v:
\(\left\{ \matrix{ x = 2cos(4\pi .0,25) = - 2cm \hfill \cr v = - {\rm{ }}8\pi sin(4\pi .0,25) = 0cm/s \hfill \cr} \right.\)
Câu hỏi 25 :
Một chất điểm dao động điều hoà với phương trình dạng x = 5cos(πt + π/6) cm. Biểu thức vận tốc tức thời của chất điểm là
- A v = 5sin(πt + π/6) cm/s.
- B v = –5πsin(πt + π/6) cm/s.
- C v = – 5sin(πt + π/6) cm/s.
- D x = 5πsin(πt + π/6) cm/s.
Đáp án: B
Lời giải chi tiết:
Đáp án B
Phương pháp: v = x’
x = 5cos(πt + π/6) cm => v = x’ = –5πsin(πt + π/6) cm/s
Câu hỏi 26 :
Một chất điểm dao động điều hoà với phương trình dạng x = 5cos(πt + π/6) (cm, s). Lấy π2 = 10, biểu thức gia tốc tức thời của chất điểm là
- A a = 50cos(πt + π/6) cm/s2
- B a = – 50sin(πt + π/6) cm/s2
- C a = –50cos(πt + π/6) cm/s2
- D a = – 5πcos(πt + π/6) cm/s2
Đáp án: C
Lời giải chi tiết:
Đáp án C
Phương pháp: a = x’’
x = Acos(ωt + φ) => a = -ω2Acos(ωt + φ)
x = 5cos(πt + π/6) => a = -5π2.cos(πt + π/6) = - 50 cos(πt + π/6) cm/s2
Câu hỏi 27 :
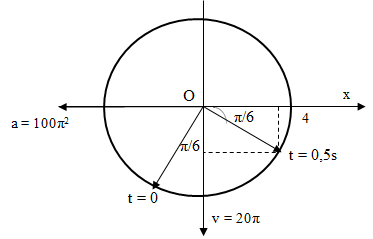
Một vật dao động điều hòa có phương trình x = 2cos(2πt – π/6) cm. Lấy π2 = 10, gia tốc của vật tại thời điểm t = 0,25 (s) là
- A 40 cm/s2
- B –40 cm/s2
- C ± 40 cm/s2
- D – π cm/s2
Đáp án: B
Lời giải chi tiết:
Đáp án B
Cách 1: Dùng vòng tròn lượng giác
Sau 0,25s => Góc quét ∆φ = ω.∆t = 2π.0,25 = 0,5π (rad)
=> a = - 80.cos(π/3) = - 40 cm/s2
Cách 2: Thay t vào phương trình của gia tốc
x = 2cos(2πt – π/6) cm => a = x’’ = - 80.cos(2πt – π/6) cm/s2
Thời điểm t = 0,25s => a = - 80.cos(2π.0,25 – π/6) = - 40 cm/s2
Câu hỏi 28 :
Một vật dao động điều hòa có phương trình x = 5cos(2πt – π/6) cm. Vận tốc của vật khi có li độ x = 3 cm là
- A v = 25,12 cm/s.
- B v = ± 25,12 cm/s.
- C v = ± 12,56 cm/s
- D v = 12,56 cm/s.
Đáp án: B
Lời giải chi tiết:
Đáp án B
Phương pháp: Sử dụng vòng tròn lượng giác
Vận tốc cực đại: v0 = 10π cm/s
Ta có cosα = 3/5 ; \(v = \pm {v_0}.cos\left( {{\pi \over 2}-{\rm{ }}\alpha } \right) = \pm 10\pi cos\left( {{\pi \over 2}-\alpha } \right) = \pm 25,12cm/s\)
Câu hỏi 29 :
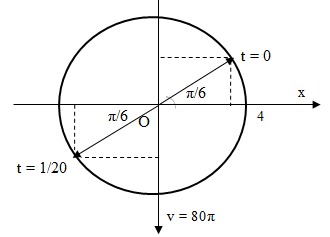
Một vật dao động điều hòa với phương trình x = 4cos(20πt + π/6) cm. Chọn phát biểu đúng ?
- A Tại t = 0, li độ của vật là 2 cm.
- B Tại t = 1/20 (s), li độ của vật là 2 cm.
- C Tại t = 0, tốc độ của vật là 80 cm/s.
- D Tại t = 1/20 (s), tốc độ của vật là 125,6 cm/s.
Đáp án: D
Lời giải chi tiết:
Đáp án D
Phương pháp : Sử dụng vòng tròn lượng giác
+ Tại t = 0 : x = 2.cos(π/6) =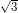 
cm ; v = - 80π.cos(π/3) = - 40π cm/s
+ Sau 1/20 s => góc quét ∆φ = ω.∆t = 20π. (1/20) = π rad
=> x = - 2. cos(π/6) = -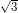 cm; v = 80π.cos(π/3) = 125,6 cm/s
Câu hỏi 30 :
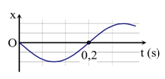
Một vật dao động điều hòa trên trục Ox. Hình bên là đồ thị biểu diễn sự phụ thuộc của li độ x vào thời gian t . Tần số góc của dao động là
- A 10 rad/s
- B 10π rad/s.
- C 5π rad/s.
- D 5 rad/s.
Đáp án: C
Lời giải chi tiết:
Đáp án C
Phương pháp: Áp dụng công thức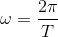 
kết hợp kĩ năng đọc đồ thị
Từ đồ thị ta có: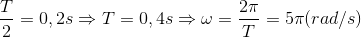 
Câu hỏi 31 :
Một chất điểm dao động điều hoà có đồ thị biểu diễn sự phụ thuộc của li độ x vào thời gian t như hình vẽ. Tại thời điểm t = 0,2s, chất điểm có li độ 2cm. Ở thời điểm t = 0,9s, gia tốc của chất điểm có giá trị bằng
- A 14,5 cm/ s2.
- B 0,57m/ s2.
- C 5,70 m/ s2.
- D 1,45 m/ s2.
Đáp án: B
Phương pháp giải:
Sử dụng phương trình li độ và gia tốc của dao động điều hoà, kết hợp kĩ năng đọc đồ thị.
Lời giải chi tiết:
+ Phương trình của li độ và gia tốc:
\(\left\{ \matrix{
x = Ac{\rm{os}}\left( {\omega t + \varphi } \right) \hfill \cr
a = - {\omega ^2}Ac{\rm{os}}\left( {\omega t + \varphi } \right) \hfill \cr} \right.\)
+ Từ đồ thị ta thấy: T/2 = 8ô, 1ô = 0,1s T = 1,6s \( \Rightarrow \omega = {{5\pi } \over 4}rad/s\)
+ Tại t = 0,3s có x = 0 \(\Leftrightarrow A\cos \left( {{{5\pi } \over 4}t + \varphi } \right) = 0 \Rightarrow \varphi = {\pi \over 8}rad\)
+ Tại t = 0,2s có x = 2cm \(\Leftrightarrow A\cos \left( {{{5\pi } \over 4}.0,2 + {\pi \over 8}} \right) = 2 \Rightarrow A = 5,226cm\)
=> Phương trình của gia tốc: \(a = - {\left( {{{5\pi } \over 4}} \right)^2}.5,226.c{\rm{os}}\left( {{{5\pi } \over 4}t + {\pi \over 8}} \right)\)
+ Tại t = 0,9s \( \Rightarrow a = - {\left( {{{5\pi } \over 4}} \right)^2}.5,226.c{\rm{os}}\left( {{{5\pi } \over 4}.0,9 + {\pi \over 8}} \right) = 0,57m/{s^2}\)
Chọn B
Câu hỏi 32 :
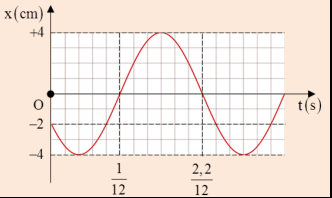
Hình vẽ là đồ thi biễu diễn độ dời của dao động x theo thời gian t của một vật dao động điều hòa. Phương trình dao động của vật là 
- A
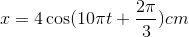
- B
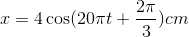
- C
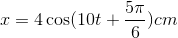
- D
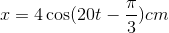
Đáp án: A
Lời giải chi tiết:
Từ đồ thị ta thấy: \({T \over 2} = {{2,2} \over {12}} - {1 \over {12}} = {{1,2} \over {12}} \Rightarrow T = 0,2s \Rightarrow \omega = {{2\pi } \over T} = 10\pi \left( {rad/s} \right)\)
Tại thời điểm t = 0:
\(\eqalign{
& \left\{ {{x_0} = - 2cm \Leftrightarrow \left\{ \matrix{
4\cos \varphi = - 2 \hfill \cr
\sin \varphi > 0 \hfill \cr} \right.} \right. \Rightarrow \varphi = {{2\pi } \over 3}rad \cr
& \Rightarrow x = 4\cos \left( {10\pi t + {{2\pi } \over 3}} \right)cm \cr} \)
Câu hỏi 33 :
Cho 3 vật dao động điều hòa lần lượt có biên độ A1 = 5cm, A2 = 10 cm, A3 = 5\(\sqrt 2 \) cm và tần số f1, f2, f3. Biết rằng tại mọi thời điểm, li độ và vận tốc của các vật liên hệ bằng biểu thức \(\frac{{{x_1}}}{{{v_1}}} + \frac{{{x_2}}}{{{v_2}}} = \frac{{{x_3}}}{{{v_3}}}\) . Tại thời điểm t, các vật cách VTCB của chúng những đoạn lần lượt là 4 cm, 8cm và x0. Giá trị của x0 gần giá trị nào nhất sau đây
- A 3cm
- B 2cm
- C 6,4 cm
- D 4cm
Đáp án: C
Phương pháp giải:
Sử dụng công thức độc lập với thời gian kết hợp với đạo hàm
Lời giải chi tiết:
Theo đề bài ta có \(\frac{{{x_1}}}{{{v_1}}} + \frac{{{x_2}}}{{{v_2}}} = \frac{{{x_3}}}{{{v_3}}}\) , đạo hàm hai vế của phương trình trên ta được:
\(\begin{array}{l}\frac{{v_1^2 - {a_1}{x_1}}}{{v_1^2}} + \frac{{v_2^2 - {a_2}{x_2}}}{{v_2^2}} = \frac{{v_3^2 - {a_3}{x_3}}}{{v_3^2}} \Leftrightarrow \frac{{v_1^2 + \omega _1^2x_1^2}}{{v_1^2}} + \frac{{v_2^2 + \omega _2^2x_2^2}}{{v_2^2}} = \frac{{v_3^2 + \omega _3^2x_3^2}}{{v_3^2}}\\ \Leftrightarrow 1 + \frac{{x_1^2}}{{\frac{{v_1^2}}{{\omega _1^2}}}} + \frac{{x_2^2}}{{\frac{{v_2^2}}{{\omega _2^2}}}} = \frac{{x_3^2}}{{\frac{{v_3^2}}{{\omega _3^2}}}} \Leftrightarrow 1 + \frac{{x_1^2}}{{A_1^2 - x_1^2}} + \frac{{x_2^2}}{{A_2^2 - x_2^2}} = \frac{{x_3^2}}{{A_3^2 - x_3^2}}(*)\end{array}\)
Theo đề bài cho A1 = 5cm, A2 = 10 cm, A3 = 5\(\sqrt 2 \) cm; tại thời điểm t ta có: \(\left| {{x_1}} \right| = 4cm;\left| {{x_2}} \right| = 8cm\)
Thay vào biểu thức (*) ta tính được x0 = x3 = 6,4(cm)
Câu hỏi 34 :
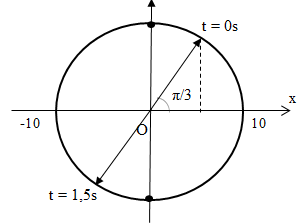
Hai chất điểm A và B dao động điều hòa với cùng biên độ. Thời điểm ban đầu t = 0 hai chất điểm đều đi qua vị trí cân bằng theo chiều dương. Biết chu kỳ dao động của chất điểm A và B lần lượt là T và 0,5T. Tại thời điểm t = T/12 tỉ số giữa tốc độ của chất điểm A và tốc độ của chất điểm B là
- A 1/2
- B
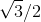
- C
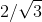
- D 2
Đáp án: B
Lời giải chi tiết:
Câu hỏi 35 :
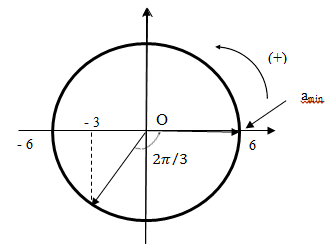
Một vật dao động điều hoà trên trục Ox với biên độ 6 cm, chu kì bằng ls. Tại thời điểm ban đầu vật có li độ -3 cm đang đi về vị trí cân bằng. Kể từ thời điểm ban đầu đến lúc mà giá trị đại số của gia tốc của vật đạt cực tiểu lần thứ 3 thì tốc độ trung bình của vật trong khoảng thời gian đó là
- A 24,43 cm/s
- B 24,35 cm/s
- C 24,75 cm/s
- D 24,92 cm/s
Đáp án: A
Phương pháp giải:
Sử dụng vòng tròn lượng giác và công thức tính tốc độ trung bình
Lời giải chi tiết:
Ta có giá trị đại số của a cực tiểu thì x = A
Quãng đường vật đi được: S = A/2 + A + 2.4A = 57cm
Thời gian vật đi: t = T/3 +2T = 7/3 s
Tốc độ trung bình là: v = S/t =24,43 cm/s
Câu hỏi 36 :
Một vật dao động điều hòa dọc theo trục Ox. Biết trong thời gian 20 s thì vật thực hiện được 50 dao động toàn phần và vận tốc cực đại bằng 20π cm/s. Nếu chọn gốc thời gian lúc vật đi qua vị trí cân bằng theo chiều âm thì phương trình dao động của vật là:
- A
- B
- C
- D
Đáp án: D
Lời giải chi tiết:
Câu hỏi 37 :
Hai điểm sáng M và N dao động điều hòa cùng biên độ trên trục Ox, tại thời điểm ban đầu hai chất điểm cùng đi qua vị trí cân bằng theo chiều dương. Chu kỳ dao động của M gấp 5 lần chu kỳ dao động của N. Khi hai chất điểm ngang nhau lần thứ nhất thì M đã đi được 10 cm. Quãng đường đi được của N trong khoảng thời gian đó bằng
- A 50cm
- B 30 cm
- C 25 cm
- D 40 cm
Đáp án: B
Lời giải chi tiết:
Câu hỏi 38 :
Xét dao động điều hòa với A = 2 cm và tần số f. Khoảng thời gian ngắn nhất để vận tốc của vật thay đổi từ 2π cm/s đến -2π\(\sqrt3\) cm/s là T/4. Tìm f.
- A 1 Hz.
- B 0,5 Hz.
- C 5 Hz.
- D 2 Hz.
Đáp án: A
Lời giải chi tiết:
Câu hỏi 39 :
Một vật nhỏ dao động điều hòa dọc theo trục Ox với biên độ 5cm, chu kỳ 2s. Tại thời điểm t = 0, vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động của vật là
- A x = 5cos(2πt – π/2) (cm)
- B x = 5cos(2πt + π/2) (cm)
- C x = 5cos(πt – π/2) (cm)
- D x = 5cos(2πt + π/2) (cm)
Đáp án: C
Phương pháp giải:
Phương pháp: Viết phương trình dao động điều hòa.
Bước 1: Tìm A:
Bước 2: Tìm ω: $$\omega = \sqrt {{k \over m}} = 2\pi f = {{2\pi } \over T}$$
Bước 3: Tìm φ:
Tại t=0:
$$\left\{ \matrix{ x = Ac{\rm{os}}\varphi \hfill \cr {\rm{v = - A}}\omega {\rm{sin}}\varphi \hfill \cr} \right. \to \left\{ \matrix{ {\rm{cos}}\varphi {\rm{ = }}{{{x_0}} \over A} \hfill \cr \sin \varphi = - {v \over {A\omega }} \hfill \cr} \right. \to \varphi = ?$$
Lời giải chi tiết:
Đáp án C
Ta có: A = 5 cm
$$\omega = {{2\pi } \over T} = \pi {\rm{ }}rad/s$$
Tại t=0:
$$\left\{ \matrix{ x = Ac{\rm{os}}\varphi = 0 \hfill \cr {\rm{v = - A}}\omega {\rm{sin}}\varphi > 0 \hfill \cr} \right. \to \left\{ \matrix{ {\rm{cos}}\varphi {\rm{ = 0}} \hfill \cr \sin \varphi < 0 \hfill \cr} \right. \to \varphi = - {\pi \over 2}$$
=>x = 5cos(πt – π/2)
Câu hỏi 40 :
Một vật dao động điều hòa với phương trình x = 10cos(2πt + π/3) cm. Trong 1,5 (s) kể từ khi dao động (t = 0) thì vật qua vị trí cân bằng mấy lần?
- A 2 lần.
- B 3 lần.
- C 4 lần.
- D 5 lần.
Đáp án: B
Lời giải chi tiết:
Đáp án B
Phương pháp: Sử dụng vòng tròn lượng giác
Sau 1,5s => góc quét ∆φ = ω.∆t = 2π.1,5 = 3π rad
Chất điểm quét được góc 2π => vật đi qua VTCB 2 lần
=> Chất điểm quét góc 3π => vật đi qua VTCB 3 lần.
Câu hỏi 41 :
Một vật dao động điều hòa với biên độ A và chu kỳ T. Trong khoảng thời gian ∆t = 5T/6, quãng đường nhỏ nhất (Smin) mà vật đi được là
- A A\(\root \of 3 \)
- B A + A\(\root \of 3 \)
- C 2A + A\(\root \of 3 \)
- D 3A.
Đáp án: D
Phương pháp giải:
Sử dụng đường tròn lượng giác
Lời giải chi tiết:
Ta có: \(\Delta t = {{5T} \over 6} = {T \over 2} + {T \over 3} \Rightarrow {S_{\min }} = 2A + {S_{\min T/3}}\)
=> Góc quét được trong khoảng thời gian T/3 là 2π/3.
Quãng đường vật đi được trong ½ chu kì là 2A.
+ Vật có v = 0 khi qua vị trí biên => Trong cùng một khoảng thời gian vật đi được quãng đường nhỏ nhất khi đi xung quanh vị trí biên. Biểu diễn trên đường lượng giác ta có:
\( \Rightarrow {S_{\min {\rm{T/3}}}} = {A \over 2} + {A \over 2} = A \Rightarrow {S_{\min }} = 2A + {S_{\min T/3}} = 2A + A = 3A\)
Câu hỏi 42 :
Một vật dao động điều hòa với biên độ A và chu kỳ T. Trong khoảng thời gian ∆t = 5T/6, quãng đường lớn nhất (Smax) mà vật đi được là
- A A + A\(\root \of 3 \).
- B 4A - A\(\root \of 3 \)
- C 2A + A\(\root \of 3 \)
- D 2A\(\root \of 3 \)
Đáp án: C
Phương pháp giải:
Sử dụng đường tròn lượng giác
Lời giải chi tiết:
Ta có: \(\Delta t = {{5T} \over 6} = {T \over 2} + {T \over 3} \Rightarrow {S_{m{\rm{ax}}}} = 2A + {S_{\max T/3}}\)
=> Góc quét được trong khoảng thời gian T/3 là 2π/3.
Quãng đường vật đi được trong ½ chu kì là 2A.
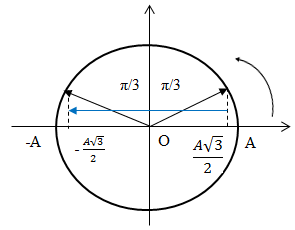
Vật có tốc độ cực đại khi qua vị trí cân bằng. Trong cùng một khoảng thời gian vật đi được quãng đường lớn nhất khi đi xung quanh vị trí cân bằng. Biểu diễn trên đường tròn lượng giác:
\( \Rightarrow {S_{m{\rm{axT/3}}}} = {{A\sqrt 3 } \over 2} + {{A\sqrt 3 } \over 2} = A\sqrt 3 \Rightarrow {S_{m{\rm{ax}}}} = 2A + {S_{\max T/3}} = 2A + A\sqrt 3 \)
Câu hỏi 43 :
Một vật dao động điều hòa với biên độ A và chu kỳ T. Trong khoảng thời gian ∆t = 3T/4, quãng đường lớn nhất (Smax) mà vật đi được là
- A 2A - A\(\root \of 2 \).
- B 2A + A\(\root \of 2 \).
- C 2A\(\root \of 3 \).
- D A + A\(\root \of 2 \).
Đáp án: B
Phương pháp giải:
Sử dụng đường tròn lượng giác
Lời giải chi tiết:
Ta có: \(\Delta t = {{3T} \over 4} = {T \over 2} + {T \over 4} \Rightarrow {S_{m{\rm{ax}}}} = 2A + {S_{\max T/4}}\)
=> Góc quét được trong khoảng thời gian T/4 là π/2.
Quãng đường vật đi được trong ½ chu kì là 2A.
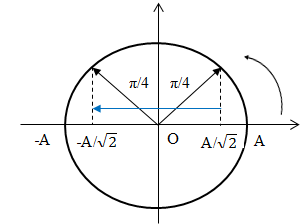
Vật có tốc độ cực đại khi qua vị trí cân bằng. Trong cùng một khoảng thời gian vật đi được quãng đường lớn nhất khi đi xung quanh vị trí cân bằng. Biểu diễn trên đường tròn lượng giác:
\( \Rightarrow {S_{m{\rm{axT/4}}}} = {5 \over {\sqrt 2 }} + {5 \over {\sqrt 2 }} = 5\sqrt 2 cm \Rightarrow {S_{m{\rm{ax}}}} = 2A + {S_{\max T/4}} = 2A + {A \over {\sqrt 2 }} + {A \over {\sqrt 2 }} = 2A + A\sqrt 2 \)
Câu hỏi 44 :
Một chất điểm dao động điều hòa với chu kỳ là 1 s. Tại thời điểm t =1/3 s kể từ thời điểm ban đầu, chất điểm cách biên âm 4 cm và chuyển động theo chiều âm. Tại thời điểm t = 2/3 s, chất điểm bắt đầu đổi chiều chuyển động lần thứ hai. Vận tốc của chất điểm tại thời điểm t = 2018,75 s có giá trị gần nhất với giá trị nào sau đây?
- A 22 cm/s.
- B – 25 cm/s.
- C 50 cm/s
- D – 22 cm/s.
Đáp án: C
Lời giải chi tiết:
Đáp án C
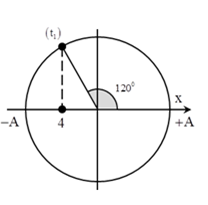
+ Tại thời điểm \({t_1} = {1 \over 3}\) chất điểm cách biên âm 4 cm và có vận tốc đang tăng, đến thời điểm \({t_2} = {2 \over 3}\,\,s\) chất điểm đổi chiều lần thứ hai (lần thứ hai đi qua vị trí biên).
=> Từ hình vẽ ta dễ thấy rằng \(0,5{\rm{A}} = 4\,\,cm \to A = 8\,\,cm\) và ban đầu chất điểm ở biên dương.
+ Sau 2018 s chất điểm quay trở lại biên dương, sau 0,75 s nữa chất điểm đi qua vị trí cân bằng theo chiều dương.
\( \to v = {v_{\max }} = \omega A = 16\pi \approx 50,26\,\,{cm/s}\)
Câu hỏi 45 :
Một vật nhỏ dao động điều hòa trên trục Ox với chu kì 2s, biên độ 6cm. Tại thời điểm t, vật có li độ -3cm đang chuyển động nhanh dần đều thời điểm mà gia tốc của vật có giá trị cực tiểu lần thứ 3 thì tốc độ trung bình của vật gần nhất với giá trị nào sau đây?
- A 12,8 cm/s
- B 12,6 cm/s
- C 12,4 cm/s
- D 12,2 cm/s
Đáp án: C
Phương pháp giải:
Sử dụng công thức tính tốc độ trung bình: vtb = S/t
Lời giải chi tiết:
Ta có: T = 2s, A = 6cm.
Tại t:
\(\left\{ \matrix{
x = - 3cm \hfill \cr
v > 0 \hfill \cr} \right.\)
Tại vị trí gia tốc cực tiểu => x = A
Tốc độ trung bình: \({v_{tb}} = {S \over t} = {{0,5A + 5{\rm{A}}} \over {{T \over {12}} + {{5T} \over 4}}} = {{5,5{\rm{A}}} \over {{{4T} \over 3}}} = 12,375cm/s\)
=> Chọn C
Câu hỏi 46 :
Một vật nhỏ dao động điều hoà trên trục Ox với chu kì T = 2s. Gốc O trùng vị trí cân bằng. Tại thời điểm t1 vật có li độ x1, tại thời điểm t2 = t1 + 0,5s vận tốc của vật có giá trị là v2 = b. Tại thời điểm t3 = t2 + 1s vận tốc của vật có giá trị v3 = b + 8π cm/s. Li độ x1 có độ lớn gần giá trị nào nhất sau đây
- A 3,5cm
- B 4,2cm
- C 4,8m
- D 5,5cm
Đáp án: B
Phương pháp giải:
Phương pháp: Thay t vào phương trình của li độ và vận tốc
Lời giải chi tiết:
Đáp án B
Câu hỏi 47 :
Một chất điểm dao động điều hòa trên trục tọa độ Ox với biên độ 10 cm và đạt gia tốc cực đại tại li độ x1. Sau đó, vật lần lượt đi qua các điểm có li độ x2, x3, x4, x5, x6, x7 trong những khoảng thời gian bằng nhau Δt = 0,1 s. Biết thời gian vật đi từ x1 đến x7hết một nửa chu kỳ dao động. Khoảng cách lớn nhất giữa hai điểm gần nhau liên tiếp là
- A 5 cm.
- B 4 cm.
- C \(4\sqrt 2 cm\)
- D \(5\sqrt 2 cm\)
Đáp án: A
Lời giải chi tiết:
Đáp án A
+ Gia tốc của vật cực đại tại vị trí biên âm \(\to {x_1} = - A\).
Vật đi từ \({{\rm{x}}_1} \to {x_7}\) hết nửa chu kì, vậy \({{\rm{x}}_7} = + A \to \) các vị trí liên tiếp các nhau ứng với góc quét \(30^\circ \to \Delta {x_{\max }} = 0,5A = 5\,\,cm\).
Câu hỏi 48 :
Một vật nhỏ dao động điều hòa trên đoạn MN = 12 cm. Tại vị trí cách M một đoạn 2 cm, vật có tốc độ 70,25 cm/s. Tần số dao động của vật bằng
- A 2Hz
- B 2,5Hz
- C 4Hz
- D 5Hz
Đáp án: B
Phương pháp giải:
Sử dụng hệ thức độc lập theo thời gian: \({A^2} = {x^2} + {{{v^2}} \over {{\omega ^2}}}\)
Lời giải chi tiết:
Ta có: A = MN/2 = 6cm
Tại vị trí cách M 1 đoạn 2cm => x= 6-2= 4cm
\({A^2} = {x^2} + {{{v^2}} \over {{\omega ^2}}} \leftrightarrow {6^2} = {4^2} + {{{{70,25}^2}} \over {{\omega ^2}}} \to \omega = 15,7{\rm{r}}a{\rm{d}}/s \to f = {\omega \over {2\pi }} \approx 2,5H{\rm{z}}\)
=> Chọn B
Câu hỏi 49 :
Một vật dao động điều hòa theo phương trình x = 10cos10πt(cm). Vân tốc của vật có độ lớn bằng 50π (cm/s) lần thứ 2017 kể từ lúc t = 0 tại thời điểm:
- A 6048/60 s.
- B 6049/60 s.
- C 6047/60 s.
- D 605/6 s.
Đáp án: B
Lời giải chi tiết:
Câu hỏi 50 :
Một vật dao động theo phương trình x = 20cos(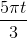
- 
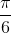) (cm; s). Kể từ lúc t = 0 đến lúc vật qua li độ - 10 cm theo chiều âm lần thứ 2017 thì lực hồi phục sinh công âm trong khoảng thời gian:
- A 1210,4s.
- B 1209,8s.
- C 3226,4s
- D 2414,6 s.
Đáp án: B
Lời giải chi tiết:
