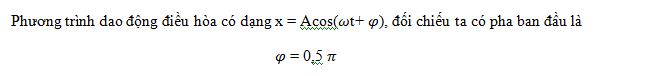Câu hỏi 1 :
Một chất điểm dao động điều hòa trên đoạn thẳng có chiều dài quỹ đạo L. Biên độ của dao động là:
- A 2L.
- B L/2.
- C L.
- D L/4.
Đáp án: B
Phương pháp giải:
Áp dụng công thức tính chiều dài quỹ đạo trong dao động điều hòa
Lời giải chi tiết:
Ta có quỹ đạo của vật dao động điều hòa là một đoạn thẳng có chiều dài l = 2A
Theo đề bài: l = L = 2A → A = L/2.
Câu hỏi 2 :
Một vật nhỏ dao động theo phương trình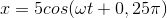 
cm. Pha của dao động là
- A 0,125
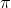
- B 0,5
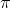
- C 0,25
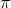
- D ωt + 0,25π
Đáp án: D
Phương pháp giải:
Phương trình x = Acos(ωt + φ) với (ωt + φ) là pha của dao động
Lời giải chi tiết:
Pha của dao động : ωt + 0,25π
Chọn D
Câu hỏi 3 :
Vật dao động điều hòa có phương trình x = Acos(wt + j). Gọi v và a lần lượt là vận tốc và gia tốc của vật. Hệ thức đúng là
- A
- B
- C
- D
Đáp án: C
Câu hỏi 4 :
Vật dao động điều hòa với phương trình: x = 8cos(πt + π/6)cm. Pha ban đầu của dao động là
- A π/6rad.
- B - π/6rad.
- C (πt + π/6)rad.
- D π/3rad.
Đáp án: A
Câu hỏi 5 :
Một chất điểm dao động điều hòa dọc theo trục Ox với phương trình x =10cos 2π t (cm). Quãng đường đi được của chất điểm trong một chu kì dao động là
- A 20 cm.
- B 40 cm.
- C 10 cm.
- D 30 cm.
Đáp án: B
Phương pháp giải:
Áp dụng công thức tính quãng đường đi được của vật dao động điều hòa trong một chu kì
Lời giải chi tiết:
Áp dụng công thức tính quãng đường đi được của vật dao động điều hòa trong một chu kì
Ta có S = 4A = 40cm
Câu hỏi 6 :
Một chất điểm dao động điều hòa với phương trình x=6cosπt ( x tính bằng cm, t tính bằng s). Phát biểu nào sau đây đúng?
- A Tốc độ cực đại của chất điểm là 18,8 cm/s.
- B Tần số của dao động là 2 Hz.
- C Chu kì của dao động là 0,5 s.
- D Gia tốc của chất điểm có độ lớn cực đại là 113 cm/s2.
Đáp án: A
Lời giải chi tiết:
Câu hỏi 8 :
Một vật nhỏ dao động điều hòa theo một quỹ đạo dài 8cm. Dao động này có biên độ là:
- A 16cm
- B 8cm
- C 48cm
- D 4cm
Đáp án: D
Lời giải chi tiết:
Quỹ đạo của vật dao động điều hòa l = 2A = 8 cm => A = 4cm
=> Chọn D
Câu hỏi 9 :
Khi một vật dao động điều hòa, chuyển động của vật từ vị trí cân bằng ra vị trí biên là chuyển động
- A nhanh dần đều.
- B chậm dần đều.
- C nhanh dần.
- D chậm dần.
Đáp án: D
Lời giải chi tiết:
Đáp án D
Câu hỏi 10 :
Một vật dao động điều hòa với phương trình x = 4cos(2πt + π/2)cm. Vận tốc cực đại của vật trong quá trình dao động bằng
- A 2πcm/s.
- B - 8πcm/s.
- C 8πcm/s.
- D 4πcm/s.
Đáp án: C
Lời giải chi tiết:
Câu hỏi 11 :
Một vật dao động điều hòa trên trục Ox với O trùng vị trí cân bằng, biên độ dao động 10 cm, chu kì dao động là T = 2 s. Chọn gốc thời gian (t = 0) là lúc vật đi qua vị trí cân bằng theo chiều dương, phương trình dao động của vật là
- A x = 10cos(πt – 0,5π) cm.
- B x = 10cos(πt + π) cm.
- C x = 10cos(πt + 0,5π) cm.
- D x = 10cos(πt) cm.
Đáp án: A
Phương pháp giải:
Công thức liên hệ giữa tần số góc và chu kỳ dao động trong dao động cơ.
Lời giải chi tiết:
Đáp án A
+ Tần số góc của dao động $$\omega = {{2\pi } \over T} = \pi \,rad/s$$
Phương trình dao động của vật x = 10cos(πt – 0,5π) cm.
Câu hỏi 12 :
Vật dao động điều hòa theo phương trình x = 4cos(πt + φ) cm. Tại thời điểm ban đầu vật có li độ 2 cm và đang chuyển động ngược chiều dương của trục tọa độ. Pha ban đầu của dao động điều hòa là
- A $${\pi \over 3} rad$$
- B $$-{\pi \over 3} rad$$
- C $${\pi \over 6} rad$$
- D $$-{\pi \over 6} rad$$
Đáp án: A
Lời giải chi tiết:
Đáp án A
+ Pha ban đầu của dao động $$\varphi = {\pi \over 3}$$.
Câu hỏi 13 :
Một chất điểm dao động điều hòa với phương trình x=2cos(2πt)(x tính bằng cm, t tính bằng s). Tốc độ lớn nhất của chất điểm trong quá trình dao động là
- A 4π cm/s.
- B π cm/s.
- C 3π cm/s.
- D 2π cm/s.
Đáp án: A
Lời giải chi tiết:
Phương pháp: Áp dụng công thức tính tốc độ cực đại trong dao động điều hòa
Tốc độ cực đại của chất điểm vmax = ωA = 2π.2 = 4π cm/s => Chọn A
Câu hỏi 14 :
Một vật dao động điều hòa có phương trình x = 4cos(10t – 0,25π) cm. Biên độ dao động của vật là
- A 8 cm.
- B 16 cm.
- C 0 cm.
- D 4 cm.
Đáp án: D
Phương pháp giải:
Công thức tính li độ của vật ở thời điểm t :$$x = A\cos \left( {\omega t + \varphi } \right)$$
Lời giải chi tiết:
Đáp án D
+ Biên độ dao động của vật A = 4 cm.
Câu hỏi 15 :
Chọn đáp án sai khi nói về dao động cơ điều hòa với biên độ A.
- A Khi vật đi từ vị trí cân bằng ra biên thì chiều của vận tốc ngược với chiều của gia tốc.
- B Khi vật đi từ vị trí cân bằng ra biên thì độ lớn của gia tốc tăng.
- C Quãng đường vật đi được trong một phần tư chu kì dao động là A.
- D Khi vật đi từ biên về vị trí cân bằng thì chiều của vận tốc cùng với chiều của gia tốc.
Đáp án: C
Lời giải chi tiết:
Đáp án C
+ Quãng đường vật đi được trong một phần tư chu kì tùy vào vào vị trí của vật → có thể khác A → C sai.
Câu hỏi 16 :
Một vật dao động điều hòa với tần số 2,5 Hz và có biên độ 0,020 m. Vận tốc cực đại của nó bằng
- A 0,008 m/s.
- B 0,050 m/s.
- C 0,125 m/s.
- D 0,314 m/s.
Đáp án: D
Lời giải chi tiết:
Đáp án D
+ Vận tốc cực đại vmax = 2πfA = 0,314 m/s.
Câu hỏi 17 :
Xét dao động điều hòa của con lắc đơn tại một điểm trên mặt đất. Khi con lắc đơn đi từ vị trí biên về vị trí cân bằng thì
- A độ lớn li độ tăng.
- B tốc độ giảm.
- C độ lớn lực phục hồi giảm.
- D thế năng tăng.
Đáp án: C
Phương pháp giải:
Phương pháp : Đại cương về dao động điều hòa
Lời giải chi tiết:
Đáp án C
+ Khi con lắc đi từ vị trí biên về vị trí cân bằng thì độ lớn của lực phục hồi giảm.
Câu hỏi 18 :
Một vật nhỏ dao động điều hòa theo phương trình x = Acos(10πt + 0,5π) (t tính bằng s). Tần số dao động của vật là:
- A 10 Hz.
- B 10π Hz.
- C 5π Hz.
- D 5 Hz.
Đáp án: D
Lời giải chi tiết:
Đáp án D
Tần số dao động của vật là f = 5 Hz
Câu hỏi 19 :
Một vật dao động điều hoà có phương trình x = 4cos(20πt – π/6) cm . Tần số và pha ban đầu của dao động lần lượt là
- A 10Hz và -π/6 rad .
- B 1/10Hz và π/6 rad.
- C 1/10Hz và –π/6 rad.
- D 10Hz và π/6 rad.
Đáp án: A
Lời giải chi tiết:
Đáp án A
Phương pháp: Sử dụng lí thuyết về phương trình dao động điều hoà
ω = 20π rad/s --> f = 10Hz, pha ban đầu φ = - π/6 rad
Câu hỏi 20 :
Một vật dao động điều hòa trên quỹ đạo 8 cm với tần số 2 Hz. Tính thời gian ngắn nhất vật đi từ x = 2 cm đến x = -2 cm:
- A 0,083 s.
- B 0,17 s.
- C 0,25 s.
- D 0,33 s.
Đáp án: A
Lời giải chi tiết:
Đáp án A
Biên độ dao động của vật A = 0,5L = 4 cm.
+ Thời gian ngắn nhất khi vật chuyển động giữa hai vị trí xung quanh vị trí cân bằng.
→ Thời gian ngắn nhất $$\Delta t = {T \over 6} = 0,083 s $$.
Câu hỏi 21 :
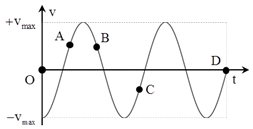
Một vật dao động điều hòa có đồ thị vận tốc như hình vẽ. Nhận định nào sau đây đúng?
- A Li độ tại Α và Β giống nhau
- B Vận tốc tại C cùng hướng với lực hồi phục.
- C Tại D vật có li độ cực đại âm.
- D Tại D vật có li độ bằng 0.
Đáp án: C
Phương pháp giải:
Phương pháp: Vận tốc luôn dao động vuông pha với li độ
Lời giải chi tiết:
Đáp án C
+ Tại D vật có li độ cực đại âm.
Câu hỏi 22 :
Một chất điểm dao động điều hòa với phương trình: x=5cos(2πt) cm. Tọa độ của chất điểm t=1,5s là
- A x=-5cm.
- B x=1,5cm.
- C x=0cm.
- D x=5cm.
Đáp án: A
Phương pháp giải:
Thay t vào phương trình của x
Lời giải chi tiết:
Ta có :\(x = 5.c{\rm{os}}(2\pi .1,5) = - 5cm\)
Chọn A
Câu hỏi 23 :
Một chất điểm dao động điều hòa với biên độ A, tần số góc ω. Tại thời điểm vật chuyển động qua vị trí có li độ x, khi đó vật có gia tốc là a. Mối liên hệ giữa x, a, ω và A là
- A x=-ω2a.
- B \({A^2} = {x^2} + {{{a^2}} \over {{\omega ^4}}}\)
- C \({A^2} = {x^2} + {\left( {{a \over \omega }} \right)^2}\)
- D a=-ω2x
Đáp án: D
Phương pháp giải:
Sử dụng hệ thức độc lập theo thời gian của x, v, a
Lời giải chi tiết:
a = - ω2x
Chọn D
Câu hỏi 24 :
Một chất điểm dao động điều hòa theo phương trình x = Acos(ωt + 0,5π). Mốc thời gian được chọn là lúc chất điểm:
- A qua vị trí cân bằng theo chiều dương.
- B qua li độ 0,5A theo chiều dương.
- C qua li độ 0,5A theo chiều âm.
- D qua vị trí cân bằng theo chiều âm.
Đáp án: D
Lời giải chi tiết:
Đáp án D
Mốc thời gian được chọn là lúc vật đi qua vị trí cân bằng theo chiều âm
Câu hỏi 25 :
Vật dao động điều hòa với biên độ A, chu kì T. Tại thời điểm ban đầu vật đang ở vị trí biên âm (x = -A). Thời điểm đầu tiên vật đi qua vị trí cách vị trí cân bằng 0,5A là
- A T/4.
- B T/6.
- C T/3.
- D T/12.
Đáp án: B
Phương pháp giải:
Sử dụng vòng tròn lượng giác
Lời giải chi tiết:
Ta biểu diễn dao động của vật trên vòng tròn lượng giác như hình vẽ
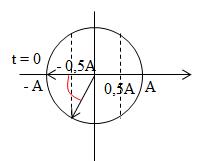
Từ hình vẽ ta thấy t = T/ 6
Chọn B
Câu hỏi 26 :
Một vật dao động điều hoà chuyển động từ vị trí cân bằng về biên. Nhận định nào sau đây là SAI?
- A Gia tốc có độ lớn tăng dần
- B Vận tốc và lực kéo về trái dấu
- C Tốc độ của vật giảm dần
- D Vật chuyển động chậm dần đều
Đáp án: D
Lời giải chi tiết:
Đáp án D
Câu hỏi 27 :
Một vật dao động điều hòa quanh vị trí cân bằng O với biên độ A và tần số f. Tốc độ trung bình của vật trong một chu kì được tính bằng biểu thức:
- A \(\overline v = 4f{\rm{A}}\)
- B \(\overline v = {{2{\rm{A}}} \over f}\)
- C \(\overline v = {{{\rm{4A}}} \over f}\)
- D \(\overline v = 2f{\rm{A}}\)
Đáp án: A
Phương pháp giải:
Sử dụng công thức tính tốc độ trung bình của vật trong một chu kì
Lời giải chi tiết:
\(\overline v = {{4A} \over T} = 4Af\)
Chọn A
Câu hỏi 28 :
Hai dao động điều hòa có phương trình lần lượt là \({x_1} = 5\cos (10\pi t + \frac{\pi }{2})\,cm,{x_2} = 3\cos (10\pi t - \frac{\pi }{6})cm\). Độ lệch pha của hai dao động này bằng
- A 2
- B 0
- C \(\frac{{2\pi }}{3}\)
- D \(\frac{\pi }{3}\)
Đáp án: C
Lời giải chi tiết:
Đáp án C
Câu hỏi 29 :
Một vật dao động điều hoà với biên độ 5cm. Quãng đường lớn nhất vật đi được trong 5/3 (s) là 35cm. Tại thời điểm vật kết thúc quãng đường 35cm đó thì tốc độ của vật là
- A \(5\pi \sqrt 3 cm/s\)
- B \(10\pi \sqrt 3 cm/s\)
- C \(\frac{{5\sqrt 3 }}{2}\pi (cm/s)\)
- D \(7\pi \sqrt 3 cm/s\)
Đáp án: A
Phương pháp giải:
Phương pháp: Sử dụng vòng tròn lượng giác và hệ thức độc lập theo thời gian của x và v
Lời giải chi tiết:
Đáp án A
Cách giải:
Quãng đường vật đi được: S = 35cm = 4A + 2A + A
Trong khoảng thời gian: ∆t = T + T/2 + ∆t’ = 5/3 s
Biểu diễn trên đường tròn lượng giác ta có:
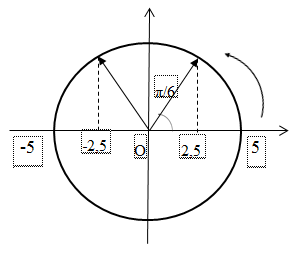
Khi vật đi từ vị trí có li độ 2,5 đến – 2,5 => góc quét được là α = π/6 + π/6 = π/3 thì vật đi được quãng đường A trong khoảng thời gian ∆t’ = (π/3).(T/2π) = T/6
=> ∆t = T + T/2 + T/6 = 5T/3 = 5/3 s => T = 1s => ω = 2π (rad/s)
Tại thời điểm kết thúc quãng đường 35cm, vật ở vị trí có li độ x = -2,5cm thì tốc độ của vật: \(v = \omega \sqrt {{A^2} - {x^2}} = 2\pi \sqrt {{5^2} - 2,{5^2}} = 5\pi \sqrt 3 cm/s\)
Câu hỏi 30 :
Một chất điểm dao động điều hoà với biên độ A = 5cm và chu kì T = 0,3s. Trong khoảng thời gian 0,1s, chất điểm không thể đi được quãng đường bằng
- A 9 cm
- B 8,0 cm
- C 7,5 cm
- D 8,5 cm
Đáp án: A
Phương pháp giải:
Phương pháp: Sử dụng vòng tròn lượng giác
Lời giải chi tiết:
Đáp án A
Cách giải:
Ta có: ∆t = 0,1s = T/3 => góc quét α = ω.∆t = 2π/3
Quãng đường lớn nhất vật đi được trong khoảng thời gian 0,1s được biểu diễn trên đường tròn lượng giác:
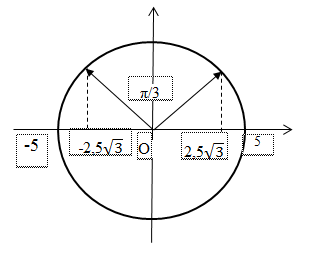
\( \Rightarrow {S_{m{\text{ax}}}} = 2.2,5\sqrt 3 = 5\sqrt 3 = 8,66cm\)
=> Trong 0,1s chất điểm không thể đi được quãng đường bằng 9cm
Câu hỏi 31 :
Một vật dao động điều hoà dọc theo một đường thẳng. Một điểm M nằm cố định trên đường thẳng đó, phía ngoài khoảng chuyển động của vật. Tại thời điểm t thì vật xa M nhất, sau đó một khoảng thời gian ngắn nhất là ∆t vật gần M nhất. Độ lớn vận tốc của vật bằng nửa tốc độ cực đại vào thời điểm gần nhất là
- A \(t + \frac{{2\Delta t}}{3}\)
- B \(t + \frac{{\Delta t}}{4}\)
- C \(t + \frac{{\Delta t}}{3}\)
- D \(t + \frac{{\Delta t}}{6}\)
Đáp án: D
Phương pháp giải:
Phương pháp: Sử dụng vòng tròn lượng giác
Lời giải chi tiết:
Đáp án D
Cách giải:
Tại thời điểm t vật xa M nhất => M ở biên âm
Tại thời điểm t + ∆t => M ở biên dương
=> ∆t = T/2 => T = 2∆t
Tại thời điểm t: vật ở vị trí biên thì vận tốc = 0
Tại thời điểm t + ∆t: độ lớn vận tốc của vật bằng nửa tốc độ cực. Biểu diễn trên đường tròn lượng giác của vận tốc ta có:
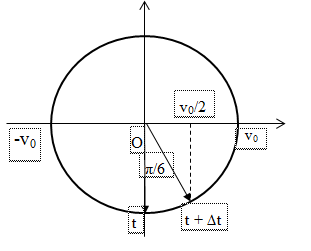
=> Góc quét α = π/6 => ∆t = (π/6).(T/2π) = T/12 = ∆t/6
=> Độ lớn vận tốc của vật bằng nửa tốc độ cực đại vào thời điểm: t + ∆t/6
Câu hỏi 32 :
Một vật dao động điều hòa với biên độ A, ban đầu vật đứng tại vị trí có li độ x = -5cm. Sau khoảng thời giản t1 vật về đến vị trí x = 5cm nhưng chưa đổi chiều chuyển động. Tiếp tục chuyển động thêm 18cm nữa vật về đến vị trí ban đầu và đủ một chu kì. Chiều dài quỹ đạo của vật có giá trị là:
- A 20 cm
- B 14 cm
- C 12 cm
- D 10 cm
Đáp án: B
Phương pháp giải:
Phương pháp: Chiều dài quỹ đạo của vật L = 2A
Lời giải chi tiết:
Đáp án B
Cách giải:
Quãng đường vật đi được trong 1 chu kì là: S = 5 + 5 + 18 = 28cm = 4A
=> A = 7cm
Chiều dài quỹ đạo của vật L = 2A = 14cm
=> Chọn B
Câu hỏi 33 :
Một vật dao động điều hoà với phương trình x = Acos(ωt + π/3) cm. Biết quãng đường vật đi được trong khoảng thời gian 1s là 2A và trong 2/3s là 9cm kể từ lúc bắt đầu dao động. Giá trị của A và ω là
- A 6cm và π rad/s
- B 12cm và π rad/s
- C 9cm và π rad/s
- D 12cm và 2π rad/s
Đáp án: A
Phương pháp giải:
Phương pháp: Sử dụng vòng tròn lượng giác
Lời giải chi tiết:
Đáp án A
Cách giải:
Quãng đường vật đi được trong T/2 là 2A => T/2 = 1 => T = 2s => ω = π (rad/s)
Trong ∆t = 2/3s => góc quét được là α = ω.∆t = 2π/3 (rad). Biểu diễn trên đường tròn lượng giác:
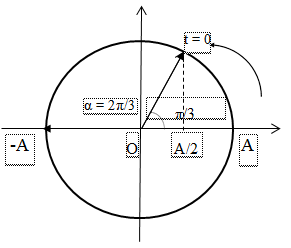
=> Quãng đường vật đi được trong 2/3s là: A/2 + A = 9cm => A = 6cm
Câu hỏi 34 :
Một chất điểm dao động điều hoà có vận tốc bằng 0 tại hai thời điểm liên tiếp là t1 = 2,2s và t2 = 2,9s. Tính từ thời điểm ban đầu (t0 = 0s) đến thời điểm t2 chất điểm đã đi qua vị trí cân bằng
- A 5 lần
- B 3 lần
- C 4 lần
- D 6 lần
Đáp án: C
Phương pháp giải:
Phương pháp:Sử dụng vòng tròn lượng giác
Lời giải chi tiết:
Đáp án C
Cách giải:
Khoảng thời gian giữa hai lần liên tiếp vận tốc bằng 0 là T/2 = 2,9 – 2,2 = 0,7s => T = 1,4s
2,9s = 2T + T/14
=> Góc quét được trong khoảng thời gian T/4 là: α = ω.T/14 = 5π/49
Xác định trên đường tròn lượng giác ta có:
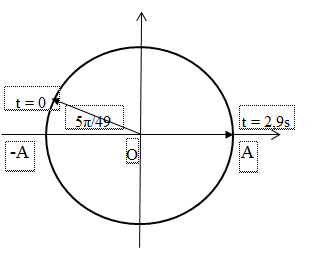
=> Tính từ thời điểm ban đầu đến thời điểm t2 = 2,9 s chất điểm đi qua VTCB 4 lần
Câu hỏi 35 :
Hai chất điểm M và N cùng xuất phát từ gốc O và bắt đầu dao động điều hòa cùng chiều dọc theo trục Ox với cùng biên độ nhưng với chu kì lần lượt là 3s và 6s. Tỉ số độ lớn vận tốc của điểm M và N khi chúng gặp nhau là:
- A 2:3
- B 1:2
- C 3:2
- D 2:1
Đáp án: D
Phương pháp giải:
Phương pháp: Sử dụng công thức về sự trùng phùng dao động
Lời giải chi tiết:
Đáp án D
Cách giải:
Hai con lắc gặp nhau khi \(t = \frac{{{T_1}{T_2}}}{{\left| {{T_1} - {T_2}} \right|}} = \frac{{3.6}}{3} = 6{\text{s}}\)
=> Chúng lại trở lại vị trí cb lúc đầu
=> tỉ số độ lớn vận tốc của điểm M và N lúc đó $\frac{{{v_M}}}{{{v_N}}} = \frac{{A{\omega _M}}}{{A{\omega _N}}} = \frac{{{\omega _M}}}{{{\omega _N}}} = \frac{{{T_N}}}{{{T_M}}} = \frac{6}{3} = 2$
=> Chọn D
Câu hỏi 36 :
Một vật dao động điều hoà với tần số góc ω = 10 rad/s. Khi vận tốc của vật là 20 cm/s thì gia tốc của vật bằng \(2\sqrt 3 m/{s^2}\). Biên độ dao động của vật là
- A 0,04cm
- B 2m
- C 2cm
- D 4cm
Đáp án: D
Phương pháp giải:
Phương pháp:Sử dụng hệ thức độc lập theo thời gian của v và a
Lời giải chi tiết:
Đáp án D
Cách giải:
Ta có: \(\frac{{{v^2}}}{{{\omega ^2}{A^2}}} + \frac{{{a^2}}}{{{\omega ^4}{A^2}}} = 1 \Rightarrow A = \sqrt {\frac{{{v^2}}}{{{\omega ^2}}} + \frac{{{a^2}}}{{{\omega ^4}}}} = \sqrt {\frac{{{{20}^2}}}{{{{10}^2}}} + \frac{{{{\left( {200\sqrt 3 } \right)}^2}}}{{{{10}^4}}}} = 4cm\)
Câu hỏi 37 :
Tốc độ và li độ của một chất điểm dao động điều hoà có hệ thức \(\frac{{{v^2}}}{{640}} + \frac{{{x^2}}}{{16}} = 1\), trong đó x tính bằng cm, v tính bằng cm/s. Tốc độ trung bình của chất điểm trong mỗi chu kì là
- A 0
- B 32 cm/s
- C 8 cm/s
- D 16 cm/s
Đáp án: D
Phương pháp giải:
Phương pháp : Áp dụng hệ thức độc lập trong dao động cơ \(\frac{{{v^2}}}{{{\omega ^2}{A^2}}} + \frac{{{x^2}}}{{{A^2}}} = 1\)
Lời giải chi tiết:
Đáp án D
Cách giải:
Từ điều kiện \(\frac{{{v^2}}}{{640}} + \frac{{{x^2}}}{{16}} = 1$$ ta có $$A = 4cm;\omega = \sqrt {40} \,\,rad/s = > T = \sqrt {0,1} \pi \,\,s\)
Vận tốc trung bình của chất điểm trong mỗi chu kỳ là \(\bar v = \frac{{4A}}{T} = \frac{{4.4}}{{\pi .\sqrt {0,1} }} = 16cm/s\)
Câu hỏi 38 :
Một chất điểm chuyển động tròn đều trên đường tròn tâm O với tốc độ dài là 30cm/s, có gia tốc hướng tâm là 1,5m/s2 thì hình chiếu của nó trên đường kính quỹ đạo dao động điều hoà với biên độ
- A 6cm
- B 4,5cm
- C 5cm
- D 7,5cm
Đáp án: A
Phương pháp giải:
Phương pháp: Sử dụng công thức tính tốc độ dài và gia tốc hướng tâm trong chuyển động tròn đều
Lời giải chi tiết:
Đáp án A
Cách giải:
Ta có:
\(\left\{ \matrix{
v = \omega r = 0,3(m/s) \hfill \cr
{a_{ht}} = {{{v^2}} \over r} = 1,5(m/{s^2}) \hfill \cr} \right. \Rightarrow {a_{ht}} = {{0,{3^2}} \over r} = 1,5 \Rightarrow r = {{0,{3^2}} \over {1,5}} = 6cm \Rightarrow A = r = 6cm\)
Câu hỏi 39 :
Một vật dao động điều hòa theo phương trình $x = 5c{\text{os}}\left( {\pi t + \frac{\pi }{4}} \right)cm$ . Kể từ t = 0, vật đi qua vị trí lực kéo về triệt tiêu lần thứ ba vào thời điểm:
- A 2,5 s
- B 2,75 s
- C 2,25 s
- D 2 s
Đáp án: C
Phương pháp giải:
Phương pháp: Sử dụng lí thuyết về dao động điều hoà
Lời giải chi tiết:
Đáp án C
Cách giải:
Chu kì: $T = \frac{{2\pi }}{\omega } = 2{\text{s}}$
Tại t = 0:
$\left\{ \matrix{
x = 5c{\rm{os}}{\pi \over 4} = 2,5\sqrt 2 \hfill \cr
v = - A\omega \sin {\pi \over 4} < 0 \hfill \cr} \right.$
Vị trí có lực kéo về triệt tiêu là: x = 0
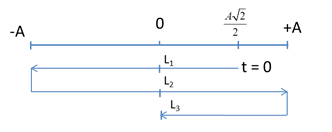
=> Thời gian kể từ t = 0, vật đi qua vị trí lực kéo về triệt tiêu lần thứ ba là: $t = \frac{T}{8} + \frac{{4T}}{4} = \frac{{9T}}{8} = 2,25{\text{s}}$
=> Chọn C
Câu hỏi 40 :
Một vật nhỏ dao động điều hòa trên trục Ox với vị trí cân bằng trùng gốc tọa độ O. Khi vật chuyển động nhanh dần theo chiều dương của trục Ox thì li độ x và vận tốc v của nó là
- A x > 0 và v < 0.
- B x < 0 và v < 0
- C x > 0 và v > 0
- D x < 0 và v > 0
Đáp án: D
Lời giải chi tiết:
Đáp án D