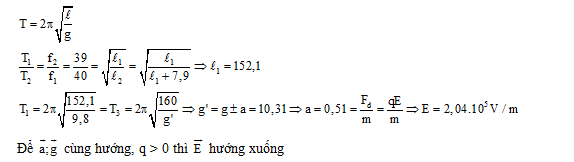Câu hỏi 1 :
Một con lắc đơn có chiều dài 1 m, đầu trên cố định đầu dưới gắn với vật nặng có khối lượng m. Điểm cố định cách mặt đất 2,5 m. Ở thời điểm ban đầu đưa con lắc lệch khỏi vị trí cân bằng một góc a = 0,09 rad, rồi thả nhẹ khi con lắc vừa qua vị trí cân bằng thì sợi dây bị đứt. Bỏ qua mọi sức cản, lấy g = 9,8 m/s2. Tốc độ của vật nặng ở thời điểm t = 0,08 s có giá trị gần bằng:
- A 0,35 m/s.
- B 0,83 m/s.
- C 0,57 m/s.
- D 0,069 m/s.
Đáp án: D
Phương pháp giải:
Áp dụng công thức \(v = \sqrt {2gl(c{\rm{os}}\alpha - c{\rm{os}}{\alpha _0})} \)
Lời giải chi tiết:
Đáp án D
Chu kỳ dao động của con lắc: \(T = 2\pi \sqrt {{\ell \over g}} \) = 2s => ω = π rad/s
Thời điểm sợi dây treo con lắc bị đứt là t0 = T/4 = 0,5s
Vậy thời điểm t = 0,08s con lắc chưa bị đứt.
PT dao động của con lắc: \(\alpha = {\alpha _0}cos\pi t\)
Khi t = 0,08s thì α = 0,087 rad
Tốc độ của vật nặng khi đó: \(v = \sqrt {2.9,8.1.(c{\rm{os 0}}{\rm{,0872 - cos 0}}{\rm{,09}})} = 0,069m/s\)
Câu hỏi 2 :
Một con lắc đơn gồm một vật nhỏ khối lượng m = 2g và một dây treo mảnh, chiều dài l, được kích thích cho dao động điều hòa, Trong khoảng thời gian Δt con lắc thực hiện được 40 dao động. Khi tăng chiều dài con lắc thêm một đoạn 7,9cm thì cũng trong khoảng thời gian Δt con lắc thực hiện được 39 dao động. Lấy gia tốc trọng trường g = 9,8m/s2. Để con lắc với chiều dài tăng thêm có cùng chu kỳ dao động với con lắc chiều dài l, người ta truyền cho vật điện tích q = + 0,5.10-8C rồi cho nó dao động điều hòa trong một điện trường đều có đường sức thẳng đứng. Vecto cường độ điện trường này có
- A chiều hướng lên và độ lớn 1,02.105V/m
- B chiều hướng xuống và độ lớn bằng 1,02.105V/m
- C chiều hướng lên và độ lớn 2,04.105V/m
- D Chiều hướng xuống và độ lớn 2,04.105V/m
Đáp án: D
Lời giải chi tiết:
Câu hỏi 3 :
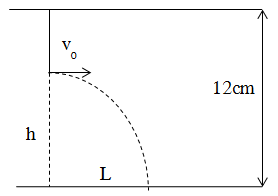
Một con lắc đơn có chiều dài l được treo dưới gầm cầu cách mặt nước 12 m. Con lắc đơn dao động điều hòa với biên độ góc α0 = 0,1 rad. Khi vật đi qua vị tri cân bằng thì dây bị đứt. Khoảng cách cực đại ( tính theo phương ngang) từ điểm treo con lắc đến điểm mà vật nặng rơi trên mặt nước mà con lắc thể đạt được là.
- A 75 cm.
- B 95 cm.
- C 65 cm.
- D 85 cm.
Đáp án: D
Phương pháp giải:
Sử dụng lí thuyết về dao động điều hòa của con lắc đơn kết hợp với chuyển động ném ngang
Lời giải chi tiết:
Gọi khoảng cách từ VTCB của con lắc đến mặt nước là h
=> dây treo con lắc có chiều dài l = 12 – h
Vận tốc của con lắc khi đi qua VTCB: \({v_0} = {v_{\max }} = \sqrt {gl\alpha _0^2} = \sqrt {g(12 - h)\alpha _0^2} \)
Tại đây, dây treo con lắc bị đứt => con lắc sẽ chuyển động như một vật bị ném ngang với vận tốc ban đầu v0
=> Tầm bay xa : \(L = {v_0}\sqrt {\frac{{2h}}{g}} = \sqrt {2(12 - h)h\alpha _0^2} = {\alpha _0}\sqrt 2 .\sqrt {(12 - h).h} \)
Nhận xét: \(\sqrt {(12 - h).h} \le \frac{{12 - h + h}}{2} = 6\)(theo Cô-si) =>\(L \le 6\sqrt 2 {\alpha _0} \approx 0,85m = 85cm\)
Vậy Lmax = 85cm => Chọn D
Câu hỏi 4 :
Một con lắc đơn gồm sợi dây mảnh dài l=1m, vật có khối lượng m=100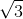 g tích điện q=10-5 (C). Treo con lắc đơn trong điện trường đều có phương vuông góc với gia tốc trọng trường và có độ lớn E=105 V/m. Kéo vật theo chiều của vec tơ điện trường sao cho góc tạo bởi dây treo và bằng 600 rồi thả nhẹ để vật dao động. Lực căng cực đại của dây treo là
g tích điện q=10-5 (C). Treo con lắc đơn trong điện trường đều có phương vuông góc với gia tốc trọng trường và có độ lớn E=105 V/m. Kéo vật theo chiều của vec tơ điện trường sao cho góc tạo bởi dây treo và bằng 600 rồi thả nhẹ để vật dao động. Lực căng cực đại của dây treo là
- A 3,54 N.
- B 2,14 N.
- C 2,54 N.
- D 1,54 N.
Đáp án: C
Lời giải chi tiết:
Câu hỏi 5 :
Một con lắc đơn gồm một vật nhỏ có khối lượng m=2 g và một dây treo mảnh, chiều dài l, được kích thích cho dao động điều hòa. Trong khoảng thời gian Δt con lắc thực hiện được 40 dao động. Khi tăng chiều dài con lắc thêm một đoạn bằng 7,9cm, thì cũng trong khoảng thời gian Δt con lắc thực hiện được 39 dao động. Lấy gia tốc trọng trường g=9,8 m/s2. Để con lắc với chiều dài tăng thêm có cùng chu kỳ dao động với con lắc có chiều dài l, người ta truyền cho vật điện tích q=-10-8 C rồi cho nó dao động điều hòa trong một điện trường đều có đường sức thẳng đứng. Véc tơ cường độ điện trường này có
- A chiều hướng lên và độ lớn bằng 2,04.105 V/m.
- B chiều hướng lên và độ lớn bằng 1,02.105 V/m.
- C chiều hướng xuống và độ lớn bằng 2,04.105 V/m.
- D chiều hướng xuống và độ lớn bằng 1,02.105 V/m.
Đáp án: B
Lời giải chi tiết:
Câu hỏi 6 :
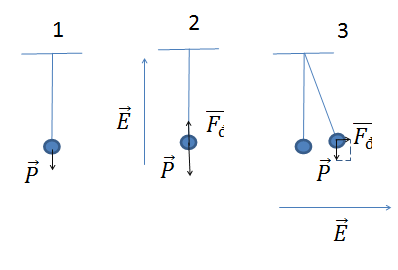
Con lắc đơn gồm quả cầu nhỏ tích điện q và sợi dây không co giãn, không dẫn điện. Khi chưa có điện trường con lắc dao động điều hòa với chu kì 2 s. Sau đó treo con lắc vào điện trường đều, có phương thẳng đứng thì con lắc dao động điều hòa với chu kì 4 s. Khi treo con lắc trong điện trường có cường độ điện trường như trên và có phương ngang thì chu kì dao động điều hòa của con lắc bằng:
- A 2,15 s.
- B 1,87 s.
- C 0,58 s.
- D 1,79 s.
Đáp án: D
Phương pháp giải:
Vận dụng bài toán con lắc chịu tác dụng của lực điện.
Lời giải chi tiết:
Đáp án D
$$P = mg,{\rm{ }}{F_d} = qE$$
Biểu diễn lực như hình, ta có:
Khi chưa có điện trường: ${T_1} = 2\pi \sqrt {{l \over g}} $
Khi điện trường có phương thẳng đứng: $${T_2} = 2\pi \sqrt {{l \over {g'}}} $$
trong đó: $$g' = \left| {g - {{qE} \over m}} \right|$$
Khi điện trường có phương ngang: $${T_3} = 2\pi \sqrt {{l \over {g}}} $$
trong đó: $$g = \sqrt {{g^2} + {{({{qE} \over m})}^2}} $$
Ta có: $${{{T_1}} \over {{T_2}}} = \sqrt {{{g'} \over g}} \to {{\left| {g - {{qE} \over m}} \right|} \over g} = {({{{T_1}} \over {{T_2}}})^2} = {1 \over 4} \to 4(g - {{qE} \over m}) = g \to {{qE} \over m} = {3 \over 4}g$$
$${{{T_1}} \over {{T_3}}} = \sqrt {{{g} \over g}} \to \sqrt {{{\sqrt {{g^2} + {{({{qE} \over m})}^2}} } \over g}} = \sqrt {{5 \over 4}} \to {T_3} = {T_1}{2 \over {\sqrt 5 }} = 1,79{\rm{s}}$$
Câu hỏi 7 :
Hai con lắc đơn có cùng chiều dài dây treo, cùng khối lượng vật nặng m = 10g. Con lắc thứ nhất mang điện tích q, con lắc thứ hai không tích điện. Đặt cả hai con lắc vào điện trường đều, thẳng đứng lên trên, cường độ E = 11.104 V/m. Trong cùng một khoảng thời gian, nếu con lắc thứ nhất thực hiện 6 dao động thì con lắc thứ hai thực hiện 5 dao động. Tính q. Cho g = 10m/s2. Bỏ qua sức cản của không khí.
- A – 4.10-7 C
- B 4.10-6 C
- C 4.10-7 C
- D – 4.10-6 C
Đáp án: A
Phương pháp giải:
Sử dụng lí thuyết con lắc đơn chịu thêm tác dụng của lực điện
Lực điện : \(\overrightarrow {{F_d}} = q\overrightarrow E \)
Chu kì : T = ∆t/N (N là số dao động toàn phần thực hiện được trong thời gian ∆t)
Lời giải chi tiết:
Ta có :
\(\left\{ \matrix{ {T_1} = 2\pi \sqrt {{l \over {g'}}} = {{\Delta t} \over 6} \hfill \cr {T_2} = 2\pi \sqrt {{l \over g}} = {{\Delta t} \over 5} \hfill \cr} \right. \Rightarrow {T_1} < {T_2} \Rightarrow g' > g \Rightarrow g' = g + {{\left| q \right|E} \over m} \Rightarrow \overrightarrow P \uparrow \uparrow \overrightarrow {{F_d}} \Rightarrow q < 0\)
\( \Rightarrow {{{T_1}} \over {{T_2}}} = \sqrt {{g \over {g'}}} = {5 \over 6} \Leftrightarrow {g \over {g + {{\left| q \right|E} \over m}}} = {{25} \over {36}} \Rightarrow \left| q \right| = {{11.g.m} \over {25E}} = {{{{11.10.10.10}^{ - 3}}} \over {{{25.11.10}^4}}} = {4.10^{ - 7}} \Rightarrow q = - {4.10^{ - 7}}C\)
Chọn A
Câu hỏi 8 :
Một con lắc đơn có chiều dài dây treo 50cm và vật nhỏ có khối lượng 0,01 kg mang điện tích q = +5.10-6C, được coi là điện tích điểm. Con lắc dao động điều hòa trong điện trường đều mà vecto cường độ điện trường có độ lớn E = 104 V/m và hướng thẳng đứng xuống dưới. Lấy g = 10 (m/s2), π = 3,14. Chu kì dao động điều hòa của con lắc là
- A 1,15s.
- B 1,99s.
- C 0,58s.
- D 1,40s
Đáp án: A
Phương pháp giải:
Sử dụng công thức tính chu kỳ với gia tốc biểu kiến
Lời giải chi tiết:
Vì E hướng xuống dưới và điện tích dương nên lực điện tác dụng vào quả nặng cũng hướng xuống dưới, cùng chiều với trọng lực.
Áp dụng công thức
\(T = 2\pi .\sqrt {\frac{l}{{g + \frac{{q.E}}{m}}}} = 2\pi .\sqrt {\frac{{0,5}}{{10 + \frac{{{{5.10}^{ - 6}}{{.10}^4}}}{{0,01}}}}} = 1,15s\)
Câu hỏi 9 :
Tại nơi có gia tốc trọng trường g = 10 m/s2, một con lắc đơn có chiều dài 1 m, dao động với biên độ góc 600. Trong quá trình dao động, cơ năng của con lắc được bảo toàn. Tại vị trí dây treo hợp với phương thẳng đứng góc 300, gia tốc của vật nặng của con lắc có độ lớn là
- A 732 cm/s2
- B 500 cm/s2.
- C 887 cm/s2.
- D 1232 cm/s2.
Đáp án: C
Phương pháp giải:
- Con lắc dao động với góc lớn hơn 100 không phải là dao động điều hòa
- Vận tốc của con lắc đơn: \(v=\sqrt{2g\ell (c\text{os}\alpha \text{-cos}{{\alpha }_{0}})}\)
- Gia tốc của con lắc chia là hai thành phần tiếp tuyến và pháp tuyến.
at = gsinα ; an = v2/l
- Gia tốc của vật là: \(a=\sqrt{a_{n}^{2}+a_{t}^{2}}\)
Lời giải chi tiết:
+ Các gia tốc thành phần của con lắc:
\({{a}_{t}}=g\,\sin \,\alpha =5\,m/{{s}^{2}},\,{{a}_{n}}=\frac{{{v}^{2}}}{1}=2g\left( \cos \,\alpha -\cos {{\alpha }_{0}} \right)=7,32\,m/{{s}^{2}}\)
\(\Rightarrow \) Gia tốc của vật \(a=\sqrt{a_{n}^{2}+a_{t}^{2}}=887\,cm/{{s}^{2}}\)
Câu hỏi 10 :
Một con lắc đơn có chiều dài l được treo dưới gầm cầu cách mặt nước 12 m. Con lắc đơn dao động điều hòa với biên độ góc α0 = 0,1 rad. Khi vật đi qua vị tri cân bằng thì dây bị đứt. Khoảng cách cực đại ( tính theo phương ngang) từ điểm treo con lắc đến điểm mà vật nặng rơi trên mặt nước mà con lắc thể đạt được là.
- A 75 cm.
- B 95 cm.
- C 65 cm.
- D 85 cm.
Đáp án: D
Phương pháp giải:
Phương pháp:
Sử dụng lí thuyết về dao động điều hòa của con lắc đơn kết hợp với chuyển động ném ngang
Lời giải chi tiết:
Cách giải:
Gọi khoảng cách từ VTCB của con lắc đến mặt nước là h
=> dây treo con lắc có chiều dài l = 12 – h
Vận tốc của con lắc khi đi qua VTCB: \({v_0} = {v_{\max }} = \sqrt {gl\alpha _0^2} {\rm{\;}} = \sqrt {g(12 - h)\alpha _0^2} \)
Tại đây, dây treo con lắc bị đứt => con lắc sẽ chuyển động như một vật bị ném ngang với vận tốc ban đầu v0
=> Tầm bay xa : \(L = {v_0}\sqrt {\frac{{2h}}{g}} {\rm{\;}} = \sqrt {2(12 - h)h\alpha _0^2} {\rm{\;}} = {\alpha _0}\sqrt 2 .\sqrt {(12 - h).h} \)
Nhận xét: \(\sqrt {(12 - h).h} {\rm{\;}} \le \frac{{12 - h + h}}{2} = 6\)(theo Cô-si) =>\(L \le 6\sqrt 2 {\alpha _0} \approx 0,85m = 85cm\)
Vậy Lmax = 85cm
Chọn D
Câu hỏi 11 :
Một con lắc đơn gồm sợi dây mảnh dài l=1m, vật có khối lượng \(m = 100\;\sqrt 3 g\)tích điện q=10-5 (C). Treo con lắc đơn trong điện trường đều có phương vuông góc với gia tốc trọng trường và có độ lớn E=105V/m. Kéo vật theo chiều của vec tơ điện trường sao cho góc tạo bởi dây treo và bằng 600 rồi thả nhẹ để vật dao động. Lực căng cực đại của dây treo là
- A 3,54 N.
- B 2,14 N.
- C 2,54 N.
- D 1,54 N.
Đáp án: C
Phương pháp giải:
Phương pháp giải: Sử dụng lí thuyết về con lắc đơn chịu tác dụng của ngoại lực
Lời giải chi tiết:
Cách giải:
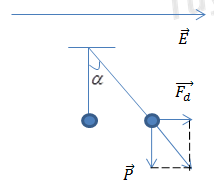
VTCB mới của con lắc là VT mà dây treo hợp với phương thẳng đứng góc β sao cho
\(\tan \beta = \frac{{\left| q \right|E}}{{mg}} = \frac{{{{10}^{ - 5}}.10{}^5}}{{100\sqrt 3 {{.10}^{ - 3}}.10}} = \frac{1}{{\sqrt 3 }} = > \beta = {30^{^0}}(rad)\)
Kéo con lắc đơn ra khỏi phương thẳng đứng góc 600 rồi thả nhẹ => CLĐ sẽ dao động với biên độ α0 = 300.
Gia tốc trọng trường hiệu dụng \({g'} = \sqrt {{g2} + {a^2}} = \sqrt {{g^2} + {g^2}{{\tan }^2}\beta } = \frac{{2g}}{{\sqrt 3 }}\)
Lực căng dây cực đại của con lắc đơn: \({T_{\max }} = mg'(3 - 2\cos {\alpha _0}) = 100\sqrt 3 {.10^{ - 3}}.\frac{{2.10}}{{\sqrt 3 }}(3 - 2cos{30^0}) = 2,54(N)\)
Chọn C
Câu hỏi 12 :
Một con lắc đơn gồm một vật nhỏ có khối lượng m=2 g và một dây treo mảnh, chiều dài l, được kích thích cho dao động điều hòa. Trong khoảng thời gian Δt con lắc thực hiện được 40 dao động. Khi tăng chiều dài con lắc thêm một đoạn bằng 7,9cm, thì cũng trong khoảng thời gian Δt con lắc thực hiện được 39 dao động. Lấy gia tốc trọng trường g=9,8 m/s2. Để con lắc với chiều dài tăng thêm có cùng chu kỳ dao động với con lắc có chiều dài l, người ta truyền cho vật điện tích q=-10-8 C rồi cho nó dao động điều hòa trong một điện trường đều có đường sức thẳng đứng. Véc tơ cường độ điện trường này có
- A chiều hướng lên và độ lớn bằng 2,04.105 V/m.
- B chiều hướng lên và độ lớn bằng 1,02.105 V/m.
- C chiều hướng xuống và độ lớn bằng 2,04.105 V/m.
- D chiều hướng xuống và độ lớn bằng 1,02.105 V/m.
Đáp án: B
Phương pháp giải:
Phương pháp:
+ Sử dụng công thức tính chu kì của con lắc đơn \(T = 2\pi \sqrt {\frac{l}{g}} \)
+ Sử dụng thuyết về con lắc chịu tác dụng của lực điện trường.
Lời giải chi tiết:
Cách giải :
Cụ thể:
+ Chiều dài của con lắc là l.
Khi chiều dài là l→ chu kì dao động \(T = \frac{{\Delta t}}{{40}}\)
Khi chiều dài là l+7,9cm→ chu kì dao động \(T' = \frac{{\Delta t}}{{39}}\)
=> \(\frac{l}{{l + 7,9}} = \frac{{{T^2}}}{{T{'^2}}} = \frac{{{{39}^2}}}{{{{40}^2}}}\) => l=152,1 cm.
+ Con lắc có chiều dài tăng thêm là l’=l+7,9 cm=160 cm, tích thêm điện tích q= -10-8C
Theo đề bài: T’=T có \(\sqrt {\frac{{{l'}}}{{{g'}}}} = \sqrt {\frac{l}{g}} \)=> g’=g. \(\frac{{{l'}}}{g} = 9,8.\frac{{160}}{{152,1}} = 10,31\) m/s2.
NX: g’>g mà \(\overrightarrow {g'} = \overrightarrow g + \frac{{\overrightarrow F }}{m}\)=> \(\overrightarrow F \uparrow \uparrow \overrightarrow g \) mà q\(\overrightarrow E \uparrow \downarrow \overrightarrow g \) hay \(\overrightarrow E \) thẳng đứng hướng lên.
Và, \(\frac{{\left| q \right|E}}{m} = g' - g = > E = \frac{{(g' - g).m}}{{\left| q \right|}} = \frac{{(10,31 - 9,8){{.2.10}^{ - 3}}}}{{{{10}^{ - 8}}}} = 10200V/m = 1,{02.10^5}V/m.\)
Chọn B.
Câu hỏi 13 :
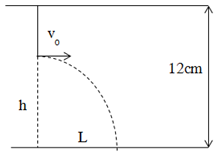
Con lắc đơn trong phòng thí nghiệm có \(T = 2{\rm{ }}s\) được treo vào trần một ô tô. Cho \(g = {\pi ^{2\,\,}}m/{s^2}\). Biết ôtô lên dốc nhanh dần đều với gia tốc \(a = \sqrt 3 g\) . Biết dốc nghiêng một góc \(\beta = {30^0}\) so với phương ngang. Hãy xác định vị trí cân bằng của con lắc và chu kì dao động nhỏ của nó ?
- A \(2,91{\rm{ }}s{\rm{ }};{\rm{ }}{38^0}50'\)
- B \(3,25{\rm{ }}s{\rm{ }};{\rm{ }}{48^0}50'\)
- C \(1,29{\rm{ }}s{\rm{ }};{\rm{ }}{38^0}50'\)
- D \(1,29{\rm{ }}s{\rm{ }};{\rm{ }}{48^0}50'\)
Đáp án: C
Phương pháp giải:
+ Áp dụng công thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \)
+ Áp dụng bài toán con lắc đơn chịu thêm tác dụng của lực quán tính: \(\overrightarrow {{F_{qt}}} = - m\overrightarrow a \)
Lời giải chi tiết:
Ta có:
+ Chu kì dao động của con lắc đơn khi ở trong phòng thí nghiệm: \(T = 2\pi \sqrt {\frac{l}{g}} \)
+ Oto lên nhanh dần trên dốc nghiêng (\(\overrightarrow a \) xiên lên) \( \to \overrightarrow {{F_{qt}}} \) xiên xuống
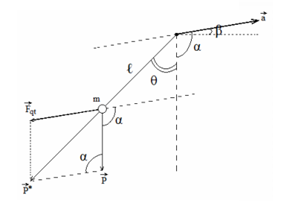
Ta có:
\(\begin{array}{l}P' = \sqrt {{P^2} + F_{qt}^2 - 2P{F_{qt}}{\rm{cos(90 + }}\beta {\rm{)}}} \\ \Rightarrow g' = \sqrt {{g^2} + {a^2} - 2g.a.c{\rm{os(90 + }}\beta {\rm{)}}} = \sqrt {{g^2} + {a^2} - 2g.a.c{\rm{os(90 + 3}}{{\rm{0}}^0}{\rm{)}}} = 2,394g\end{array}\)
\(\frac{{T'}}{T} = \sqrt {\frac{g}{{g'}}} = \sqrt {\frac{g}{{2,394g}}} = 0,646 \Rightarrow T' = 0,646.2 = 1,293{\rm{s}}\)
Khi nằm cân bằng con lắc hợp với phương thẳng đứng góc θ
Ta có: \(\frac{a}{{\sin \theta }} = \frac{{g'}}{{\sin ({{90}^0} + \beta )}} \Rightarrow \sin \theta = \frac{{a\sin ({{90}^0} + \beta )}}{{g'}} = \frac{{\sqrt 3 g.\sin ({{90}^0} + 30)}}{{2,394g}} = 0,627 \Rightarrow \theta = {38^0}49'44\)
Chọn C
Câu hỏi 14 :
Con lắc đơn gồm một hòn bi có khối lượng m treo trên sợi dây dài ℓ = 1 m ở tại nơi có gia tốc trọng trường g = 9,8 m/s2. Bỏ qua mọi ma sát và lực cản môi trường. Con lắc trên được treo vào trần một ôtô chuyển động nhanh dần điều với gia tốc a = 2 m/s2 từ đỉnh mặt phẳng nghiêng với mặt phẳng ngang một góc 300. Hỏi con lắc dao động với chu kì bằng bao nhiêu ?
- A 3,569 s.
- B 1,898 s.
- C 3,028 s.
- D 2,098 s.
Đáp án: D
Phương pháp giải:
+ Áp dụng công thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \)
+ Áp dụng bài toán con lắc đơn chịu thêm tác dụng của lực quán tính: \(\overrightarrow {{F_{qt}}} = - m\overrightarrow a \)
Lời giải chi tiết:
Ta có:
+ Oto lên nhanh dần xuống dốc nghiêng (\(\overrightarrow a \) xiên xuống) \( \to \overrightarrow {{F_{qt}}} \) xiên lên
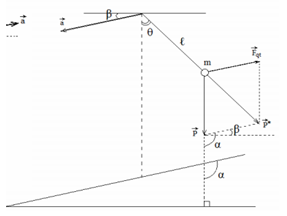
Ta có: \(P' = \sqrt {{P^2} + F_{qt}^2 - 2P{F_{qt}}{\rm{cos(90 - }}\beta {\rm{)}}} \)
\(\begin{array}{l} \Rightarrow g' = \sqrt {{g^2} + {a^2} - 2g.a.\cos {\rm{(90 - }}\beta {\rm{)}}} = \sqrt {{g^2} + {a^2} - 2g.a.\cos {\rm{(90 - 3}}{{\rm{0}}^0}{\rm{)}}} = 8,969m/{s^2}\\ \Rightarrow T' = 2\pi \sqrt {\frac{{\mathop{\rm l}\nolimits} }{{g'}}} = 2\pi \sqrt {\frac{1}{{8,969}}} = 2,098{\rm{s}}\end{array}\)
Chọn D
Câu hỏi 15 :
Một con lắc đơn gồm quả cầu nhỏ có khối lượng m = 200(g) treo vào sợi dây có chiều dài l = 1(m) dao động điều hòa, tại vị trí dây treo có góc lệch \(\alpha = 5{\sqrt 3 ^0}\) thì có tốc độ bằng một nửa tốc độ cực đại. Cho g = 10(m/s2), cơ năng của con lắc có giá trị là: (Cho π = 3,14)
- A 0,02(J)
- B 0,04(J)
- C 0,05(J)
- D 0,03(J)
Đáp án: D
Phương pháp giải:
Cơ năng: \({\rm{W}} = mgl\left( {1 - \cos \alpha } \right) + \frac{1}{2}m.{v^2} = mgl\left( {1 - \cos {\alpha _0}} \right) = \frac{1}{2}.m.v_0^2\)
Lời giải chi tiết:
Khi \(v = \frac{1}{2}{v_0}\) thì
\(\begin{array}{l}
{\rm{W}} = mgl\left( {1 - \cos {{\left( {5\sqrt 3 } \right)}^0}} \right) + \frac{1}{2}m.\frac{{v_0^2}}{4} = \frac{1}{2}.m.v_0^2\\
\Rightarrow {{\rm{W}}_t} = \frac{3}{4}{\rm{W}} \Rightarrow mgl\left( {1 - \cos {{\left( {5\sqrt 3 } \right)}^0}} \right) = \frac{3}{4}.mgl\left( {1 - \cos {\alpha _0}} \right)\\
\Leftrightarrow {\rm{W}} = \frac{{mgl\left( {1 - \cos {{\left( {5\sqrt 3 } \right)}^0}} \right)}}{{\frac{3}{4}}} = 0,03J
\end{array}\)
Chọn D
Câu hỏi 16 :
Hai con lắc đơn giống hệt nhau mà các vật nhỏ mang điện tích như nhau, được treo ở một nơi trên mặt đất. Trong mỗi vùng không gian chứa mỗi con lắc có một điện trường đều. Hai điện trường này có cùng cường độ nhưng các đường sức vuông góc với nhau. Giữ hai con lắc ở vị trí các dây treo có phương thẳng đứng rồi thả nhẹ thì chúng dao động điều hòa trong cùng một mặt phẳng với biên độ góc 80 và có chu kì tương ứng là T1 và T2 = T1 + 0,3s. Giá trị của T2 là
- A 1,645 s.
- B 1,974 s.
- C 2,274 s.
- D 1,895 s.
Đáp án: C
Phương pháp giải:
Chu kì của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{l}{g}} \)
Lực điện: \(\overrightarrow {{F_d}} = q.\overrightarrow E \)
Định lí hàm số sin trong tam giác: \(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}}\)
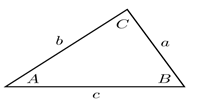
Lời giải chi tiết:
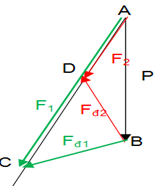
Trong hình vẽ, Fđ1 và Fđ2 là lực điện trong 2 trường hợp, F1 và F2 là hợp lực của trọng lực và lực điện trong 2 trường hợp, g1’ và g2’ là gia tốc biểu kiến trong 2 trường hợp.
Do lực điện trong 2 trường hợp có độ lớn bằng nhau và chiều vuông góc với nhau nên \(\Delta BCD\)vuông cân tại B.
Biên độ trong hai trường hợp đều bằng 80 \( \Rightarrow \widehat {BAC} = {8^0}\)
\(\begin{array}{l}\widehat {ABC} = {180^0} - \widehat C - \widehat A = {180^0} - {45^0} - {8^0} = {127^0}\\ \Rightarrow \widehat {ABD} = \widehat {ABC} - \widehat {DBC} = {127^0} - {90^0} = {37^0}\end{array}\)
Xét tam giác ABD: \(\dfrac{{{F_2}}}{{\sin {{37}^0}}} = \dfrac{{{F_{d2}}}}{{\sin {8^0}}}\,\,\,\,\,\left( 1 \right)\)
Xét tam giác ABC: \(\dfrac{{{F_1}}}{{\sin {{127}^0}}} = \dfrac{{{F_{d1}}}}{{\sin {8^0}}}\,\,\,\,\left( 2 \right)\)
Mà
\(\begin{array}{l}\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{{T_1}}}{{{T_1} + 0,{3_1}}} = \sqrt {\dfrac{{{g_2}'}}{{{g_1}'}}} = \sqrt {0,753554} = 0,868\\ \Rightarrow {T_1} = 1,973s \Rightarrow {T_2} = {T_1} + 0,3 = 2,273s\end{array}\)
Chọn C
Câu hỏi 17 :
Hai con lắc đơn giống hệt nhau mà các vật nhỏ mang điện tích như nhau, được treo ở một nơi trên mặt đất. Trong mỗi vùng không gian chứa mỗi con lắc có một điện trường đều. Hai điện trường này có cùng cường độ nhưng các đường sức vuông góc với nhau. Giữ hai con lắc ở vị trí các dây treo có phương thẳng đứng rồi thả nhẹ thì chúng giao động điều hòa trong cùng một mặt phẳng với biên độ góc 8o và có chu kí tương ứng là \({{T}_{1}}\) và \({{T}_{2}}={{T}_{1}}+0,3\left( s \right)\). Giá trị của T1 là
- A
2,247 s.
- B
1,645 s.
- C
1,895 s.
- D
1,974 s.
Đáp án: D
Phương pháp giải:
Khi giữ hai con lắc ở vị trí các dây treo có phương thẳng đứng rồi thả nhẹ thì chúng dao động điều hòa có 1 biên ở vị trí dây có phương thẳng đứng. Hai con lắc dao động với cùng biên độ góc là 8o nên gia tốc trọng trường hiệu dụng được biểu diễn như hình vẽ. (với \(\overrightarrow{{{a}_{1}}}\bot \overrightarrow{{{a}_{2}}}\), là gia tốc do lực điện trường gây ra).
\(\overrightarrow{{{g}_{1}}}=\overrightarrow{g}+\overrightarrow{{{a}_{1}}}\); \(\overrightarrow{{{g}_{2}}}=\overrightarrow{g}+\overrightarrow{{{a}_{2}}}\)
Áp dụng định lí hàm số sin và công thức: \(\frac{{{T}_{1}}}{{{T}_{2}}}=\sqrt{\frac{{{g}_{2}}}{{{g}_{1}}}}\)
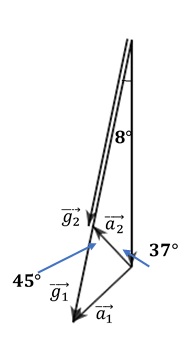
Lời giải chi tiết:
Ta có: \(\overrightarrow{{{g}_{1}}}=\overrightarrow{g}+\overrightarrow{{{a}_{1}}}\); \(\overrightarrow{{{g}_{2}}}=\overrightarrow{g}+\overrightarrow{{{a}_{2}}}\)
Hai vật có cùng điện tích đặt trong điện trường có cùng cường độ nhưng đường sức vuông góc nên lực điện tác dụng lên 2 vật bằng nhau \(\Rightarrow {{a}_{1}}={{a}_{2}}\)
Áp dụng định lí hàm số sin: \(\frac{{{g}_{1}}}{\sin {{127}^{o}}}=\frac{{{a}_{1}}}{\sin {{8}^{o}}}=\frac{{{a}_{2}}}{\sin {{8}^{o}}}=\frac{{{g}_{2}}}{\sin {{37}^{o}}}\)
\(\Rightarrow \frac{{{g}_{1}}}{{{g}_{2}}}=\frac{\sin {{127}^{o}}}{\sin {{37}^{o}}}\Rightarrow \frac{{{T}_{2}}}{{{T}_{1}}}=\sqrt{\frac{{{g}_{1}}}{{{g}_{2}}}}=\sqrt{\frac{\sin {{127}^{o}}}{\sin {{37}^{o}}}}\)\(\Rightarrow \frac{{{T}_{1}}+0,3}{{{T}_{1}}}=\sqrt{\frac{\sin {{127}^{o}}}{\sin {{37}^{o}}}}\Rightarrow {{T}_{1}}=1,974\left( s \right)\)
Chọn D
Câu hỏi 18 :
Một sợi dây nhẹ, không dãn, dài 100 cm được buộc chặt vào hai điểm cố định A và B trên một đường thẳng nằm ngang cách nhau 60 cm. Một hạt cườm nhỏ, nặng, được xâu vào dây và có thể trượt không ma sát dọc theo dây. Ban đầu hạt cườm đứng yên tại vị trí cân bằng. Kéo hạt cườm lệch khỏi vị trí cân bằng một đoạn nhỏ rồi buông nhẹ cho nó dao động điều hòa trong mặt phẳng vuông góc với AB và bỏ qua sức cản của không khí. Hạt cườm dao động với tần số góc có giá trị gần giá trị nào sau đây nhất?
- A \(2\pi \,\,rad/s\)
- B 2 rad/s
- C 5 rad/s
- D \(4\pi \,\,rad/s\)
Đáp án: C
Phương pháp giải:
Tần số góc của dao động: \(\omega =\sqrt{\frac{g}{l}}\)
Lời giải chi tiết:
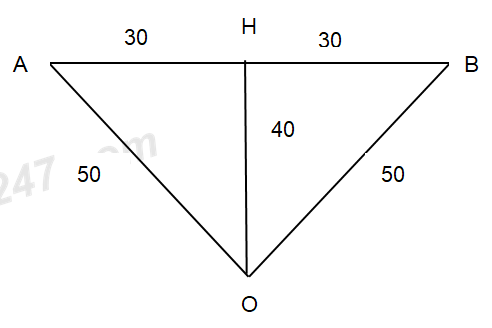
Ta có AB = 60 cm → AH = HB = 30 cm
Chiều dài dây l = 100 cm → AO = OB = 50 cm
→ OH = 40 cm
Coi dao động của hạt cườm là dao động của con lắc đơn có chiều dài 40 cm.
Tần số góc của hạt cườm là:
\(\omega =\sqrt{\frac{g}{l}}=\sqrt{\frac{10}{0,4}}=5\,\,\left( rad \right)\)
Chọn C.
Câu hỏi 19 :
Một con lắc đơn đang dao động điều hòa với biên độ góc \({{5}^{0}}\). Khi vật nặng đi qua vị trí cân bằng thì người ta giữ chặt điểm chính giữa của dây treo, sau đó vật tiếp tục dao động điều hòa với biên độ góc \({{\alpha }_{0}}\). Giá trị của \({{\alpha }_{0}}\) bằng
- A \(7,{{1}^{0}}\)
- B \({{10}^{0}}\)
- C \(3,{{5}^{0}}\)
- D \(2,{{5}^{0}}\)
Đáp án: A
Phương pháp giải:
Tốc độ của con lắc: \(v=\sqrt{2gl\left( \cos \alpha -\cos {{\alpha }_{0}} \right)}\text{ }\)
Lời giải chi tiết:
Khi con lắc dao động với biên độ góc \({{\alpha }_{01}}={{5}^{0}}\), tốc độ của con lắc ở VTCB: \(v=\sqrt{2gl\left( 1-\cos {{\alpha }_{01}} \right)}\)
Giữ chặt điểm chính giữa của dây treo, chiều dài con lắc: \(l'=\frac{l}{2}\)
Tốc độ cực đại của con lắc lúc này: \({{v}_{\max }}=\sqrt{2gl'\left( 1-\cos {{\alpha }_{02}} \right)}=\sqrt{2g\frac{l}{2}\left( 1-\cos {{\alpha }_{02}} \right)}\)
Do tốc độ của con lắc không thay đổi, nên: \(v={{v}_{\max }}\)
\(\begin{align}& \Rightarrow \sqrt{2gl\left( 1-\cos {{\alpha }_{01}} \right)}=\sqrt{2g\frac{l}{2}\left( 1-\cos {{\alpha }_{02}} \right)}\Rightarrow 2\left( 1-\cos {{\alpha }_{01}} \right)=\left( 1-\cos {{\alpha }_{02}} \right) \\& \Rightarrow 2\left( 1-\cos {{5}^{0}} \right)=\left( 1-\cos {{\alpha }_{02}} \right)\Rightarrow \cos {{\alpha }_{02}}=0,9924\Rightarrow {{\alpha }_{02}}\approx 7,{{1}^{0}} \\\end{align}\)
Chọn A.
Câu hỏi 20 :
Một con lắc đơn có chiều dài 1 m, đầu trên cố định đầu dưới gắn với vật nặng có khối lượng m. Điểm cố định cách mặt đất 2,5 m. Ở thời điểm ban đầu đưa con lắc lệch khỏi vị trí cân bằng một góc \(\alpha =0,09\,\,rad\), rồi thả nhẹ. Khi con lắc vừa qua vị trí cân bằng thì sợi dây bị đứt. Bỏ qua mọi sức cản, lấy \(g=9,8\,\,m/{{s}^{2}}\). Tốc độ của vật nặng ở thời điểm t = 0,08 s có giá trị gần bằng
- A 0,35 m/s
- B 0,83 m/s
- C 0,57 m/s
- D 0,069 m/s
Đáp án: D
Phương pháp giải:
Chu kì dao động của con lắc: \(T=2\pi \sqrt{\frac{l}{g}}\)
Tốc độ của con lắc: \(v=\sqrt{2gl(cos\alpha -\cos {{\alpha }_{0}})}\text{ }\)
Lời giải chi tiết:
Chu kỳ dao động của con lắc: \(T=2\pi \sqrt{\frac{l}{g}}=2\pi \sqrt{\frac{1}{9,8}}=2\,\,\left( s \right)\)
Tần số góc của con lắc: \(\omega =\frac{2\pi }{T}=\frac{2\pi }{2}=\pi \,\,\left( rad/s \right)\)
Thời điểm sợi dây treo con lắc bị đứt là: \({{t}_{0}}=\frac{T}{4}=0,5\,\,\left( s \right)\)
Vậy thời điểm t = 0,08 s con lắc chưa bị đứt.
Phương trình dao động của con lắc: \(\alpha ={{\alpha }_{0}}cos\pi t\)
Tại thời điểm t = 0,08 s, con lắc có li độ góc:
\(\alpha ={{\alpha }_{0}}cos\pi t=0,09.cos\left( 0,08\pi \right)=0,087\,\,\left( rad \right)\)
Tốc độ của vật nặng khi đó:
\(v=\sqrt{2gl\left( \cos \alpha -\cos {{\alpha }_{0}} \right)}=\sqrt{2.9,8.1.(\cos 0,0872-\cos 0,09)}=0,069\,\,m/s\)
Chọn D.
Câu hỏi 21 :
Một con lắc đơn dao động điều hoà trong điện trường đều, có véc tơ cường độ điện trường có phương thẳng đứng, hướng xuống. Khi vật treo chưa tích điện thì chu kỳ dao động là \({T_0} = 2s\), khi vật treo lần lượt tích điện q1 và q2 thì chu kỳ dao động tương ứng là \({T_1} = 2,4s;{T_2} = 1,6s\). Tỉ số \(\dfrac{{{q_1}}}{{{q_2}}}\)là:
- A \( - \dfrac{{44}}{{81}}\)
- B \( - \dfrac{{81}}{{44}}\)
- C \( - \dfrac{{24}}{{57}}\)
- D \( - \dfrac{{57}}{{24}}\)
Đáp án: A
Phương pháp giải:
Chu kì dao động của con lắc đơn khi vật chưa tích điện: \({T_0} = 2\pi \sqrt {\dfrac{l}{g}} \)
Khi vật tích điện: \(T = 2\pi \sqrt {\dfrac{l}{{g'}}} \)
Với: \(g' = g \pm \dfrac{{\left| q \right|E}}{m}\)
Lời giải chi tiết:
Khi vật treo chưa tích điện: \({T_0} = 2\pi \sqrt {\dfrac{l}{g}} = 2s\)
Khi vật treo tích điện q1: \({T_1} = 2,4s > {T_0} \Rightarrow {T_1} = 2\pi \sqrt {\dfrac{l}{{g - \dfrac{{\left| {{q_1}} \right|E}}{m}}}} = 2,4s \Rightarrow {q_1} < 0\)
Khi vật treo tích điện q2: \({T_2} = 1,6s < {T_0} \Rightarrow {T_2} = 2\pi \sqrt {\dfrac{l}{{g + \dfrac{{\left| {{q_2}} \right|E}}{m}}}} = 1,6s \Rightarrow {q_2} > 0\)
Có: \(\left\{ \begin{array}{l}{\left( {\dfrac{{{T_0}}}{{{T_1}}}} \right)^2} = \dfrac{{g - \dfrac{{\left| {{q_1}} \right|E}}{m}}}{g} = \dfrac{{25}}{{36}} \Rightarrow \dfrac{{\left| {{q_1}} \right|E}}{m} = \dfrac{{11}}{{36}}.g\,\,\,\,\left( 1 \right)\\{\left( {\dfrac{{{T_0}}}{{{T_2}}}} \right)^2} = \dfrac{{g + \dfrac{{\left| {{q_2}} \right|E}}{m}}}{g} = \dfrac{{25}}{{16}} \Rightarrow \dfrac{{\left| {{q_2}} \right|E}}{m} = \dfrac{9}{{16}}.g\,\,\,\,\left( 2 \right)\end{array} \right.\)
Lấy \(\dfrac{{\left( 1 \right)}}{{\left( 2 \right)}} \Leftrightarrow \left| {\dfrac{{{q_1}}}{{{q_2}}}} \right| = \dfrac{{44}}{{81}} \Rightarrow \dfrac{{{q_1}}}{{{q_2}}} = - \dfrac{{44}}{{81}}\)
Chọn A.
Câu hỏi 22 :
Một con lắc đơn có khối lượng vật nặng là m = 100g, sợi dây mảnh. Từ vị trí cân bằng kéo vật sao cho dây treo hợp với phương thẳng đứng góc 600 rồi thả nhẹ. Lấy\(g = 10m/{s^2}\), bỏ qua mọi lực cản. Khi độ lớn gia tốc của con lắc có giá trị nhỏ nhất thì lực căng sợi dây có độ lớn
- A 1,5N.
- B 2,0N.
- C 0,5N.
- D 1,0N.
Đáp án: D
Phương pháp giải:
+ Lực căng dây: \(T = mg\left( {3.\cos \alpha - 2.\cos {\alpha _0}} \right)\)
+ Gia tốc của con lắc đơn:
Gia tốc tiếp tuyến: \({a_t} = - g.\sin \alpha \)
Gia tốc pháp tuyến: \({a_n} = 2g.\left( {\cos \alpha - \cos {\alpha _0}} \right)\)
Gia tốc toàn phần: \(a = \sqrt {a_t^2 + a_n^2} = \sqrt {{g^2}.{{\sin }^2}\alpha + 4{g^2}.{{\left( {\cos \alpha - \cos {\alpha _0}} \right)}^2}} \)
Lời giải chi tiết:
Gia tốc của con lắc đơn:
\(\begin{array}{*{20}{l}}
\begin{gathered}
a = \sqrt {a_t^2 + a_n^2} \hfill \\
\,\, = \sqrt {{g^2}.{{\sin }^2}\alpha + 4{g^2}.{{\left( {\cos \alpha - \cos {\alpha _0}} \right)}^2}} \hfill \\
\end{gathered} \\
\begin{gathered}
{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = g\sqrt {{{\sin }^2}\alpha + 4{{\left( {\cos \alpha - \cos 60} \right)}^2}} \hfill \\
\,\, = 10.\sqrt {{{\sin }^2}\alpha + 4\left( {{{\cos }^2}\alpha - \cos \alpha + {{0,5}^2}} \right)} \hfill \\
\end{gathered} \\
{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = 10\sqrt {{{\sin }^2}\alpha + 4{{\cos }^2}\alpha - 4\cos \alpha + 1} } \\
{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = 10\sqrt {{{\sin }^2}\alpha + {{\cos }^2}\alpha + 3{{\cos }^2}\alpha - 4\cos \alpha + 1} } \\
{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = 10\sqrt {3{{\cos }^2}\alpha - 4\cos \alpha + 2} }
\end{array}\)
Ta có: \(3{\cos ^2}\alpha - 4\cos \alpha + 2 = {\left( {\sqrt 3 \cos \alpha - \dfrac{2}{{\sqrt 3 }}} \right)^2} + \dfrac{2}{3} \ge \dfrac{2}{3}\)
\( \Rightarrow {a_{\min }} \Leftrightarrow {\left( {3{{\cos }^2}\alpha - 4\cos \alpha + 2} \right)_{\min }} = \dfrac{2}{3}\)
Dấu “=” xảy ra khi \(\sqrt 3 \cos \alpha = \dfrac{2}{{\sqrt 3 }} \Rightarrow \cos \alpha = \dfrac{2}{3}\)
Khi đó lực căng dây có độ lớn:
\(T = mg\left( {3.\cos \alpha - 2.\cos {\alpha _0}} \right) = 0,1.10.\left( {3.\dfrac{2}{3} - 2.\cos 60} \right) = 1N\)
Chọn D.
Câu hỏi 23 :
Con lắc đơn gồm vật nhỏ có khối lượng \(1g\) treo vào sợi dây nhẹ, không dãn, tại nơi có \(g = 10m/{s^2}\), trong điện trường đều có vecto cường độ điện trường E nằm ngang, độ lớn \(E = 1000V/m\). Khi vật chưa tích điện, chu kì dao động điều hòa của con lắc là \(T\). Khi con lắc tích điện \(q\), chu kì dao động điều hòa của con lắc là \(0,841T\). Độ lớn điện tích \(q\) là
- A \(\sqrt 2 {.10^{ - 2}}C.\)
- B \(\sqrt 2 {.10^{ - 5}}C\)
- C \({10^{ - 2}}C.\)
- D \({10^{ - 5}}C.\)
Đáp án: D
Phương pháp giải:
+ Áp dụng công thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{l}{g}} \)
+ Áp dụng bài toán con lắc đơn chịu thêm tác dụng của lực điện
Lời giải chi tiết:
Ta có:
- Khi con lắc chưa tích điện, chu kì dao động của con lắc \(T = 2\pi \sqrt {\dfrac{l}{g}} \)
- Khi con lắc tích điện, đặt trong điện trường nằm ngang thì nó chịu thêm tác dụng của lực điện
+ \(\overrightarrow E \) có phương ngang =>\(\overrightarrow {{F_d}} \) có phương ngang
+ Chu kì dao động của con lắc tích điện q đặt trong điện trường đều là: \(T' = 2\pi \sqrt {\dfrac{l}{{g'}}} \)
Ta có:
\(\begin{array}{l}a = \dfrac{{{F_d}}}{m} = \dfrac{{\left| q \right|E}}{m}\\g' = \sqrt {{g^2} + {a^2}} \\ \to T' = 2\pi \sqrt {\dfrac{l}{{g'}}} = 2\pi \sqrt {\dfrac{l}{{\sqrt {{g^2} + {a^2}} }}} \end{array}\)
Ta suy ra: \(\dfrac{T}{{T'}} = \sqrt {\dfrac{{g'}}{g}} \)
\(\begin{array}{l} \Leftrightarrow \dfrac{T}{{0,841T}} = \sqrt {\dfrac{{\sqrt {{g^2} + {a^2}} }}{g}} \\ \Rightarrow {\left( {\dfrac{1}{{0,841}}} \right)^2}.10 = \sqrt {{{10}^2} + {a^2}} \\ \Rightarrow a = 9,995m/{s^2}\\ \Leftrightarrow \dfrac{{\left| q \right|E}}{m} = 9,995\\ \Rightarrow \left| q \right| = 9,{995.10^{ - 6}} \approx {10^{ - 5}}C\end{array}\)
Chọn D
Câu hỏi 24 :
Một con lắc đơn gồm dây treo có chiều dài 1 m và vật nhỏ có khối lượng 100 g mang điện tích 2.10-5 C. Treo con lắc đơn này trong điện trường đều với vectơ cường độ điện trường hướng theo phương ngang và có độ lớn 5.104 V/m. Trong mặt phẳng thẳng đứng đi qua điểm treo và song song với vectơ cường độ điện trường, kéo vật nhỏ theo chiều của vectơ cường độ điện trường sao cho dây treo hợp với vectơ gia tốc trong trường \(\overrightarrow g \) một góc 550 rồi buông nhẹ cho con lắc dao động điều hòa. Lấy g = 10 m/s2. Trong quá trình dao động, tốc độ cực đại của vật nhỏ là
- A 0,50 m/s
- B 0,66 m/s
- C 2,87 m/s
- D 3,41 m/s
Đáp án: B
Phương pháp giải:
Ở vị trí cân bằng, dây treo hợp với phương thẳng đứng một góc: \(\tan \theta = \dfrac{{qE}}{{mg}}\)
Biên độ góc của con lắc: \({\alpha _0} = \alpha - \theta \)
Gia tốc trọng trường hiệu dụng: \({g_{HD}} = \dfrac{g}{{\cos \theta }}\)
Tốc độ cực đại của con lắc: \({v_{\max }} = \sqrt {2{g_{HD}}{\rm{l}}\left( {1 - \cos {\alpha _0}} \right)} \)
Lời giải chi tiết:
Cách giải:
Ở vị trí cân bằng, dây treo hợp với phương thẳng đứng một góc:
\(\tan \theta = \dfrac{{qE}}{{mg}} = \dfrac{{{{2.10}^{ - 5}}{{.5.10}^4}}}{{0,1.10}} = 1 \Rightarrow \theta = {45^0}\)
Biên độ góc của con lắc là: \({\alpha _0} = \alpha - \theta = {55^0} - {45^0} = {10^0}\)
Gia tốc trọng trường hiệu dụng là: \({g_{HD}} = \dfrac{g}{{\cos \theta }} = \dfrac{{10}}{{\cos {{45}^0}}} = 10\sqrt 2 \,\,\left( {m/{s^2}} \right)\)
Tốc độ cực đại của con lắc là:
\({v_{\max }} = \sqrt {2{g_{HD}}{\rm{l}}\left( {1 - \cos {\alpha _0}} \right)} = \sqrt {2.10\sqrt 2 .1.\left( {1 - \cos {{10}^0}} \right)} = 0,66\,\,\left( {m/s} \right)\)
Chọn B.
Câu hỏi 25 :
Con lắc đơn gồm vật nhỏ khối lượng 50 g, mang điện tích 10-6C, được treo vào sợi dây mảnh, nhẹ, cách điện, không giãn chiều dài 1 m. Toàn bộ hệ thống đặt trong điện trường đều nằm ngang, cường độ 73500 V/m. Ban đầu dây treo được giữ theo phương thẳng đứng, thả nhẹ cho vật dao động. Lấy \(g = 9,8\,\,m/{s^2}\) Khi dây treo lệch góc 30 thì tốc độ của vật là
- A 0,436 m/s.
- B 0,439 m/s.
- C 0,355 m/s.
- D 0,357 m/s.
Đáp án: D
Phương pháp giải:
Gia tốc trọng trường hiệu dụng: \(\overrightarrow {g'} = \overrightarrow g + \dfrac{{\overrightarrow {{F_d}} }}{m}\)
Vị trí cân bằng là vị trí dây treo song song với \(\overrightarrow {g'} \)
Tốc độ của vật:\(v = \sqrt {g'l(\alpha _O^2 - {\alpha ^2})} \)
Lời giải chi tiết:
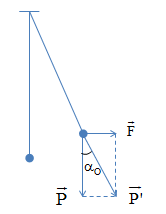
Lực điện tác dụng lên vật theo phương ngang là:
\(\begin{array}{l}F = E.q = {73500.10^{ - 6}} = 0,0735\,\,\left( N \right)\\ \Rightarrow \tan {\alpha _O} = \dfrac{F}{P} = \dfrac{{0,0735}}{{0,5.9,8}} = 0,15\end{array}\)
Do góc lệch nhỏ, \({\alpha _O} = \tan {\alpha _O} = 0,15\)
Gia tốc trọng trường hiệu dụng là: \(g' = \sqrt {{g^2} + {{\left( {\dfrac{F}{m}} \right)}^2}} = 9,91\)
Khi dây lệch góc 30, ta có: \(\alpha = {\alpha _O} - \dfrac{{3.\pi }}{{180}} = 0,05\)
Tốc độ của vật là:\(v = \sqrt {g'l(\alpha _O^2 - {\alpha ^2})} = 0,357\,\,\left( {m/s} \right)\)
Chọn D.
Câu hỏi 26 :
Một toa xe trượt không ma sát trên một đường dốc xuống dưới, góc nghiêng của dốc so với mặt phẳng nằm ngang là \(\alpha = {45^0}\). Treo lên trần toa xe một con lắc đơn gồm dây treo có chiều dài l = 1 m nối với một quả cầu nhỏ. Trong thời gian xe trượt xuống, kích thích cho con lắc dao động điều hòa với biên độ góc nhỏ. Bỏ qua ma sát, lấy \(g = 10\,\,m/{s^2}\). Chu kì dao động của con lắc là
- A 2,13 s
- B 2,36 s
- C 1,18 s
- D 2,81 s
Đáp án: B
Phương pháp giải:
Chu kì của con lắc khi xe trượt không ma sát: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{{g\cos \alpha }}} \)
Lời giải chi tiết:
Chu kì của con lắc là:
\(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{{g\cos \alpha }}} = 2\pi \sqrt {\dfrac{1}{{10.cos{{45}^0}}}} \approx 2,36\,\,\left( s \right)\)
Chọn B.
Câu hỏi 27 :
Một toa xe trượt không ma sát trên một đường dốc xuống dưới, góc nghiêng của dốc so với mặt phẳng nằm ngang là \(\alpha = {30^0}\). Treo lên trần toa xe một con lắc đơn gồm dây treo có chiều dài 0,5 m nối với một quả cầu nhỏ. Trong thời gian xe trượt xuống, kích thích cho con lắc dao động điều hòa với biên độ góc nhỏ. Bỏ qua ma sát, lấy \(g = 10\,\,m/{s^2}\). Chu kì dao động của con lắc là
- A 2,05 s
- B 1,36 s
- C 1,51 s
- D 1,18 s
Đáp án: C
Phương pháp giải:
Chu kì của con lắc khi xe trượt không ma sát: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{{g\cos \alpha }}} \)
Lời giải chi tiết:
Chu kì của con lắc là:
\(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{{g\cos \alpha }}} = 2\pi \sqrt {\dfrac{{0,5}}{{10.cos{{30}^0}}}} \approx 1,51\,\,\left( s \right)\)
Chọn C.
Câu hỏi 28 :
Một toa xe trượt trên một đường dốc xuống dưới, góc nghiêng của dốc so với mặt phẳng nằm ngang là \(\alpha = {30^0}\). Treo lên trần toa xe một con lắc đơn gồm dây treo có chiều dài 0,5 m nối với một quả cầu nhỏ. Trong thời gian xe trượt xuống, kích thích cho con lắc dao động điều hòa với biên độ góc nhỏ. Hệ số ma sát của xe với mặt phẳng nghiêng là 0,1. Lấy \(g = 10\,\,m/{s^2}\). Chu kì dao động của con lắc là
- A 1,95 s
- B 2,36 s
- C 1,15 s
- D 1,43 s
Đáp án: D
Phương pháp giải:
Chu kì của con lắc khi xe trượt có ma sát: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{{g\cos \alpha \sqrt {1 + {\mu ^2}} }}} \)
Lời giải chi tiết:
Chu kì của con lắc là:
\(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{{g\cos \alpha \sqrt {1 + {\mu ^2}} }}} = 2\pi \sqrt {\dfrac{{0,5}}{{10.cos{{30}^0}\sqrt {1 + 0,{5^2}} }}} \approx 1,43\,\,\left( s \right)\)
Chọn D.
Câu hỏi 29 :
Một con lắc đơn dao động điều hòa với chu kì T tại nơi có thêm trường ngoại lực có độ lớn F theo phương ngang. Nếu quay phương của ngoại lực một góc \(\alpha \left( {{0^0} < \alpha < {{90}^0}} \right)\) trong mặt phẳng thẳng đứng và giữ nguyên độ lớn thì chu kì dao động là \({T_1} = 2,5\,\,s\) hoặc \({T_2} = 1,6\,\,s\). Chu kì T gần nhất giá trị nào sau đây?
- A 1,83 s
- B 1,93 s
- C 2,92 s
- D 2,18 s
Đáp án: A
Phương pháp giải:
Gia tốc hiệu dụng của con lắc khi ngoại lực hướng theo phương ngang: \({g_0} = \sqrt {{g^2} + {a^2}} \)
Gia tốc hiệu dụng của con lắc khi ngoại lực hợp với phương thẳng đứng góc β:
\(g' = \sqrt {{g^2} + {a^2} - 2g.a.cos\beta } \)
Chu kì của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{g}} \)
Lời giải chi tiết:
Nhận xét: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{g}} \Rightarrow {T^2} = 4{\pi ^2}\dfrac{{\rm{l}}}{g} \Rightarrow {T^2} \sim \dfrac{1}{g}\) hay \(g \sim \dfrac{1}{{{T^2}}}\)
Ban đầu \(\overrightarrow F \) theo phương ngang, gia tốc hiệu dụng: \({g_0} = \sqrt {{g^2} + {a^2}} \)
Trường hợp 1: \(\overrightarrow F \) hướng lên trên:
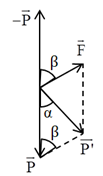
Ta có: \(\beta = {90^0} - \alpha \Rightarrow \cos \beta = - \sin \alpha \)
Gia tốc hiệu dụng là: \({g_1} = \sqrt {{g^2} + {a^2} + 2g.a.\sin \alpha } \)
\( \Rightarrow {g_1}^2 = {g^2} + {a^2} + 2g.a.\sin \alpha \,\,\left( 1 \right)\)
Trường hợp 2: \(\overrightarrow F \) hướng xuống dưới:
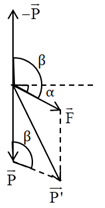
Ta có: \(\beta = {90^0} + \alpha \Rightarrow \cos \beta = \sin \alpha \)
Gia tốc hiệu dụng là: \({g_2} = \sqrt {{g^2} + {a^2} - 2g.a.\sin \alpha } \)
\( \Rightarrow {g_2}^2 = {g^2} + {a^2} - 2g.a.\sin \alpha \,\,\left( 2 \right)\)
Từ (1) và (2) ta có: \({g_1}^2 + {g_2}^2 = 2\left( {{g^2} + {a^2}} \right)\)
\( \Rightarrow \dfrac{1}{{{T_1}^4}} + \dfrac{1}{{{T_2}^4}} = \dfrac{2}{{{T_0}^4}} \Rightarrow \dfrac{1}{{2,{5^4}}} + \dfrac{1}{{1,{6^4}}} = \dfrac{2}{{{T_0}^4}} \Rightarrow {T_0} \approx 1,83\,\,\left( s \right)\)
Chọn A.
Câu hỏi 30 :
Một con lắc đơn chiều dài 100 cm, khối lượng 0,1 kg, dao động điều hòa tại nơi có thêm trường ngoại lực có độ lớn 0,53 N, hướng lên và hợp với phương ngang một góc \(\alpha = {60^0}\). Lấy \(g = 10\,\,m/{s^2}\). Chu kì của con lắc đơn là
- A 1,91 s
- B 1,13 s
- C 2,56 s
- D 2,23 s
Đáp án: C
Phương pháp giải:
Gia tốc hiệu dụng của con lắc khi ngoại lực hợp với phương thẳng đứng góc β:
\(g' = \sqrt {{g^2} + {{\left( {\dfrac{F}{m}} \right)}^2} - 2g.\dfrac{F}{m}.cos\beta } \)
Chu kì của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{{g'}}} \)
Lời giải chi tiết:
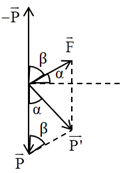
Gia tốc trọng trường hiệu dụng của con lắc là:
\(\begin{array}{l}g' = \sqrt {{g^2} + {{\left( {\dfrac{F}{m}} \right)}^2} - 2g.\dfrac{F}{m}.cos\left( {{{90}^0} - \alpha } \right)} \\ \Rightarrow g' = \sqrt {{{10}^2} + {{\left( {\dfrac{{0,53}}{{0,1}}} \right)}^2} - 2.10.\dfrac{{0,53}}{{0,1}}.cos{{30}^0}} = 6,02\,\,\left( {m/{s^2}} \right)\end{array}\)
Chu kì của con lắc đơn là: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{{g'}}} = 2\pi \sqrt {\dfrac{1}{{6,02}}} = 2,56\,\,\left( s \right)\)
Chọn C.
Câu hỏi 31 :
Một con lắc đơn chiều dài 100 cm, khối lượng 0,15 kg, dao động điều hòa tại nơi có thêm trường ngoại lực có độ lớn 0,75 N, hướng xuống và hợp với phương ngang một góc \(\alpha = {30^0}\). Lấy \(g = 10\,\,m/{s^2}\). Chu kì của con lắc đơn là
- A 2,91 s
- B 1,73 s
- C 1,62 s
- D 2,12 s
Đáp án: B
Phương pháp giải:
Gia tốc hiệu dụng của con lắc khi ngoại lực hợp với phương thẳng đứng góc β:
\(g' = \sqrt {{g^2} + {{\left( {\dfrac{F}{m}} \right)}^2} - 2g.\dfrac{F}{m}.cos\beta } \)
Chu kì của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{{g'}}} \)
Lời giải chi tiết:
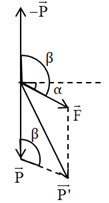
Gia tốc trọng trường hiệu dụng của con lắc là:
\(\begin{array}{l}g' = \sqrt {{g^2} + {{\left( {\dfrac{F}{m}} \right)}^2} + 2g.\dfrac{F}{m}.cos\left( {{{90}^0} + \alpha } \right)} \\ \Rightarrow g' = \sqrt {{{10}^2} + {{\left( {\dfrac{{0,75}}{{0,15}}} \right)}^2} - 2.10.\dfrac{{0,75}}{{0,15}}.cos{{120}^0}} = 13,23\,\,\left( {m/{s^2}} \right)\end{array}\)
Chu kì của con lắc đơn là: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{{g'}}} = 2\pi \sqrt {\dfrac{1}{{13,23}}} = 1,73\,\,\left( s \right)\)
Chọn C.
Câu hỏi 32 :
Con lắc đơn gồm một hòn bi có khối lượng m treo trên sợi dây dài l = 1 m ở tại nơi có gia tốc trọng trường g = 9,8 m/s2. Bỏ qua mọi ma sát và lực cản môi trường. Con lắc trên được treo vào trần một ô tô chuyển động nhanh dần đều với gia tốc a = 2 m/s2 từ đỉnh mặt phẳng nghiêng với mặt phẳng ngang một góc 300. Hỏi con lắc dao động với chu kì bằng bao nhiêu
- A 3,569 s
- B 1,898 s
- C 3,028 s
- D 2,098 s
Đáp án: D
Phương pháp giải:
Lực quán tính tác dụng lên con lắc: \(\overrightarrow {{F_{qt}}} = - m\overrightarrow a \)
Gia tốc trọng trường hiệu dụng tác dụng lên con lắc: \(g' = \sqrt {{g^2} + {{\left( {\dfrac{F}{m}} \right)}^2} - 2g.\dfrac{F}{m}\cos \beta } \)
Chu kì của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{{g'}}} \)
Lời giải chi tiết:
Ô tô đi xuống nhanh dần đều, lực quán tính tác dụng lên con lắc hướng lên. Ta có hình vẽ:
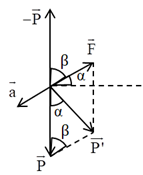
Gia tốc trọng trường hiệu dụng tác dụng lên con lắc là:
\(\begin{array}{l}g' = \sqrt {{g^2} + {{\left( {\dfrac{F}{m}} \right)}^2} - 2g.\dfrac{F}{m}\cos \beta } = \sqrt {{g^2} + {a^2} - 2g.a\cos \left( {{{90}^0} - \alpha } \right)} \\ \Rightarrow g' = \sqrt {9,{8^2} + {2^2} - 2.9,8.2.cos{{60}^0}} = 8,97\,\,\left( {m/{s^2}} \right)\end{array}\)
Chu kì của con lắc là:
\(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{{g'}}} = 2\pi \sqrt {\dfrac{1}{{8,97}}} = 2,098\,\,\left( s \right)\)
Chọn D.
Câu hỏi 33 :
Một con lắc đơn có dây dài l, vật nặng có khối lượng m = 100 g tích điện \(q = + {5.10^{ - 6}}\,\,C\) đặt trong điện trường đều có cường độ E = 105 V/m và các đường sức hướng xiên góc \(\alpha = {45^0}\) xuống dưới so với phương ngang. Bỏ qua mọi ma sát. Tính chu kì của con lắc trong điện trường biết chu kì của con lắc trong không khí là T = 2 s. Lấy \(g = 10\,\,m/{s^2}\) và \({\pi ^2} = 10\)
- A 1,4 s
- B 1,69 s
- C 0,5 s
- D 2,14 s
Đáp án: B
Phương pháp giải:
Gia tốc trọng trường hiệu dụng: \(g' = \sqrt {{g^2} + {{\left( {\dfrac{{\left| q \right|E}}{m}} \right)}^2} - 2g\dfrac{{\left| q \right|E}}{m}\cos \beta } \)
Chu kì của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{g}} \)
Lời giải chi tiết:
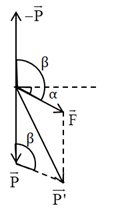
Từ hình vẽ, ta thấy: \(\beta = {90^0} + \alpha = {90^0} + {45^0} = {135^0}\)
Gia tốc trọng trường hiệu dụng là:
\(\begin{array}{l}g' = \sqrt {{g^2} + {{\left( {\dfrac{{\left| q \right|E}}{m}} \right)}^2} - 2g\dfrac{{\left| q \right|E}}{m}\cos \beta } \\ \Rightarrow g' = \sqrt {{{10}^2} + {{\left( {\dfrac{{{{5.10}^{ - 6}}{{.10}^5}}}{{0,1}}} \right)}^2} - 2.10.\dfrac{{{{5.10}^{ - 6}}{{.10}^5}}}{{0,1}}.cos{{135}^0}} \\ \Rightarrow g' \approx 14\,\,\left( {m/{s^2}} \right)\end{array}\)
Chu kì của con lắc trong 2 trường hợp là:
\(\begin{array}{l}\left\{ \begin{array}{l}T = 2\pi \sqrt {\dfrac{{\rm{l}}}{g}} \\T' = 2\pi \sqrt {\dfrac{{\rm{l}}}{{g'}}} \end{array} \right. \Rightarrow \dfrac{{T'}}{T} = \sqrt {\dfrac{g}{{g'}}} \\ \Rightarrow \dfrac{{T'}}{2} = \sqrt {\dfrac{{10}}{{14}}} \Rightarrow T' = 1,69\,\,\left( s \right)\end{array}\)
Chọn B.
Câu hỏi 34 :
Một con lắc đơn có dây dài l, vật nặng có khối lượng m = 250 g, chu kì T = 2 s. Tích điện cho con lắc điện tích \(q = + {2.10^{ - 6}}\,\,C\) đặt trong điện trường đều có cường độ \(E = {2.10^5}\,\,V/m\) và các đường sức xiên góc \(\alpha = {45^0}\) hướng lên so với phương ngang. Bỏ qua mọi ma sát. Tính chu kì của con lắc. Lấy \(g = 10\,\,m/{s^2}\).
- A 2,237 s
- B 2,165 s
- C 1,926 s
- D 1,593 s
Đáp án: A
Phương pháp giải:
Gia tốc trọng trường hiệu dụng: \(g' = \sqrt {{g^2} + {{\left( {\dfrac{{\left| q \right|E}}{m}} \right)}^2} - 2g\dfrac{{\left| q \right|E}}{m}\cos \beta } \)
Chu kì của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{g}} \)
Lời giải chi tiết:
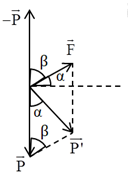
Từ hình vẽ, ta thấy: \(\beta = {90^0} - \alpha = {90^0} - {45^0} = {45^0}\)
Gia tốc trọng trường hiệu dụng là:
\(\begin{array}{l}g' = \sqrt {{g^2} + {{\left( {\dfrac{{\left| q \right|E}}{m}} \right)}^2} - 2g\dfrac{{\left| q \right|E}}{m}\cos \beta } \\ \Rightarrow g' = \sqrt {{{10}^2} + {{\left( {\dfrac{{{{2.10}^{ - 6}}{{.2.10}^5}}}{{0,25}}} \right)}^2} - 2.10.\dfrac{{{{2.10}^{ - 6}}{{.2.10}^5}}}{{0,25}}.cos{{45}^0}} \\ \Rightarrow g' \approx 8,94\,\,\left( {m/{s^2}} \right)\end{array}\)
Chu kì của con lắc trong 2 trường hợp là:
\(\begin{array}{l}\left\{ \begin{array}{l}T = 2\pi \sqrt {\dfrac{{\rm{l}}}{g}} \\T' = 2\pi \sqrt {\dfrac{{\rm{l}}}{{g'}}} \end{array} \right. \Rightarrow \dfrac{{T'}}{T} = \sqrt {\dfrac{g}{{g'}}} \\ \Rightarrow \dfrac{{T'}}{2} = \sqrt {\dfrac{{10}}{{8,94}}} \Rightarrow T' = 2,237\,\,\left( s \right)\end{array}\)
Chọn A.
Câu hỏi 35 :
Một con lắc đơn gồm dây treo có chiều dài 1m và vật nhỏ có khối lượng 100g mang điện tích 2.10-5C. Treo con lắc đơn này vào trong điện trường đều cường độ điện trường hướng theo hương ngang và có độ lớn 5.104 V/m. Trong mặt phẳng thẳng đứng đi qua điểm treo và song song với vecto cường độ điện trường, kéo vật nhỏ theo chiều của vectơ cường độ điện trường sao cho dây treo hợp với vectơ gia tốc trọng trường một góc 540 rồi buông nhẹ cho con lắc dao động điều hoà. Lấy g = 10m/s2. Tốc độ của vật khi sợi dây lệch góc 400 so với phương thẳng đứng theo chiều của vectơ cường độ điện trường là:
- A 0,59m/s
- B 3,41m/s
- C 2,78 m/s
- D 0,49m/s
Đáp án: D
Phương pháp giải:
Gia tốc trọng trường hiệu dụng: \(g' = \sqrt {{g^2} + {{\left( {\dfrac{{qE}}{m}} \right)}^2}} \)
Tốc độ của vật: \(v = \sqrt {2g'.l.\left( {\cos \alpha ' - \cos {\alpha _0}} \right)} \)
Lời giải chi tiết:
Do \(\overrightarrow E \) có phương ngang nên \(\overrightarrow F \)cũng có phương ngang và \(\overrightarrow F \bot \overrightarrow P \)
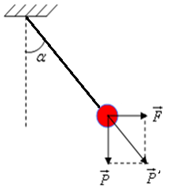
Tại VTCB góc lệch của dây treo so với phương thẳng đứng là:
\(\tan \alpha = \dfrac{F}{P} = \dfrac{{qE}}{{mg}} = \dfrac{{{{2.10}^{ - 5}}{{.5.10}^4}}}{{0,1.10}} = 1 \Rightarrow \alpha = {45^0}\)
Kéo vật nhỏ theo chiều của vectơ cường độ điện trường sao cho dây treo hợp với vectơ gia tốc trọng trường một góc 540 rồi buông nhẹ
→ Biên độ góc là: \({\alpha _0} = {54^0} - \alpha = {54^0} - {45^0} = {9^0}\)
Gia tốc trong trường hiệu dụng là:
\(g' = \sqrt {{g^2} + {{\left( {\dfrac{{qE}}{m}} \right)}^2}} = \sqrt {{{10}^2} + {{\left( {\dfrac{{{{2.10}^{ - 5}}{{.5.10}^4}}}{{0,1}}} \right)}^2}} = 10\sqrt 2 m/{s^2}\)
Tại vị trí sợi dây lệch góc 400 so với phương thẳng đứng theo chiều của vectơ cường độ điện trường có li độ góc là: \(\alpha ' = 40 - \alpha = 40 - 45 = - {5^0}\)
Tốc độ của vật tại đó là:
\(\begin{array}{l}v = \sqrt {2g'.l.\left( {\cos \alpha ' - \cos {\alpha _0}} \right)} \\ \Rightarrow v = \sqrt {2.10\sqrt 2 .1.\left( {\cos 5 - \cos 9} \right)} = 0,49m/s\end{array}\)
Chọn D.
Câu hỏi 36 :
Một con lắc đơn gồm hòn bi nhỏ bằng kim loại được tích điện q > 0. Khi đặt con lắc vào trong điện trường đều có véc tơ cường độ điện trường nằm ngang thì tại vị trí cân bằng dây treo hợp với phương thẳng đứng một góc α, có \(\tan \alpha = \dfrac{3}{4}\); lúc này con lắc dao động nhỏ với chu kỳ T1. Nếu đổi chiều điện trường này sao cho véctơ cường độ diện trường có phương thẳng đứng hướng lên và cường độ không đổi thì chu kỳ dao động nhỏ của con lắc lúc này là:
- A \({T_2} = {T_1}\sqrt {\dfrac{7}{5}} \)
- B \({T_2} = \dfrac{{{T_1}}}{{\sqrt 5 }}\)
- C \({T_2} = {T_1}\sqrt {\dfrac{5}{7}} \)
- D \({T_2} = {T_1}\sqrt 5 \)
Đáp án: D
Phương pháp giải:
\(\begin{array}{l}\overrightarrow {{F_d}} = q.\overrightarrow E = m.\overrightarrow a \\\overrightarrow {{F_d}} \bot \overrightarrow P \Rightarrow g' = \sqrt {{g^2} + {a^2}} \\\overrightarrow {{F_d}} \uparrow \uparrow \overrightarrow P \Rightarrow g' = g + a\\\overrightarrow {{F_d}} \uparrow \downarrow \overrightarrow P \Rightarrow g' = g - a\\T = 2\pi \sqrt {\dfrac{l}{{g'}}} \end{array}\)
Lời giải chi tiết:
Khi vecto cường độ điện trường nằm ngang:
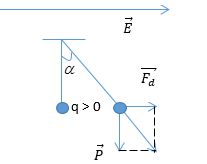
Từ hình vẽ ta có: \(\tan \alpha = \dfrac{{{F_d}}}{P} = \dfrac{{ma}}{{mg}} = \dfrac{3}{4} \Rightarrow a = \dfrac{3}{4}.g\)
Gia tốc trọng trường hiệu dụng :
\(g' = \sqrt {{g^2} + {a^2}} = \sqrt {{g^2} + \dfrac{{9{g^2}}}{{16}}} = \dfrac{5}{4}.g\)
Chu kì dao động của con lắc khi đó:
\({T_1} = 2\pi \sqrt {\dfrac{l}{{g'}}} = \dfrac{2}{{\sqrt 5 }}.2\pi \sqrt {\dfrac{l}{g}} \,\,\,\,\left( 1 \right)\)
+ Khi đổi chiều điện trường sao cho hướng vecto cường độ điện trường hướng lên thì \(\overrightarrow {{F_d}} \) hướng lên (do q > 0). Gia tốc trọng trường hiệu dụng khi đó:
\(g'' = g - a = g - \dfrac{3}{4}.g = \dfrac{1}{4}.g\)
Chu kì dao động của con lắc khi đó:
\({T_2} = 2\pi \sqrt {\dfrac{l}{{g''}}} = 2.2\pi \sqrt {\dfrac{l}{g}} \,\,\,\,\,\left( 2 \right)\)
+ Từ (1) và (2) ta có: \(\dfrac{{{T_2}}}{{{T_1}}} = \sqrt 5 \Rightarrow {T_2} = \sqrt 5 .{T_1}\)
Chọn D.
Câu hỏi 37 :
Một con lắc đơn dao động với biên độ \({\alpha _0} < \dfrac{\pi }{2}\), có mốc thế năng được chọn tại vị trí cân bằng của vật nặng. Gọi độ lớn vận tốc của vật nặng khi động năng bằng thế năng là v1, khi độ lớn của lực căng dây treo bằng trọng lực tác động lên vật là v2 . Tỉ số \(\dfrac{{{v_1}}}{{{v_2}}}\) có giá trị nào sau đây?
- A \(\dfrac{3}{2}\)
- B \(\dfrac{2}{3}\)
- C \(\sqrt {\dfrac{2}{3}} \)
- D \(\sqrt {\dfrac{3}{2}} \)
Đáp án: D
Phương pháp giải:
Công thức tính độ lớn vận tốc và lực căng dây: \(\left\{ \begin{array}{l}v = \sqrt {2gl\left( {\cos \alpha - \cos {\alpha _0}} \right)} \\T = mg.\left( {3\cos \alpha - 2\cos {\alpha _0}} \right)\end{array} \right.\)
Công thức tính cơ năng, thế năng và động năng: \(\left\{ \begin{array}{l}{\rm{W}} = mgl.\left( {1 - \cos {\alpha _0}} \right)\\{{\rm{W}}_t} = mgl.\left( {1 - \cos \alpha } \right)\\{{\rm{W}}_d} = {\rm{W}} - {{\rm{W}}_t}\end{array} \right.\)
Theo bài ra ta có: \(\left\{ \begin{array}{l}{{\rm{W}}_t} = {{\rm{W}}_d} \Rightarrow {v_1}\\T = P \Rightarrow {v_2}\end{array} \right. \Rightarrow \dfrac{{{v_1}}}{{{v_2}}}\)
Lời giải chi tiết:
+ Khi động năng bằng thế năng:
\(\begin{array}{l}{{\rm{W}}_t} = {\rm{W}} - {{\rm{W}}_t}\\ \Leftrightarrow mgl.\left( {1 - \cos {\alpha _1}} \right) = mgl.\left( {1 - \cos {\alpha _0}} \right) - mgl.\left( {1 - \cos {\alpha _1}} \right)\\ \Leftrightarrow 1 - \cos {\alpha _1} = \cos {\alpha _1} - \cos {\alpha _0}\\ \Leftrightarrow \cos {\alpha _1} = \dfrac{1}{2} + \dfrac{1}{2}.\cos {\alpha _0}\end{array}\)
+ Khi độ lớn của lực căng dây treo bằng trọng lực tác động lên vật:
\(\begin{array}{l}mg.\left( {3\cos {\alpha _2} - 2\cos {\alpha _0}} \right) = mg\\ \Leftrightarrow 3\cos {\alpha _2} - 2\cos {\alpha _0} = 1 \Leftrightarrow \cos {\alpha _2} = \dfrac{1}{3} + \dfrac{2}{3}.\cos {\alpha _0}\end{array}\)
+ Suy ra:
\(\begin{array}{l}\dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{\sqrt {2gl\left( {\cos {\alpha _1} - \cos {\alpha _0}} \right)} }}{{\sqrt {2gl\left( {\cos {\alpha _2} - \cos {\alpha _0}} \right)} }} = \sqrt {\dfrac{{\cos {\alpha _1} - \cos {\alpha _0}}}{{\cos {\alpha _2} - \cos {\alpha _0}}}} \\\,\,\,\,\,\,\, = \sqrt {\dfrac{{\dfrac{1}{2} + \dfrac{1}{2}.\cos {\alpha _0} - \cos {\alpha _0}}}{{\dfrac{1}{3} + \dfrac{2}{3}.\cos {\alpha _0} - \cos {\alpha _0}}}} = \sqrt {\dfrac{{\dfrac{1}{2}\left( {1 - \cos {\alpha _0}} \right)}}{{\dfrac{1}{3}\left( {1 - \cos {\alpha _0}} \right)}}} = \sqrt {\dfrac{3}{2}} \end{array}\)
Chọn D.
Câu hỏi 38 :
Một con lắc đơn có khối lượng vật nặng là m, sợi dây mảnh có chiều dài l. Từ vị trí cân bằng kéo vật sao cho dây treo hợp với phương thẳng đứng góc 50 rồi thả nhẹ. Lấy g = 9,8m/s2. Trong quá trình chuyển động thì gia tốc tiếp tuyến lớn nhất của vật là
- A 19,600m/s2
- B 9,397m/s2
- C 0,490m/s2
- D 0,854m/s2.
Đáp án: D
Phương pháp giải:
Đối với con lắc đơn, ta có hình vẽ.
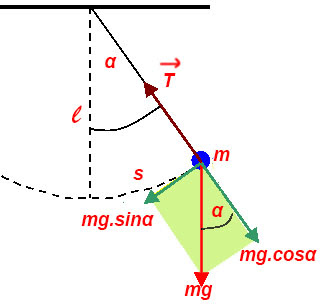
Gia tốc tiếp tuyến là do thành phần P.sinα gây ra, tức là
\({a_t} = g.\sin \alpha \)
Lời giải chi tiết:
Đối với con lắc đơn, ta có hình vẽ.
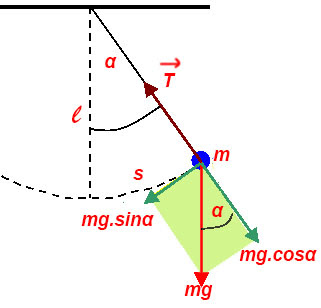
Gia tốc tiếp tuyến là do thành phần P.sinα gây ra, tức là:
Để gia tốc tiếp tuyến lớn nhất thì góc α lớn nhất và bằng 50.
Vậy:
\({a_{tmax}} = \left| {g.\sin {5^0}} \right| = 0,854m/{s^2}\)
Chọn D.
Câu hỏi 39 :
Một con lắc đơn có vật nhỏ mang điện tích dương được treo ở một nơi trên mặt đất trong điện trường đều có cường độ điện trường \(\overrightarrow E \). Khi \(\overrightarrow E \) hướng thẳng đứng xuống dưới thì con lắc dao động điều hòa với chu kì T1. Khi \(\overrightarrow E \) có phương nằm ngang thì con lắc dao động điều hòa với chu kì T2. Biết trong hai trường hợp, độ lớn cường độ điện trường bằng nhau. Tỉ số \(\dfrac{{{T_2}}}{{{T_1}}}\) có thể nhận giá trị nào sau đây?
- A 0,89.
- B 1,23.
- C 0,96.
- D 1,15.
Đáp án: D
Phương pháp giải:
Gia tốc trọng trường của con lắc chịu tác dụng của ngoại lực: \(\overrightarrow {{g_{HD}}} = \overrightarrow g + \overrightarrow a \)
Chu kì của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{{{g_{HD}}}}} \)
Bất đẳng thức Cô – si: \({a^2} + {b^2} \ge 2ab\) (dấu “=” xảy ra \( \Leftrightarrow a = b\))
Lời giải chi tiết:
Khi \(\overrightarrow E \) hướng thẳng đứng xuống dưới, chu kì của con lắc là: \({T_1} = 2\pi \sqrt {\dfrac{{\rm{l}}}{{g + a}}} \)
Khi \(\overrightarrow E \) hướng theo phương ngang, chu kì của con lắc là: \({T_2} = \sqrt {\dfrac{{\rm{l}}}{{\sqrt {{g^2} + {a^2}} }}} \)
Ta có tỉ số: \(\dfrac{{{T_2}}}{{{T_1}}} = \sqrt {\dfrac{{g + a}}{{\sqrt {{g^2} + {a^2}} }}} \)
Áp dụng bất đẳng thức Cô – si, ta có:
\({g^2} + {a^2} \ge 2ga\) (dấu “=” xảy ra \( \Leftrightarrow g = a\))
\(\begin{array}{l} \Rightarrow 2\left( {{g^2} + {a^2}} \right) \ge {g^2} + {a^2} + 2ga \Rightarrow 2\left( {{g^2} + {a^2}} \right) \ge {\left( {g + a} \right)^2}\\ \Rightarrow \dfrac{{{{\left( {g + a} \right)}^2}}}{{{g^2} + {a^2}}} \le 2 \Rightarrow \sqrt {\dfrac{{g + a}}{{\sqrt {{g^2} + {a^2}} }}} \le \sqrt {\sqrt 2 } = 1,19\,\,\left( 1 \right)\end{array}\)
Lại có:
\(\begin{array}{l}g.a > 0\,\, \Rightarrow {g^2} + {a^2} + 2ga > {g^2} + {a^2}\\ \Rightarrow {\left( {g + a} \right)^2} > {g^2} + {a^2} \Rightarrow \sqrt {\dfrac{{g + a}}{{\sqrt {{g^2} + {a^2}} }}} > 1\,\,\left( 2 \right)\end{array}\)
Từ (1) và (2), ta có \(\dfrac{{{T_2}}}{{{T_1}}} = 1,15\) thỏa mãn
Chọn D.
Câu hỏi 40 :
Tại mặt đất có nhiệt độ \({25^0}C\), một con lắc đồng hồ có chu kỳ dao động nhỏ \(T = 2\,\,s\). Đưa con lắc lên độ cao \(6,5\,\,km\), nhiệt độ \({20^0}C\). Con lắc có hệ số nở dài \(\alpha = 1,{75.10^{ - 5}}\,\,{K^{ - 1}}\). Cho bán kính Trái Đất \(R = 6400\,\,km\). Hỏi sau một ngày đêm đồng hồ đó chạy
- A Chậm 80 s.
- B Nhanh 80 s
- C Chậm 84 s.
- D Nhanh 84 s.
Đáp án: D
Phương pháp giải:
Độ lệch thời gian của đồng hồ khi thay đổi nhiệt độ, độ cao: \(\dfrac{{\Delta T}}{T} = \dfrac{h}{R} + \dfrac{1}{2}\alpha \left( {{t_2} - {t_1}} \right)\)
Lời giải chi tiết:
Thời gian đồng hồ chạy sai sau 1 ngày đêm là:
\(\begin{array}{l}\Delta t = 86400.\dfrac{{\Delta T}}{T} = 86400\left[ {\dfrac{h}{R} + \dfrac{1}{2}\alpha \left( {{t_2} - {t_1}} \right)} \right]\\ \Rightarrow \Delta t = 86400\left[ {\dfrac{{6,5}}{{6400}} + \dfrac{1}{2}.1,{{75.10}^{ - 5}}.\left( {20 - 25} \right)} \right] = 83,97 \approx 84\,\,\left( s \right)\end{array}\)
Vậy sau 1 ngày đêm, đồng hồ chạy nhanh \(84\,\,s\)
Chọn D.