Câu hỏi 1 :
Con lắc đơn có chiều dài dây treo l, một đầu cố định và một đầu gắn vật nhỏ, dao động điều hoà tại nơi có gia tốc rơi tự do g. Tần số của dao động là:
- A
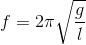
- B
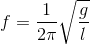
- C
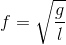
- D
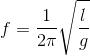
Đáp án: B
Phương pháp giải:
Phương pháp : Sử dụng công thức tính tần số của con lắc đơn dao động điều hoà
Lời giải chi tiết:
Đáp án B
Tần số của dao động của con lắc đơn là 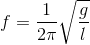
Câu hỏi 2 :
Chu kì dao động điều hoà của con lắc đơn phụ thuộc vào:
- A khối lượng của con lắc
- B biên độ dao động
- C năng lượng kích thích dao động
- D chiều dài của con lắc
Đáp án: D
Phương pháp giải:
Phương pháp: Sử dụng công thức tính chu kì dao động điều hoà của con lắc đơn để đánh gía
Lời giải chi tiết:
Đáp án D
\(T = 2\pi \sqrt {{l \over g}} \Rightarrow \) Chu kì dao động điều hoà của con lắc đơn phụ thuộc vào chiều dài của con lắc
Câu hỏi 3 :
Tại một nơi xác định, chu kì dao động điều hòa của con lắc đơn tỉ lệ thuận với
- A căn bậc hai chiều dài con lắc.
- B chiều dài con lắc.
- C căn bậc hai gia tốc trọng trường.
- D gia tốc trọng trường.
Đáp án: A
Phương pháp giải:
Phương pháp: Sử dụng công thức tính chu kì dao động điều hoà của con lắc đơn.
Lời giải chi tiết:
Đáp án A
Tại một nơi xác định, chu kì dao động điều hòa của con lắc đơn tỉ lệ thuận với căn bậc hai chiều dài con lắc
Câu hỏi 4 :
Tại nơi có gia tốc trọng trường g, một con lắc đơn dao động điều hòa với biên độ góc α0 nhỏ. Biết khối lượng vật nhỏ của con lắc là m, chiều dài dây treo là l, mốc thế năng ở vị trí cân bằng. Cơ năng của con lắc là;
- A 2mglα02
- B (1/2)mglα02
- C (1/4)mglα02
- D mglα02
Đáp án: B
Phương pháp giải:
Phương pháp: Sử dụng công thức tính cơ năng của con lắc đơn dao động điều hoà.
Lời giải chi tiết:
Đáp án B
W = (1/2)mglα02
Câu hỏi 5 :
Tại cùng một nơi trên Trái Đất, con lắc đơn có chiều dài ℓ dao động điều hòa với chu kì 2 s, con lắc đơn có chiều dài 2ℓ dao động điều hòa với chu kì là
- A 4 s.
- B \(2\sqrt 2 s\)
- C 2 s.
- D \(\sqrt 2 s\)
Đáp án: B
Phương pháp giải:
Sử dụng công thức tính chu kì dao động của con lắc đơn
Lời giải chi tiết:
Chu kì dao động của con lắc đơn dao động điều hoà: \(T = 2\pi \sqrt {{l \over g}} \Rightarrow T \sim \sqrt l \)
Theo đề bài: Con lắc đơn có chiều dài l dao động với chu kì 2s
→ Khi con lắc đơn có chiều dài l’ = 2l, nghĩa là tăng lên 2 lần → chu kì tăng \(\sqrt 2 \) lần.
Do đó \(T' = 2\sqrt 2 s\)
Câu hỏi 6 :
để đo gia tốc trọng trường dựa vào dao động của con lắc đơn, ta cần dụng cụ nào?
- A cân và thước
- B chỉ đồng hồ
- C đồng hồ và thước
- D chỉ thước
Đáp án: C
Lời giải chi tiết:
đáp án C
Câu hỏi 7 :
Cho con lắc đơn chiều dài l dao động nhỏ với chu kỳ T. Nếu tăng khối lượng vật treo gấp 4 lần thì chu kỳ con lắc
- A Tăng lên 4 lần.
- B Tăng lên 8 lần.
- C Tăng lên 2 lần.
- D Không thay đổi.
Đáp án: D
Lời giải chi tiết:
Câu hỏi 8 :
Một con lắc đơn dao động điều hòa với tần số góc 4 rad/s tại một nơi có gia tốc trọng trường 10 m/s2. Chiều dài dây treo của con lắc là
- A 50 cm.
- B 62,5 cm.
- C 125 cm.
- D 81,5 cm.
Đáp án: B
Lời giải chi tiết:
Câu hỏi 9 :
Một con lắc đơn đang dao động điều hòa trong mặt phẳng thẳng đứng, biết vật nặng tích điện q. Đúng lúc nó đến vị trí có góc lệch cực đại thì thiết lập một điện trường đều có đường sức thẳng đứng. Sau đó vật tiếp tục dao động với:
- A biên độ như cũ.
- B chu kì như cũ.
- C vận tốc cực đại như cũ.
- D cơ năng như cũ.
Đáp án: A
Lời giải chi tiết:
Đáp án A
+ Tại vị trí biên v = 0, thiết lập điện trường → vị trí cân bằng ko thay đổi → biên độ dao động không đổi.
Câu hỏi 10 :
Tại một nơi có gia tốc trọng trường g = 9,8 m/s2, một con lắc đơn có chiều dài dây treo l = 1,0 m, đang dao động điều hòa trên một đoạn quỹ đạo có độ dài 10 cm. Biên độ góc của dao động là
- A 0,1 rad.
- B 0,05 rad.
- C 50.
- D 100.
Đáp án: B
Lời giải chi tiết:
Đáp án B
+ Biên độ góc $${\alpha _0} = {{{s_0}} \over l} = 0,05\,rad$$
Câu hỏi 11 :
Khi đưa một con lắc đơn lên cao theo phương thẳng đứng (coi chiều dài của con lắc không đỏi) thì tần số dao động điều hòa với biên độ nhỏ của con lắc sẽ
- A tăng vì gia tốc trọng trường tăng theo chiều cao.
- B giảm vì gia tốc trọng trường giảm theo chiều cao.
- C giảm vì gia tốc trọng trường giảm theo chiều cao.
- D tăng vì gia tốc trọng trường giảm theo chiều cao.
Đáp án: B
Phương pháp giải:
Sử dụng công thức tính tần số của con lắc đơn để đánh giá
Lời giải chi tiết:
Ta có: \(f = {\omega \over {2\pi }} = {1 \over {2\pi }}\sqrt {{g \over l}} \)
Khi đưa con lắc đơn lên cao thì gia tốc trọng trường giảm => tần số giảm.
Chọn B
Câu hỏi 12 :
Một con lắc đơn có chiều dài l = 1 m treo ở trần một thang máy, khi thang máy đi xuống nhanh dần đều với gia tốc a =g/2 (g = π2 m/s2) thì chu kì dao động bé của con lắc là
- A 4 s.
- B 2,83 s.
- C 1,64 s.
- D 2 s.
Đáp án: B
Phương pháp giải:
Con lắc đơn dao động trong thang máy
Lời giải chi tiết:
Đáp án B
+ Thang máy đi xuống nhanh dần đều → gbk = g – a = 0,5g.
→ Chu kì dao động của con lắc $$T = 2\pi \sqrt {{l \over {{g_{bk}}}}} = 2,83 s$$.
Câu hỏi 13 :
Con lắc đơn có chiều dài 1 m, dao động điều hòa với tần số 0,5 Hz. Lấy π = 3,14. Gia tốc trọng trường tại nơi treo con lắc là:
- A 9,78 m/s2.
- B 10 m/s2.
- C 9,86 m/s2.
- D 9,80 m/s2.
Đáp án: C
Phương pháp giải:
Phương pháp: công thức tính tần số của con lắc đơn $$f = {1 \over {2\pi }}\sqrt {{g \over l}} $$
Lời giải chi tiết:
Đáp án C
Ta có $$f = {1 \over {2\pi }}\sqrt {{g \over l}} = > g = 9,86\,m/{s^2}$$
Câu hỏi 14 :
Trong quá trình dao động điều hòa của con lắc đơn. Nhận định nào sau đây sai?
- A Khi quả nặng ở điểm giới hạn, lực căng dây treo có độ lớn nhỏ hơn trọng lượng của vật
- B Độ lớn của lực căng dây treo con lắc luôn lớn hơn trọng lượng vật
- C Chu kỳ dao động của con lắc không phụ thuộc vào biên độ dao động của nó
- D Khi góc hợp bởi phương dây treo còn lắc và phương thẳng đứng giảm, tốc độ của quả nặng sẽ tăng
Đáp án: B
Lời giải chi tiết:
Đáp án B
+ Trong quá trình dao động điều hóa của con lắc đơn, tại vị trí biên thì lực căng dây nhỏ hơn trọng lượng của vật.
Câu hỏi 15 :
Một con lắc đơn có chiều dài dây treo 50cm và vật nhỏ có khối lượng 10g mang điện tích q=+6.10.-6 C, được coi là điện tích điểm. Con lắc dao động điều hòa trong điện trường đều mà vecto cường độ điện trường có độ lớn E=104V/m và hướng thẳng đứng xuống dưới. Lấy g=10m/s2, π=3,14. Chu kì dao động điều hòa của con lắc là
- A 0,58 s.
- B 1,40 s.
- C 1,99 s.
- D 1,11 s.
Đáp án: D
Phương pháp giải:
Con lắc đơn chịu thêm tác dụng của lực điện
Lực điện : Fđ = qE
Lời giải chi tiết:
q > 0 ; \(\overrightarrow E \) hướng thẳng đứng xuống dưới \( \Rightarrow \overrightarrow {{F_d}} \uparrow \uparrow \overrightarrow P \)
=> Chu kì dao động điều hoà của con lắc :\(T = 2\pi \sqrt {{l \over {g + {{qE} \over m}}}} = 2.3,14.\sqrt {{{0,5} \over {10 + {{{{6.10}^{ - 6}}{{.10}^4}} \over {{{10.10}^{ - 3}}}}}}} = 1,11s\)
Chọn D
Câu hỏi 16 :
Chu kỳ dao động điều hòa của con lắc đơn có chiều dài l, tại nơi có gia tốc trọng trường g,được xác định bởi công thức nào sau đấy?
- A \(T = 2\pi \sqrt {\frac{g}{l}} \)
- B \(T = 2\pi \sqrt {\frac{l}{g}} \)
- C \(T = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \)
- D \(T = \frac{1}{{2\pi }}\sqrt {\frac{l}{g}} \)
Đáp án: B
Lời giải chi tiết:
Đáp án B
Câu hỏi 17 :
Một con lắc đơn, quả nặng có khối lượng 40 g dao động nhỏ với chu kỳ 2s . Nếu gắn thêm một gia trọng có khối lượng 120 g thì con lắc sẽ dao động nhỏ với chu kỳ
- A 4 s
- B 0,25s
- C \(2\sqrt 3 s\)
- D 2s
Đáp án: D
Lời giải chi tiết:
Đáp án D
Chu kỳ của con lắc đơn không phụ thuộc vào khối lượng của quả nặng
Câu hỏi 18 :
Một con lắc đơn có dây treo vật là một sợi dây kim lại nhẹ thẳng nhẹ dài 1m, dao động điều hòa vời biên độ góc 0,2 rad trong một từ trường đều mà cảm ứng từ có hướng vuông góc với mặt phẳng dao động của con lắc và có độ lớn 1T. Lấy g = 10 m/s2. Suất điện động cực đại xuất hiện trên dây treo con lắc có giá trị là
- A 0,63 V
- B 0,22 V
- C 0,32 V
- D 0,45 V
Đáp án: A
Phương pháp giải:
Phương pháp : Áp dụng công thức tính suất điện động cảm ứng \(\zeta = \omega BS\)
Lời giải chi tiết:
Đáp án A
Ta có hình vẽ
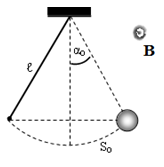
Diện tích mà con lắc quét được trong quá trình dao động là \(S = \frac{{\pi .{R^2}.2{\alpha _0}}}{{360}} = \frac{{\pi .{R^2}.2.180.0,4}}{{360.\pi }} = 0,2{m^2}\)
Suất điện động cực đại xuất hiện trên dây treo của con lắc là \(\zeta = \omega .B.S = \sqrt {\frac{g}{l}} .1.0,2 = 0,63V\)
Câu hỏi 19 :
Khi con lắc đơn dao động với phương trình \(s = 5\cos 10\pi t(mm)\) thì thế năng của nó biến thiên với tần số
- A 5 Hz
- B 2,5 Hz
- C 10 Hz
- D 20 Hz
Đáp án: D
Lời giải chi tiết:
Đáp án D
Trong dao động điều hòa của con lắc đơn thế năng biến thiên với tần số bằng 2 lần tần số của li độ
Câu hỏi 20 :
Có ba con lắc cùng chiều dài dây treo, cùng khối lượng vật nặng. Con lắc thứ nhất và con lắc thứ hai mang điện tích q1 và q2, con lắc thức ba không mang điện tích. Chu kì dao động điều hoà của chúng trong điện trường đều có phương thẳng đứng lần lượt là T1; T2 và T3 với với T1 = T3/3; T2 = 2T3/3. Tỉ số điện tích q1/q2 bằng
- A 4,6
- B 3,2
- C 2,3
- D 6,4
Đáp án: D
Phương pháp giải:
Phương pháp: Chu kì của con lắc đơn chịu thêm tác dụng của lực điện trường
Lời giải chi tiết:
Đáp án D
Cách giải:
Chu kì dao động của con lắc thứ 3: \({T_3} = 2\pi \sqrt {\frac{l}{g}} \)
Có T1 = T3/3 => T3 = 3T1 => T3> T1 \( \Rightarrow {T_1} = 2\pi \sqrt {\frac{l}{{g + \frac{{{q_1}E}}{m}}}} \)
Có T2 = 2T3/3 => T3> T2\( \Rightarrow {T_2} = 2\pi \sqrt {\frac{l}{{g + \frac{{{q_2}E}}{m}}}} \)
Ta có:
\(\left\{ \matrix{
{T_1} = {{{T_3}} \over 3} \hfill \cr
{T_2} = 2{{{T_3}} \over 3} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{1 \over {\sqrt {g + {{{q_1}E} \over m}} }} = {1 \over 3}{1 \over {\sqrt g }} \hfill \cr
{1 \over {\sqrt {g + {{{q_2}E} \over m}} }} = {2 \over 3}{1 \over {\sqrt g }} \hfill \cr} \right. \Rightarrow g = {{{q_1}E} \over {8m}} \Rightarrow {{{q_1}} \over {{q_2}}} = 6,4\)
Câu hỏi 21 :
Một con lắc đơn có chiều dài dây treo 50 cm., đang dao động điều hòa với biên độ góc 0,08 rad. Biên độ dài của của vật dao động là
- A 8 cm
- B 6 cm
- C 6 cm
- D 4 cm
Đáp án: D
Lời giải chi tiết:
Đáp án D
Biên độ dài của vật dao động là\({S_0} = l.{\alpha _0} = 50.0,08 = 4cm\)
Câu hỏi 22 :
Một con lắc đơn dao động điều hoà. Nếu tăng khối lượng của quả nặng hai lần và giữ nguyên biên độ dao động thì
- A chu kì giảm 2 lần, cơ năng không đổi
- B chu kì không đổi, cơ năng tăng 2 lần
- C chu kì và cơ năng của con lắc có giá trị không đổi
- D chu kì tăng 2 lần, cơ năng tăng 2 lần
Đáp án: B
Phương pháp giải:
Phương pháp: Sử dụng công thức tính chu kì dao động và cơ năng của con lắc đơn
Lời giải chi tiết:
Đáp án B
Cách giải:
Ta có:
\(\left\{ \matrix{
T = 2\pi \sqrt {{l \over g}} \hfill \cr
{\rm{W}} = {{mgl\alpha _0^2} \over 2} \hfill \cr} \right.\)
Khi tăng khối lượng của quả nặng hai lần => Chu kì T không đổi, cơ năng tăng 2 lần
Câu hỏi 23 :
Một con lắc đơn gồm một viên bi nhỏ khối lượng m treo ở đầu một sợi dây nhẹ, không co dãn dao động nhỏ tại nơi có gia tốc trọng trường g với chu kì T0. Nếu tích điện q > 0 cho viên bi và đặt con lắc đơn đó trong một điện trường đều có véctơ cường độ điện trường $\overrightarrow E $ hướng thẳng đứng xuống dưới sao cho qE = 8mg thì chu kì T của con lắc lúc này là:
- A $T = \frac{{{T_0}}}{9}$
- B T = 8T0
- C $T = \frac{{{T_0}}}{3}$
- D T = 3T0
Đáp án: C
Phương pháp giải:
Phương pháp: Chu kì của con lắc đơn chịu thêm tác dụng của lực điện
Lời giải chi tiết:
Đáp án C
Cách giải:
+ Khi chưa tích điện cho viên bi: \({T_0} = 2\pi \sqrt {\frac{l}{g}} \)
+ Khi tích điện q > 0 cho quả cầu:
Ta có: \(\overrightarrow {{F_d}} = q\overrightarrow E ;q > 0 \Rightarrow \overrightarrow {{F_d}} \uparrow \uparrow \overrightarrow E \)
\(\overrightarrow E $$ hướng thẳng đứng xuống dưới => $$\overrightarrow {{F_d}} $$ hướng thẳng đứng xuống dưới
=> Chu kì: \({T_0} = 2\pi \sqrt {\frac{l}{{g + \frac{{qE}}{m}}}} = 2\pi \sqrt {\frac{l}{{g + \frac{{8mg}}{m}}}} = 2\pi \sqrt {\frac{l}{{9g}}} = \frac{1}{3}.2\pi \sqrt {\frac{l}{g}} = \frac{{{T_0}}}{3}\)
Câu hỏi 24 :
Hai con lắc đơn có chiều dài lần lượt là 81cm và 64cm được treo ở trần một căn phòng. Khi các vật nhỏ của hai con lắc đang ở vị trí cân bằng, đồng thời truyền cho chúng các vận tốc cùng hướng sao cho hai con lắc dao động điều hoà với cùng biên độ góc, trong hai mặt phẳng song song với nhau.Giá trị ∆t gần giá trị nào nhất sau đây?
- A 2,36s
- B 7,20s
- C 0,45s
- D 8,12s
Đáp án: C
Phương pháp giải:
Phương pháp : Áp dụng công thức tính tần số góc của con lắc đơn
Lời giải chi tiết:
Đáp án C
Cách giải:
Áp dụng công thức tính tần số góc của con lắc đơn ta có
\({\omega _1} = \sqrt {\frac{g}{{{l_1}}}} = \sqrt {\frac{{10}}{{0,91}}} = \frac{{\sqrt {10} }}{{0,9}};{\omega _2} = \sqrt {\frac{g}{{{l_2}}}} = \sqrt {\frac{{10}}{{0,64}}} = \frac{{\sqrt {10} }}{{0,8}}\)
Ta có phương trình dao động của hai con lắc: \({a_1} = {a_0}cos({\omega _1}t - \frac{\pi }{2});a = {a_0}cos({\omega _2}t - \frac{\pi }{2})\)
Hai dây treo song song nhau lần đầu khi pha của hai dao động đối nhau:
\(\eqalign{
& ({\omega _1}t - {\pi \over 2}) = - ({\omega _2}t - {\pi \over 2}) \cr
& \Rightarrow \Delta t = t = {\pi \over {{\omega _1} + {\omega _2}}}\Delta t = {{\pi .0,9.0,8} \over {\sqrt {10} .(0,9 + 0,8)}} = 0,42s \cr} \)
Câu hỏi 25 :
Một con lắc đơn có chu kì T = 1s trong vùng không có điện trường, quả lắc có khối lượng m = 10g bằng kim loại mang điện tích q = 10-5C. Con lắc được đem treo trong điện trường đều giữa hai bản kim loại phẳng song song mang điện tích trái dấu, đặt thẳng đứng, hiệu điện thế giữa hai bản bằng 400V. Kích thước các bản kim loại rất lớn so với khoảng cách giữa chúng. Cho khoảng cách giữa hai bản d = 10cm. Tìm chu kì con lắc khi dao động trong điện trường giữa hai bản kim loại đó?
- A 0,694s
- B 0,928s
- C 0,631s
- D 0,580s
Đáp án: A
Phương pháp giải:
Phương pháp: Sử dụng lí thuyết về con lắc đơn chịu thêm tác của lực điện
Lời giải chi tiết:
Đáp án A
Cách giải:
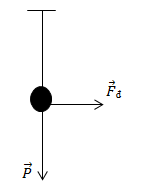
- Khi không có điện trường: \(T = 2\pi \sqrt {\frac{l}{g}} \)
- Khi con lắc được treo trong điện trường: \(T' = 2\pi \sqrt {\frac{l}{{g'}}} = 2\pi \sqrt {\frac{l}{{\sqrt {{g^2} + {a^2}} }}} \)
Với: + Cường độ điện trường: \(E = \frac{U}{d} = \frac{{400}}{{{{10.10}^{ - 2}}}} = 4000(V/m)\)
+ \(a = \frac{{\left| q \right|E}}{m} = \frac{{{{10}^{ - 5}}.4000}}{{{{10.10}^{ - 3}}}} = 4\left( {m/{s^2}} \right)\)
\( \Rightarrow \frac{{T'}}{T} = \sqrt {\frac{g}{{\sqrt {{g^2} + {a^2}} }}} \Leftrightarrow T' = \sqrt {\frac{{10}}{{\sqrt {{{10}^2} + {4^2}} }}} = 0,964s\)
Câu hỏi 26 :
Một con lắc đơn gồm vật nhỏ khối lượng m gắn vào đầu dưới của một dây treo không dãn có chiều dài l. Kích thích cho con lắc đơn dao động điều hoà tại nơi có gia tốc trọng trường g thì chu kì dao động của nó được xác định bởi công thức
- A \(T = 2\pi \sqrt {{l \over g}} \)
- B \(T = {1 \over {2\pi }}\sqrt {{g \over l}} \)
- C \(T = {1 \over {2\pi }}\sqrt {{g \over m}} \)
- D \(T = 2\pi \sqrt {{m \over g}} \)
Đáp án: A
Lời giải chi tiết:
Chu kì dao động của con lắc đơn \(T = 2\pi \sqrt {{l \over g}} \)
Câu hỏi 27 :
Vật nhỏ của một con lắc đơn có khối lượng 200g dao động điều hòa tại nơi có gia tốc trọng trường 9,8 m/s2 . Khi vật nhỏ đi qua vị trí có li độ góc là 40 thì lực kéo về có độ lớn
- A 6,28 N
- B 0,137 N
- C 7,846 N
- D 0,257 N
Đáp án: B
Lời giải chi tiết:
Đáp án B
Phương pháp giải: Sử dụng công thức tính lực kéo về của con lắc đơn dao động điều hòa
Đổi \(\alpha = {4^0} = \frac{\pi }{{45}}\,rad\)
\(F = m{\omega ^2}s = m{\omega ^2}\alpha l = m\frac{g}{l}.\frac{\pi }{{45}}.l = 0,137N\)
Câu hỏi 28 :
Một con lắc đơn dài l = 1m dao động điều hoà tại một nơi có gia tốc trọng trường g = 10m/s2 với biên độ 10cm. Lấy π2 =10. Khi quả cầu ở vị trí có li độ góc α =40 thì tốc độ của quả cầu là
- A 22,5cm/s
- B 25,1cm/s
- C 19,5cm/s
- D 28,9cm/s
Đáp án: A
Phương pháp giải:
áp dụng định luật bảo toàn cơ năng
Lời giải chi tiết:
Góc lệch cực đại của con lắc là:
\({\alpha _0} = \frac{s}{l} = \frac{{10}}{{100}} = 0,1rad = {5^0}43'\)
Chọn mốc tính thế năng ở vị trí cân bằng, ta áp dụng định luật bảo toàn cơ năng:
\[\begin{gathered}
{{\text{W}}_d} + {{\text{W}}_t} = {{\text{W}}_{t\max }} \Leftrightarrow \frac{1}{2}.m.{v^2} + mg.l.\left( {1 - \cos \alpha } \right) = mgl.\left( {1 - \cos {\alpha _0}} \right) \hfill \\
\Leftrightarrow v = \sqrt {2gl.\left( {\cos \alpha - \cos {\alpha _0}} \right)} = \sqrt {2.10.1.\left( {\cos {4^0} - \cos {5^0}43'} \right)} = 0,225m/s = 22,5cm/s \hfill \\
\end{gathered} \]
Câu hỏi 29 :
Tại một phòng thí nghiệm, học sinh A sử dụng con lắc đơn để đo gia tốc rơi tự do g bằng phép đo gián tiếp. Kết quả đo chu kì và chiều dài của con lắc đơn là $T = 1,919 \pm 0,001(s)$ và $l = 0,9 \pm 0,002(m)$. Bỏ qua sai số của số pi. Cách viết kết quả đo nào sau đây là đúng?
- A $g = 9,648 \pm 0,031m/{s^2}$
- B $g = 9,544 \pm 0,035m/{s^2}$
- C $g = 9,648 \pm 0,003m/{s^2}$
- D $g = 9,544 \pm 0,003m/{s^2}$
Đáp án: A
Phương pháp giải:
Phương pháp : Sử dụng công thức tính chu kì dao động của con lắc đơn và công thức tính sai số trong thực hành thí nghiệm
Lời giải chi tiết:
Đáp án A
Cách giải :
Công thức xác định độ lớn gia tốc trọng trường: $g = \frac{{4{\pi ^2}\ell }}{{{T^2}}} = \frac{{4{\pi ^2}\ell .0,9}}{{1,{{919}^2}}} = 9,648$
Ta có:$g = \frac{{4{\pi ^2}\ell }}{{{T^2}}} \to \ln g = \ln 4{\pi ^2} + \ln \ell - \ln {T^2} \to \frac{{\Delta g}}{g} = \frac{{\Delta \ell }}{\ell } + 2\frac{{\Delta T}}{T} \to \Delta g = g\left( {\frac{{\Delta \ell }}{\ell } + 2\frac{{\Delta T}}{T}} \right) = 0,031$
Câu hỏi 30 :
Tại một nơi trên mặt đất, một con lắc đơn dao động điều hòa. Trong khoảng thời gian ∆t, con lắc thực hiện 60 dao động toàn phần; thay đổi chiều dài con lắc một đoạn 44 cm thì cũng trong khoảng thời gian ∆t ấy, nó thực hiện 50 dao động toàn phần. Chiều dài ban đầu của con lắc là
- A 144 cm.
- B 60 cm.
- C 80 cm.
- D 100 cm.
Đáp án: D
Phương pháp giải:
Phương pháp : Áp dụng công thức tính chu kỳ dao động của con lắc đơn $T = 2\pi \sqrt {\frac{l}{g}} $
Lời giải chi tiết:
Đáp án D
Cách giải:
Trong khoảng thời gian ∆t, con lắc thực hiện 60 dao động toàn phần; thay đổi chiều dài con lắc một đoạn 44 cm thì cũng trong khoảng thời gian ∆t ấy, nó thực hiện 50 dao động toàn phần. Chiều dài ban đầu của con lắc là
$\eqalign{
& 60.T = 60.2\pi \sqrt {{l \over g}} ;50.T = 50.2\pi \sqrt {{{l + 0,44} \over g}} \cr
& \Rightarrow 60.2\pi \sqrt {{l \over g}} = 50.2\pi \sqrt {{{l + 0,44} \over g}} \Rightarrow {6 \over 5} = \sqrt {{{l + 0,44} \over l}} \Rightarrow {{36} \over {25}} = {{l + 0,44} \over l} \Rightarrow l = 100cm \cr} $
Câu hỏi 31 :
Một con lắc đơn dao động điều hòa. Nếu tăng khối lượng của quả nặng hai lần giữ nguyên biên độ và vị trí, môi trường dao động thì so với khi chưa tăng khối lượng.
- A chu kì giảm 2 lần, cơ năng không đổi
- B chu kì tăng 2 lần, cơ năng tăng 2 lần
- C chu kì không đổi, cơ năng tăng 2 lần
- D chu kì và cơ năng của con lắc có giá trị không đổi
Đáp án: C
Lời giải chi tiết:
+ Chu kì con lắc đơn không phụ thuộc vào khối lượng vật nặng → T không đổi
+ Năng lượng E tỉ lệ với m → E tăng 2 lần khi m tăng 2 lần.
Câu hỏi 32 :
Tại nơi có gia tốc trọng trường g, một con lắc đơn dao động điều hòa với biên độ góc a0. Biết khối lượng vật nhỏ của con lắc là m, chiều dài dây treo là , mốc thế năng ở vị trí cân bằng. Cơ năng của con lắc là
- A 1/4mglα02.
- B 2mglα02.
- C mglα02
- D 1/2mglα02.
Đáp án: D
Phương pháp giải:
Cơ năng của con lắc \(\frac{1}{2}mg\ell \alpha _{0}^{2}\)
Lời giải chi tiết:
Cơ năng của con lắc \(\frac{1}{2}mg\ell \alpha _{0}^{2}\)
Câu hỏi 33 :
Tại cùng một nơi trên mặt đất, nếu tần số dao động điều hoà của con lắc đơn chiều dài ℓ = 1m, g = π2m/s2 thì chu kì dao động điều hoà của con lắc đơn là:
- A 4s
- B 2s
- C 8s
- D 1s
Đáp án: B
Phương pháp giải:
chu kỳ dao động của con lắc đơn \(T=2\pi \sqrt{\frac{\ell }{g}}\0
Lời giải chi tiết:
Chu kỳ dao động của con lắc:
\(T=2\pi \sqrt{\frac{\ell }{g}}=2\pi \sqrt{\frac{1}{{{\pi }^{2}}}}=2s\)
Câu hỏi 34 :
Phát biểu nào sau đây là sai khi nói về dao động của con lắc đơn (bỏ qua lực cản của môi trường)?
- A Khi vật nặng ở vị trí biên, cơ năng của con lắc bằng thế năng của nó
- B Khi vật nặng đi qua vị trí cân bằng, thì lực căng dây bằng không
- C Với biên độ góc nhỏ thì dao động của con lắc là dao động điều hòa
- D Chuyển động của con lắc từ vị trí biên về vị trí cân bằng là nhanh dần
Đáp án: B
Phương pháp giải:
Với con lắc đơn dao động điều hòa
- Cơ năng bằng động năng cực đại và bằng thế năng cực đại.
- Lực căng dây T = 3mg(cosα – cosα0)
- Tại biên độ lớn li độ cực đại, tốc độ bằng 0, tại VTCB li độ bằng 0 còn tốc độ cực đại
Lời giải chi tiết:
Khi vật nặng đi qua vị trí cân bằng, thì lực căng dây T = 3mg(cos0 – cosα0) = 3mg(1 – cosα0)
Câu hỏi 35 :
Một con lắc đơn gồm một sợi dây dài l khối lượng không đáng kể, không co dãn và một hòn bi có khối lượng m. Khi con lắc dao động điều hòa tại nơi có gia tốc trọng trường g thì tần số dao động của con lắc là
- A \(f=2\pi \sqrt{\frac{g}{l}}\)
- B \(f=2\pi \sqrt{\frac{l}{g}}\)
- C \(f=\frac{1}{2\pi }\sqrt{\frac{g}{l}}\)
- D \(f=\frac{1}{2\pi }\sqrt{\frac{l}{g}}\)
Đáp án: C
Phương pháp giải:
Tần số dao động của con lắc đơn: \(f=\frac{1}{2\pi }\sqrt{\frac{g}{l}}\)
Lời giải chi tiết:
Tần số dao động của con lắc đơn: \(f=\frac{1}{2\pi }\sqrt{\frac{g}{l}}\)
Chọn C
Câu hỏi 36 :
Đồ thị biểu diễn chu kỳ dao động bé của con lắc đơn theo chiều dài dây treo là đường
- A hypebol
- B parabol
- C elip
- D thẳng bậc nhất
Đáp án: B
Phương pháp giải:
Chu kỳ dao động nhỏ của con lắc đơn: \(T=2\pi \sqrt{\frac{\ell }{g}}\)
Lời giải chi tiết:
Chu kỳ dao động nhỏ của con lắc đơn: \(T=2\pi \sqrt{\frac{\ell }{g}}\Rightarrow {{T}^{2}}\tilde{\ }\ell \)
Vậy đồ thị biểu diễn chu kỳ dao động bé của con lắc đơn theo chiều dài dây treo là đường parabol
Chọn B
Câu hỏi 37 :
Ứng dụng quan trọng nhất của con lắc đơn là
- A xác định chiều dài con lắc
- B xác định gia tốc trọng trường
- C xác định chu kì dao động
- D khảo sát dao động điềuhòa của một vật
Đáp án: B
Phương pháp giải:
Ứng dụng quan trọng nhất của con lắc đơn là: xác định gia tốc trọng trường
Lời giải chi tiết:
Ứng dụng quan trọng nhất của con lắc đơn là: xác định gia tốc trọng trường.
Chọn B
Câu hỏi 38 :
Một con lắc đơn có dây treo dài 1 m. Kéo con lắc lệch khỏi vị trí cân bằng một góc 600 rồi thả nhẹ. Bỏ qua ma sát, lấy g = 10 m/s2. Vận tốc của vật khi nó qua vị trí cân bằng có độ lớn bằng bao nhiêu ?
- A 10 m/s
- B 3,16 cm/s
- C 1,58 m/s
- D 3,16 m/s
Đáp án: D
Phương pháp giải:
Áp dụng công thức tính vận tốc của con lắc đơn khi qua vị trí cân bằng:
\({{\text{v}}_{\text{max}}}=\sqrt{\text{2gl(1}-\text{cos}{{\text{ }\!\!\alpha\!\!\text{ }}_{\text{max}}}\text{)}}\)
Lời giải chi tiết:
Ta có: \({{\text{v}}_{\text{max}}}=\sqrt{\text{2gl(1}-\text{cos}{{\text{ }\!\!\alpha\!\!\text{ }}_{\text{max}}}\text{)}}=\sqrt{10}\approx \text{3,16 (m/s)}\)
Chọn D
Câu hỏi 39 :
Một con lắc đơn gồm vật nhỏ và sợi dây có chiều dài l đặt tại nơi có gia tốc trọng trường g. Khi dao động nhỏ, con lắc dao động điều hòa với chu kỳ
- A \(\frac{1}{2\pi }\sqrt{\frac{g}{l}}\)
- B \(\frac{1}{2\pi }\sqrt{\frac{l}{g}}\)
- C \(2\pi \sqrt{\frac{l}{g}}\)
- D \(2\pi \sqrt{\frac{g}{l}}\)
Đáp án: C
Phương pháp giải:
Một con lắc đơn gồm vật nhỏ và sợi dây có chiều dài l đặt tại nơi có gia tốc trọng trường g. Khi dao động nhỏ, con lắc dao động điều hòa với chu kỳ:
\(2\pi \sqrt{\frac{l}{g}}\)
Lời giải chi tiết:
Một con lắc đơn gồm vật nhỏ và sợi dây có chiều dài l đặt tại nơi có gia tốc trọng trường g. Khi dao động nhỏ, con lắc dao động điều hòa với chu kỳ:
\(2\pi \sqrt{\frac{l}{g}}\)
Chọn C
Câu hỏi 40 :
Con lắc đơn gồm vật nhỏ nặng 90g treo vào sợi dây nhẹ không giãn dài 30 cm và dao động điều hòa với biên độ góc 80. Cơ năng của con lắc này xấp xỉ bằng
- A 2,63 mJ
- B 10,53 mJ
- C 5,26 mJ
- D 37,70 mJ
Đáp án: A
Phương pháp giải:
Sử dụng công thức tính cơ năng của con lắc đơn
Lời giải chi tiết:
Sử dụng công thức tính cơ năng của con lắc đơn:
\(\text{W = }\frac{\text{mgl}}{\text{2}}\text{ }\!\!\alpha\!\!\text{ }_{\text{max}}^{\text{2}}\text{= 2,63}\text{.1}{{\text{0}}^{\text{-3}}}\text{(J)}\)