4. Bài 8. Chuyển động biến đổi. Gia tốc

8.1

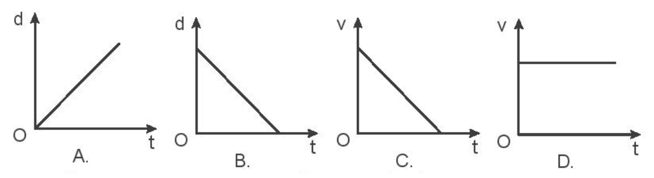
Đồ thị nào sau đây là của chuyển động biến đổi?

Phương pháp giải:

Vận dụng khái niệm, đặc điểm của chuyển động biến đổi để suy ra dạng đồ thị của nó.

Lời giải chi tiết:

A, B là chuyển động thẳng đều có độ dịch chuyển tỉ lệ thuận với thời gian chuyển động t.

C là chuyển động biến đổi vì có vận tốc thay đổi theo thời gian.

D là chuyển động thẳng đều vì có vận tốc không đổi theo thời gian.

Chọn đáp án C

8.2

Chuyển động nào sau đây là chuyển động biến đổi?

A. Chuyển động có độ dịch chuyển tăng đều theo thời gian.

B. Chuyển động có độ dịch chuyển giảm đều theo thời gian.

C. Chuyển động có độ dịch chuyển không đổi theo thời gian.

D. Chuyển động tròn đều.

Phương pháp giải:

Vận dụng lý thuyết về chuyển động biến đổi.

Lời giải chi tiết:

A, B sai vì chuyển động có độ dịch chuyển tăng đều hoặc giảm đều theo thời gian là chuyển động đều.

C sai vì chuyển động có độ dịch chuyển không đổi theo thời gian thì vật đang ở trạng thái đứng yên.

D đúng vì chuyển động tròn đều vận tốc tuy có độ lớn không đổi nhưng hướng luôn thay đổi nên chuyển động này có gia tốc và cũng là chuyển động biến đổi.

Chọn đáp án D.

8.3

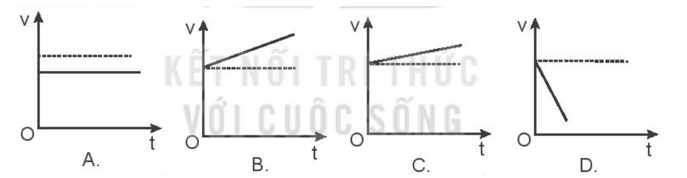
Đồ thị vận tốc thời gian nào sau đây mô tả chuyển động có độ lớn của gia tốc là lớn nhất?

Phương pháp giải:

Vận dụng công thức tính độ lớn của gia tốc để xác định: a = \(\frac{{\Delta v}}{{\Delta t}}\).

Lời giải chi tiết:

Độ lớn của gia tốc được xác định bằng độ biến thiên của vận tốc trong thời gian ∆t:  a = \(\frac{{\Delta v}}{{\Delta t}}\).

Vì vậy độ lớn của gia tốc tỉ lệ thuận với độ biến thiên vận tốc. Tức là độ biến thiên vận tốc càng lớn thì gia tốc càng lớn và ngược lại.

Quan sát lần lượt các đồ thị ta thấy đồ thị D vận tốc có độ biến thiên lớn nhất.

Chọn đáp án D.

8.4

Một người lái xe tải đang cho xe chạy trên đường cao tốc với vận tốc không đổi. Khi thấy khoảng cách giữa xe mình với xe chạy phía trước giảm dần, người đó cho xe chạy chậm dần. Tới khi thấy khoảng cách này đột nhiên giảm nhanh, người đó vội đạp phanh để dừng xe. Hãy vẽ đồ thị vận tốc - thời gian mô tả trạng thái chuyển động của xe tải trên.

Phương pháp giải:

Xác định các loại chuyển động trong từng chuyển động và biểu diễn tương ứng trên đồ thị.

Lời giải chi tiết:

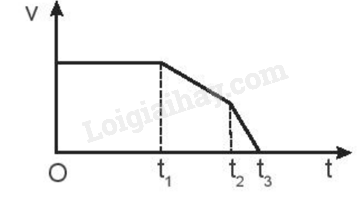
- Thời điểm ban đầu đến khi thấy khoảng cách giữa xe mình với xe chạy phía trước giảm dần (t₁) xe chạy với vận tốc không đổi => đồ thị vận tốc – thời gian là đường thẳng.

- Từ thời điểm t₁ đến trước khi thấy khoảng cách này đột nhiên giảm nhanh (t₂) xe chạy chậm dần => Đồ thị vận tốc – thời gian dốc xuống.

- Từ thời điểm t₂ đến khi xe dừng hẳn (t₄) vận tốc giảm nhanh xuống 0 => đồ thị vận tốc – thời gian dốc mạnh xuống và kết thúc tại vị trí có vận tốc bằng 0. Từ các dữ kiện trên ta vẽ được đồ thị vận tốc - thời gian có hình dạng như sau:

8.5

Một chiếc ô tô đang chạy với vận tốc 23 m/s thì chạy chậm dần. Sau 10 s, vận tốc của ô tô chỉ còn 11 m/s Tính gia tốc của ô tô. Gia tốc này có gì đặc biệt?

Phương pháp giải:

Áp dụng công thức tính gia tốc: a = \(\frac{{\Delta v}}{{\Delta t}}\).

Lời giải chi tiết:

Gia tốc của ô tô: a = \(\frac{{\Delta v}}{{\Delta t}}\)= \(\frac{{{v_s} - {v_t}}}{{\Delta t}}\)=\(\frac{{11 - 23}}{{10}}\)= -1,2 m/s²

Gia tốc này âm vì ô tô chuyển động chậm dần.

8.6

Một quả bóng tennis đang bay với vận tốc 25 m/s theo hướng đông thì chạm vào tường chắn và bay trở lại với vận tốc 15 m/s theo hướng tây. Thời gian và chạm giữa tường và bóng là 0,05 s.

a) Tính sự thay đổi tốc độ của quả bóng.

b) Tính sự thay đổi vận tốc của quả bóng.

c) Tính gia tốc của quả bóng trong thời gian tiếp xúc với tường.

Phương pháp giải:

- Tính sự thay đổi tốc độ bằng cách lấy tốc độ lớn hơn – tốc độ nhỏ hơn: \(\Delta \upsilon  = {\upsilon _l} - {\upsilon _n}\)

- Tính sự thay đổi vận tốc bằng cách lấy vận tốc lúc sau – vận tốc lúc trước:

∆v = v₂ – v₁

- Áp dụng công thức tính gia tốc: a = \(\frac{{\Delta v}}{{\Delta t}}\).

Lời giải chi tiết:

a) Sự thay đổi tốc độ của quả bóng là:

υ₁ = 25 m/s; υ₂ = 15 m/s => \(\Delta \upsilon  = {\upsilon _1} - {\upsilon _2}\)= 25 – 15 = 10 m/s.

b) Chọn chiều dương theo hướng từ tây sang đông.

Ta có:

|\(\overrightarrow {{v_1}} \)| = 25 m/s (theo hướng đông) => v₁ = 25 m/s.

|\(\overrightarrow {{v_2}} \)| = 15 m/s (theo hướng tây) => v₂ = -15 m/s.

Sự thay đổi vận tốc của quả bóng là:

∆v = v₂ – v₁ = -15 – 25 = -40 m/s.

c) Gia tốc của quả bóng trong thời gian tiếp xúc với tường là:

a = \(\frac{{\Delta v}}{{\Delta t}}\)= \(\frac{{ - 40}}{{0,05}}\)= -800 m/s².

8.7

Hình 8.1 là đồ thị vận tốc - thời gian của một thang máy khi đi từ tầng 1 lên tầng 3 của toà nhà chung cư.

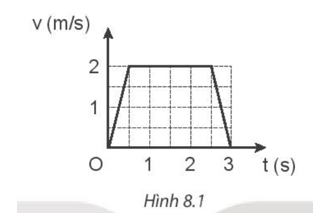
a) Mô tả chuyển động của thang máy.

b) Tính gia tốc của thang máy trong các giai đoạn.

Phương pháp giải:

- Dựa vào đặc điểm đồ thị để mô tả các loại chuyển động tưng ứng.

- Áp dụng công thức tính gia tốc: a = \(\frac{{\Delta v}}{{\Delta t}}\).

Lời giải chi tiết:

a) Từ 0 s đến 0,5 s: thang máy chuyển động nhanh dần đều từ dưới lên.

Từ 0,5 s đến 2,5 s: thang máy chuyển động đều.

Từ 2,5 s đến 3 s: thang máy chuyển động chậm dần đều và dừng lại.

b) Gia tốc của thang máy trong các giai đoạn lần lượt là:

a₁ = \(\frac{{\Delta {v_1}}}{{\Delta {t_1}}}\)= \(\frac{{2 - 0}}{{0,5 - 0}}\)=\(\frac{2}{{0,5}}\)= 4 m/s².

a₂ = \(\frac{{\Delta {v_2}}}{{\Delta {t_2}}}\)= \(\frac{{2 - 2}}{{2,5 - 0,5}}\)=\(\frac{0}{2}\)= 0 m/s².

a₃ = \(\frac{{\Delta {v_3}}}{{\Delta {t_3}}}\)= \(\frac{{0 - 2}}{{3 - 2,5}}\)=\(\frac{{ - 2}}{{0,5}}\)= -4 m/s².

8.8

Dựa vào bảng ghi sự thay đổi vận tốc theo thời gian của một ô tô chạy trên

quãng đường thẳng dưới đây.

 a) Vẽ đồ thị vận tốc – thời gian của chuyển động.

b) Tính gia tốc của ô tô trong 5 s đầu và kiểm tra kết quả tính được bằng đồ thị.

c) Tính gia tốc của ô tô trong 5 s cuối.

Phương pháp giải:

- Sử dụng bảng trên để vẽ đồ thị vận tốc – thời gian của chuyển động.

- Áp dụng công thức tính gia tốc: a = \(\frac{{\Delta v}}{{\Delta t}}\).

Lời giải chi tiết:

a) Từ các số liệu đã cho ta có đồ thị vận tốc – thời gian của chuyển động như sau:

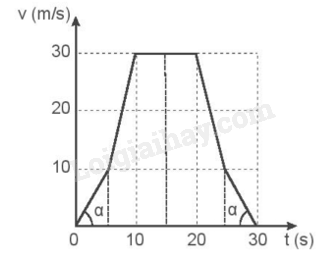
b) Gia tốc của ô tô trong 5 s đầu là: a₁ = \(\frac{{\Delta {v_1}}}{{\Delta {t_1}}}\)= \(\frac{{10 - 0}}{{5 - 0}}\)=\(\frac{{10}}{5}\)= 2 m/s².

- Kiểm tra lại bằng đồ thị:

Đồ thị vận tốc theo thời gian của chuyển động biến đổi đều là đường thẳng xiên góc xuất phát từ điểm (t₀, v₀), tạo với trục thời gian một góc α.

=> tan α = \(\frac{{v - {v_0}}}{{t - {t_0}}}\)= \(\frac{{10}}{5}\)= 2.

c) Gia tốc của ô tô trong 5 s cuối là: a₂ = \(\frac{{\Delta {v_2}}}{{\Delta {t_2}}}\)= \(\frac{{0 - 10}}{{30 - 25}}\)=\(\frac{{ - 10}}{5}\)= -2 m/s².

8.9

Một người lái xe máy đang chạy xe với vận tốc 36 km/h thì nhìn thấy một cái hố sâu trước mặt. Người ấy kịp thời phanh gấp xe thì xe tiếp tục chạy thêm 3s nữa mới dừng lại. Tính gia tốc trung bình của xe.

Phương pháp giải:

Áp dụng công thức tính gia tốc: a = \(\frac{{\Delta v}}{{\Delta t}}\).

Lời giải chi tiết:

Đổi 36 km/h = 10 m/s.

Gia tốc trung bình của xe là: a = \(\frac{{\Delta v}}{{\Delta t}}\)= \(\frac{{{v_s} - {v_t}}}{{\Delta t}}\)= \(\frac{{0 - 10}}{3}\)=\(\frac{{ - 10}}{3}\)≈ 3,33 m/s².

8.10

Một ô tô tải đang chạy trên đường thẳng với vận tốc 18 km/h thì tăng dần đều vận tốc. Sau 20 s, ô tô đạt được vận tốc 36 km/h.

a) Tính gia tốc của ô tô.

b) Tính vận tốc ô tô đạt được sau 40 s.

c) Sau bao lâu kể từ khi tăng tốc, ô tô đạt vận tốc 72 km/h.

Phương pháp giải:

- Áp dụng công thức tính gia tốc: a = \(\frac{{\Delta v}}{{\Delta t}}\).

- Viết phương trình vận tốc của chuyển động thẳng nhanh dần đều theo công thức: v₁ = v₀ + at₁. Thay số để tính vận tốc của ô tô.

- Viết phương trình vận tốc của chuyển động thẳng nhanh dần đều theo công thức: v₂ = v₀ + at₂. Giải phương trình để tính thời gian t.

Lời giải chi tiết:

Đổi v₀ = 18 km/h = 5 m/s. v₁ = 36 km/h = 10 m/s.

a) Gia tốc của ô tô là: a = \(\frac{{\Delta v}}{{\Delta t}}\)= \(\frac{{{v_1} - {v_0}}}{{\Delta t}}\)=\(\frac{{10 - 5}}{{20}}\)= 0,25 m/s².

b) Phương trình vận tốc của ô tô: v₁ = v₀ + at₁.

Với v₀ = 5 m/s; t₁ = 40 s; a = 0,25 m/s².

=> v₁ = 5 + 0,25 x 40 = 15 m/s.

c) Phương trình vận tốc của ô tô: v₂ = v₀ + at₂.

Với v₀ = 5 m/s; v₂ = 72 km/h = 20 m/s; a = 0,25 m/s².

Ta có: 20 = 5 + 0,25t => t = \(\frac{{20 - 5}}{{0,25}}\)= 60 s.