Trắc nghiệm 18.1
Đơn vị nào sau đây là đơn vị của động lượng?
A. N.s. B. N.m.
C. N.m/s. D. N/s.
Phương pháp giải:
Vận dụng kiến thức về khái niệm về động lượng.
Lời giải chi tiết:
Theo biểu thức của động lượng: p = m.v = F/a. v, với đơn vị của F là N, của a là m/s2, của v là m/s => một số đơn vị của động lượng: kg.m/s; N.s.
=> Chọn A
Trắc nghiệm 18.2
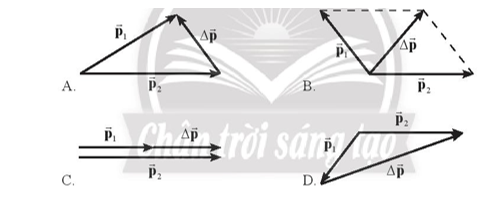
Trong các hình dưới đây, các hình vẽ nào biểu diễn đúng vecto độ biến thiên động lượng \(\Delta \overrightarrow p = \overrightarrow {{p_2}} - \overrightarrow {{p_1}} \)? (Có thể có nhiều hơn một đáp án đúng)
Phương pháp giải:
Vận dụng kiến thức về độ biến thiên động lượng.
Lời giải chi tiết:
Độ biến thiên động lượng: \(\Delta \overrightarrow p = \overrightarrow {{p_2}} - \overrightarrow {{p_1}} \) (phép trừ vecto).
=> Chọn C, D
Trắc nghiệm 18.3
Chọn từ/cụm từ thích hợp trong bảng dưới đây để điền vào chỗ trống.
|
vô hướng |
cùng chiều |
có thể |
N.m/s |
không thể |
vuông góc |
|
thương số |
có hướng |
tích số |
ngược chiều |
kg.m/s |
khối lượng |
Động lượng là một đại lượng (1) …, kí hiệu là \(\overrightarrow p \), luôn (2) … với vecto vận tốc \(\overrightarrow v \) của vật. Độ lớn của động lượng được xác định bằng (3) … giữa (4) … và tốc độ của vật. Đơn vị của động lượng là (5) … Động lượng (6) … truyền từ vật này sang vật khác.
Phương pháp giải:
Vận dụng kiến thức về động lượng.
Lời giải chi tiết:
(1) có hướng; (2) cùng chiều; (3) tích số; (4) khối lượng; (5) kg.m/s; (6) có thể
Trắc nghiệm 18.4
Biểu thức nào sau đây mô tả đúng mối quan hệ giữa động lượng và động năng của vật?
A. \(p = \sqrt {m.{W_d}} \) B. p = m. Wđ
C. \(p = \sqrt {2m.{W_d}} \) D. p = 2m. Wđ
Phương pháp giải:
Vận dụng kiến thức về động lượng và động năng.
Lời giải chi tiết:
Ta có: \(p = m.v;\,{W_d} = \frac{1}{2}m{v^2} \Rightarrow v = \sqrt {\frac{{2{W_d}}}{m}} \Rightarrow p = \sqrt {2m.{W_d}} \).
=> Chọn C
Trắc nghiệm 18.5
Trong các quá trình chuyển động sau đây, quá trình nào mà động lượng của vật không thay đổi?
A. Vật chuyển động chạm vào vách và phản xạ lại.
B. Vật đang ném ngang.
C. Vật đang rơi tự do.
D. Vật đang chuyển động thẳng đều.
Phương pháp giải:
Vận dụng kiến thức về động lượng.
Lời giải chi tiết:
Ta có động lượng được xác định bằng biểu thức: p = m.v, nên với các vật chuyển động thẳng đều (v = const) thì động lượng của vật không đổi.
=> Chọn D
Trắc nghiệm 18.6
Trong trường hợp nào sau đây, hệ có thể xem là hệ kín?
A. Hai viên bi chuyển động trên mặt phẳng nằm ngang.
B. Hai viên bi chuyển động trên mặt phẳng nghiêng.
C. Hai viên bi rơi thẳng đứng trong không khí.
D. Hai viên bi chuyển động không ma sát trên mặt phẳng nằm ngang.
Phương pháp giải:
Vận dụng kiến thức về hệ kín.
Lời giải chi tiết:
Một hệ được gọi là hệ kín khi hệ đó không tương tác với các vật bên ngoài hệ.
Các trường hợp A, B, C vật khi chuyển động chịu tác dụng của lực cản, lực ma sát (có sự tương tác với bên ngoài hệ) nên không phải là hệ kín.
=> Chọn D
Trắc nghiệm 18.7
Khi một vật đang rơi (không chịu tác dụng của lực cản không khí) thì
A. động lượng của vật không đổi.
B. động lượng của vật chỉ thay đổi về độ lớn.
C. động lượng của vật chỉ thay đổi về hướng.
D. động lượng của vật thay đổi cả về hướng và độ lớn.
Phương pháp giải:
Vận dụng kiến thức về định luật bảo toàn động lượng.
Lời giải chi tiết:
Động lượng của một hệ kín luôn được bảo toàn.
Khi vật đang rơi và không chịu tác dụng của lực cản không khí hay nói cách khác vật đang rơi tự do thì hệ vật chuyển động được xem là hệ kín.
=> Chọn B
Trắc nghiệm 18.8
Hai vật có khối lượng m1 và m2 chuyển động với vận tốc lần lượt là \(\overrightarrow {{v_1}} \) và \(\overrightarrow {{v_2}} \). Động lượng của hệ có giá trị
A. \(m.\overrightarrow v \)
B. \({m_1}.\overrightarrow {{v_1}} + {m_2}.\overrightarrow {{v_2}} \)
C. 0
D. m1.v1 + m2.v2
Phương pháp giải:
Vận dụng kiến thức về động lượng
Lời giải chi tiết:
Ta có: \(\overrightarrow {{p_1}} = {m_1}.\overrightarrow {{v_1}} ;\,\overrightarrow {{p_2}} = {m_2}.\overrightarrow {{v_2}} \Rightarrow \overrightarrow p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} = {m_1}.\overrightarrow {{v_1}} + {m_2}.\overrightarrow {{v_2}} \)
=> Chọn B
Tự luận 18.1
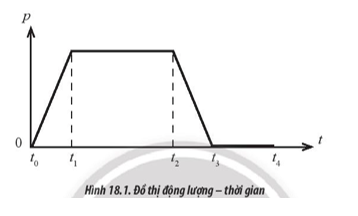
Từ đồ thị mô tả sự thay đổi của động lượng theo thời gian như Hình 18.1, hãy phân tích tính chất chuyển động của vật trong những khoảng thời gian từ t0 đến t1, từ t1 đến t2, từ t2 đến t3 và từ t3 đến t4.
Phương pháp giải:
Vận dụng kiến thức về động lượng: độ lớn của động lượng tỉ lệ thuận với vận tốc chuyển động của vật.
Lời giải chi tiết:
Từ t0 đến t1, vật chuyển động nhanh dần đều. Từ t1 đến t2, vật chuyển động đều. Từ t2 đến t3, vật chuyển động chậm dần đều. Từ t3 đến t4, vật đứng yên.
Tự luận 18.2
Một vật đang đứng yên trên mặt bàn nằm ngang không ma sát thì vỡ thành hai mảnh, trong đó mảnh A chuyển động theo chiều dương của trục Ox.
a) Vecto tổng động lượng của hệ hai mảnh vỡ là bao nhiêu?
b) Hãy xác định chiều vecto động lượng của mảnh B.
Phương pháp giải:
Vận dụng kiến thức về khái niệm về vecto động lượng: \(\overrightarrow p = m.\overrightarrow v \), trong đó: \(\overrightarrow p \) là động lượng của vật, m là khối lượng của vật, \(\overrightarrow v \) là vận tốc của vật.
Lời giải chi tiết:
a) Vì ban đầu vật đứng yên, tức động lượng của vật bằng 0. Do hệ là hệ kín nên theo định luật bảo toàn động lượng, vecto động lượng của hệ hai mảnh vỡ \(\overrightarrow p = \overrightarrow 0 \).
b) Để tổng động lượng hệ hai mảnh vỡ bằng 0 thì động lượng của mảnh B phải hướng ngược chiều dương của trục Ox (ngược chiều động lượng của mảnh A).
Tự luận 18.3
Trong giờ học môn Giáo dục quốc phòng và an ninh về nội dung sử dụng súng bắn AK, học sinh được giáo viên hướng dẫn rằng, trong quá trình ngắm bắn, ta cần phải tì báng súng vào hõm vai phải. Dựa trên kiến thức đã học về động lượng, hãy giải thích tại sao ta cần phải để báng súng như vậy.
Phương pháp giải:
Vận dụng kiến thức về định luật bảo toàn động lượng.
Lời giải chi tiết:
Theo định luật bảo toàn động lượng, khi đạn được bắn ra với vận tốc \(\overrightarrow v \) thì lúc này thân súng cũng sẽ chuyển động ngược chiều với vận tốc \(\overrightarrow V = - \frac{m}{M}.\overrightarrow v \). Do đó, nếu ta không tì báng súng vào hõm vai thì thân súng có thể sẽ giật lùi và va chạm vào mặt hay một số vị trí khác trên cơ thể làm ta bị thương trong quá trình sử dụng súng. Ngoài ra, việc tì báng súng vào hõm vai còn giúp tăng sự ổn định của súng để viên đạn bắn mục tiêu được chính xác hơn.
Tự luận 18.4
Một ô tô có khối lượng 1 tấn đang chuyển động với tốc độ 60 km/h và một xe tải có khối lượng 2 tấn đang chuyển động với tốc độ 10 m/s. Tính tỉ số độ lớn động lượng của hai xe.
Phương pháp giải:
Vận dụng kiến thức về động lượng.
Lời giải chi tiết:
Tóm tắt:
moto = 1 tấn = 1000 kg
voto = 60 km/h
mxe tải = 2 tấn = 2000 kg
vxe tải = 10 m/s
poto/pxe tải =?
Lời giải:
\(\frac{{{p_{oto}}}}{{{P_{xe\,tai}}}} = \frac{{{m_{oto}}.{v_{oto}}}}{{{m_{xe\,tai}}.{v_{xe\,tai}}}} = \frac{{1000.\left( {60/3,6} \right)}}{{2000.10}} = \frac{5}{6}.\)
Tự luận 18.5
Một hệ gồm hai vật có khối lượng và tốc độ lần lượt là m1 = 200 g, m2 = 100 g và v1 = 2 m/s, v2 = 3 m/s. Xác định vecto động lượng của hệ trong các trường hợp sau:
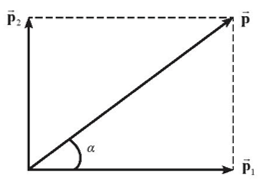
a) Hai vật chuyển động theo hai hướng vuông góc với nhau.
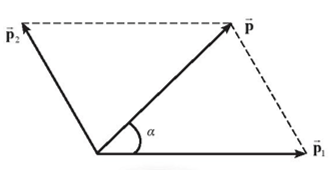
b) Hai vật chuyển động theo hai hướng hợp với nhau một góc 1200.
Phương pháp giải:
Vận dụng kiến thức về khái niệm động lượng.
Lời giải chi tiết:
Ta có:
m1 = 200 g
m2 = 100 g
v1 = 2 m/s
v2 = 3 m/s
Động lượng của hai vật lần lượt có độ lớn: p1 = m1.v1 = 0,4 kg.m/s, p2 = m2.v2 = 0,3 kg.m/s.
Động lượng của hệ: \(\overrightarrow p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} \)
a) \(p = \sqrt {p_1^2 + p_2^2} = 0,5kg.m/s\)
\(\tan \alpha = \frac{{{P_2}}}{{{P_1}}} \Rightarrow \alpha \approx {37^0}\)
b) \(p = \sqrt {p_1^2 + p_2^2 + 2{p_1}{p_2}\cos \theta } \approx 0,36kg.m/s\)
\(\cos \alpha = \frac{{{p^2} + p_1^2 - p_2^2}}{{2p.{p_1}}} = 0,7 \Rightarrow \alpha = {46^0}\)
Tự luận 18.6
Một quả bóng có khối lượng 50 g đang bay theo phương ngang với tốc độ 2 m/s thì va chạm vào tường và bị bật trở lại với cùng một tốc độ. Tính độ biến thiên động lượng và quả bóng.
Phương pháp giải:
Vận dụng kiến thức về định lí biến thiên động lượng.
Lời giải chi tiết:
Tóm tắt:
m = 50 g
v = 2 m/s
\(\Delta \overrightarrow p = ?\)
Lời giải:
Chọn chiều dương là chiều chuyển động của quả bóng sau va chạm.
Độ biến thiên động lượng: \(\Delta \overrightarrow p = \overrightarrow {{p_2}} - \overrightarrow {{p_1}} = m.\left( {\overrightarrow {{v_2}} - \overrightarrow {{v_1}} } \right).\)
Chiếu lên chiều dương: \(\Delta p = m\left( {{v_2} + {v_1}} \right) = 0,05.\left( {2 + 2} \right) = 0,2kg.m/s\).
Tự luận 18.7
Xạ thủ Nguyễn Minh Châu là người giành huy chương vàng ở nội dung 10 m súng ngắn hơi nữ ngay lần đầu tham dự SEA Games 27. Khẩu súng chị sử dụng nặng 1,45 kg với viên đạn nặng 7,4 g. Tốc độ đạn khi rời khỏi nòng là 660 fps (1 fps = 0,3 m/s). Hỏi khi bắn, nòng súng giật lùi với tốc độ bao nhiêu?
Phương pháp giải:
Vận dụng kiến thức về định luật bảo toàn động lượng.
Lời giải chi tiết:
Tóm tắt:
ms = 1,45 kg
mđ = 7,4 g
vđ = 660 fps = 198 m/s.
vs’ =?
Lời giải:
Áp dụng định luật bảo toàn động lượng:
\(\overrightarrow {{p_s}} + \overrightarrow {{p_d}} = \overrightarrow {{p_s}} ' + \overrightarrow {{p_d}} ' \Rightarrow 0 = {m_s}.\overrightarrow {{v_s}} ' + {m_d}.\overrightarrow {{v_d}} ' \Rightarrow \overrightarrow {{v_s}} ' = - \frac{{{m_d}.\overrightarrow {{v_d}} '}}{{{m_s}}}\)
Tốc độ giật lùi của súng: \({v_s}' = \frac{{{m_d}.{v_d}'}}{{{m_s}}} = 1m/s.\)
Tự luận 18.8
Hạt nhân uranium đang đứng yên thì phân rã (vỡ) thành hai hạt: hạt \(\alpha \) có khối lượng 6,65.10-27 kg và hạt X có khối lượng 3,89.10-25 kg.
a) Giải thích tại sao hạt nhân sau khi phân rã chuyển động theo hai hướng ngược nhau.
b) Tính tỉ số v0/vx.
Phương pháp giải:
Vận dụng kiến thức về định luật bảo toàn động lượng.
Lời giải chi tiết:
Tóm tắt:
\({m_\alpha } = 6,{65.10^{ - 27}}kg\)
mX = 3,89.10-25 kg
v0/vX =?
Lời giải:
a) Động lượng ban đầu: \(\overrightarrow {{p_t}} = \overrightarrow {{p_U}} = 0.\)
Động lượng của hệ sau khi phân rã: \(\overrightarrow {{p_s}} = \overrightarrow {{p_\alpha }} + \overrightarrow {{p_X}} \)
Áp dụng định luật bảo toàn động lượng suy ra: \(\overrightarrow {{p_\alpha }} = - \overrightarrow {{p_X}} \left( * \right)\).
Vậy sau khi uranium phân rã, hạt \(\alpha \) và hạt X chuyển động theo hai hướng ngược nhau.
b) Từ (*) suy ra: \({p_\alpha } = {p_X} \Rightarrow {m_\alpha }.{v_\sigma } = {m_X}.{v_X} \Rightarrow \frac{{{v_\alpha }}}{{{v_X}}} = \frac{{{m_X}}}{{{m_\alpha }}} = 58,5.\)
