Câu hỏi tr 95
| Mở đầu: Sự va chạm giữa các ô tô khi tham gian giao thông, có thể ảnh hưởng lớn đến trạng thái của xe, thậm chí nguy hiểm đến tính mạng người ngồi trong xe. Để nâng cao độ an toàn của ô tô, giảm hậu quả của lực tác dụng lên người lái, cần phải hiểu điều gì sẽ xảy ra với ô tô bị va chạm khi đang chuyển động. Những đặc điểm nào của ô tô ảnh hưởng đến hậu quả va chạm? |
Phương pháp giải:
Liên hệ thực tế
Lời giải chi tiết:
Đặc điểm của ô tô ảnh hưởng đến hậu quả va chạm là: ô tô có động cơ vượt trội hơn hẳn các xe khác nên vận tốc tối đa của ô tô rất lớn, chính vì vậy người lái xe ô tô thường đi với tốc độ rất lớn và dễ dẫn đến va chạm.
Câu hỏi tr 96
Quan sát, trả lời câu hỏi và thảo luận
|
Hãy đề xuất phương án và thực hiện thí nghiệm để chứng tỏ tốc độ và khối lượng của vật khi va chạm càng lớn thì hậu quả do va chạm càng lớn |
Phương pháp giải:
Vận dụng kiến thức đã học và thực hiện thí nghiệm
Lời giải chi tiết:
Phương án thí nghiệm: Thả các viên bi có cùng kích thước nhưng khối lượng khác nhau xuống một khối đất nặn. Căn cứ vào độ lún của viên bi vào khối đất nặn, ta có thể đánh giá được tác động của viên bi đang chuyển động đối với vật cản là đất nặn
Thực hiện thí nghiệm:
+ Lần lượt thả một viên bi để nó chạm vào đất nặn với các tốc độ khác nhau.
+ Lần lượt thả các viên bi cùng kích thước nhưng có khối lượng khác nhau để chúng chạm vào đất nặn với cùng tốc độ
=> Kết quả:
+ Với cùng một viên bi, tốc độ khi va chạm càng lớn, nó càng lún sâu vào đất nặn
+ Với các viên bi cùng kích thước, viên bi nào khối lượng càng lớn, càng lún sâu vào đất nặn
=> Độ lún sâu vào đất nặn của viên bi phụ thuộc vào cả khối lượng và tốc độ của nó khi va chạm.
Quan sát, trả lời câu hỏi và thảo luận
|
Làm thế nào để một viên bi có tốc độ khác nhau khi tiếp xúc với đất nặn |
Phương pháp giải:
Vận tốc của vật rơi tự do phụ thuộc vào độ cao: \(v = \sqrt {2gh} \)
Lời giải chi tiết:
Thả viên bi ở độ cao khác nhau thì vận tốc của viên bi sẽ khác nhau khi tiếp xúc với đất nặn.
Luyện tập
|
Tính độ lớn động lượng của từng vật sau: a) Một hòn đá khối lượng 0,5 kg đang chuyển động với vận tốc 20 m/s. b) Một chiếc xe buýt khối lượng 12 000 kg đi với tốc độ 10 m/s trên đường c) Một eletron di chuyển với tốc độ 2,0.107 m/s (Khối lượng của electron là 9,1.10 -31 kg.) |
Phương pháp giải:
Biểu thức tính động lượng: p = m.v
Lời giải chi tiết:
a) Ta có: m = 0,5 kg; v = 20 m/s.
=> Động lượng của hòn đá là: p = m.v = 0,5.20 = 10 (kg.m/s).
b) Ta có: m = 12 000 kg; v = 10 m/s.
=> Động lượng của xe buýt là: p = m.v = 12 000.10 = 1,2.105 (kg.m/s).
c) Ta có: m = 9,1.10 -31 kg; v = 2,0.107 m/s.
=> Động lượng của electron là: p = m.v = 9,1.10 -31 . 2,0.107 = 1,82.10-23 (kg.m/s)
Câu hỏi tr 97
Quan sát, trả lời câu hỏi và thảo luận
|
Hãy biểu diễn độ thay đổi động lượng của từng xe sau khi va chạm (hình 1.2)
|
Lời giải chi tiết:
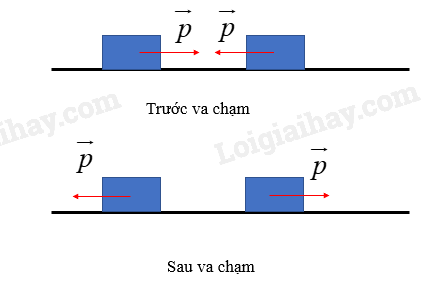
Quan sát, trả lời câu hỏi và thảo luận
|
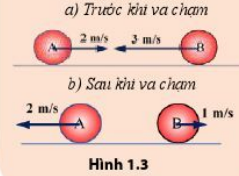
Hai quả cầu A và B, mỗi quả có khối lượng 1 kg, va chạm nhau như trong hình 1.3. Hãy tính tổng động lượng của hai quả cầu trước va chạm và tổng động lượng của chúng sau va chạm. So sánh kết quả và nêu kết luận
|
Phương pháp giải:
Biểu thức tính động lượng: p = m.v
Lời giải chi tiết:
Chọn chiều dương là chiều từ trái sang phải
+ Trước khi va chạm: v1 = 2 m/s; v2 = 3 m/s
=> Động lượng của vật trước va chạm: p = m.v1 – m.v2 = m.(v1 – v2 ) = 1.(-1) = -1 (kg.m/s)
+ Sau va chạm: \(v_1' = 2\) m/s; \(v_2' = 1\) m/s
=> Động lượng của vật sau va chạm: \(p = m.( - v_1' + v_2') = 1.( - 1) = - 1(kg.m/s)\)
=> Động lượng trước va chạm = Động lượng sau va chạm
=> Kết luận: Trong quá trình chuyển động của vật, động lượng được bảo toàn
Câu hỏi tr 98
Quan sát, trả lời câu hỏi và thảo luận
|
Dựa vào định luật bảo toàn động lượng, hãy thiết lập công thức tính tốc độ của hai xe trên giá đỡ nằm ngang, trong trường hợp một xe có tốc độ đã biết tới va chạm với xe còn lại đang đứng yên, sau va chạm hai xe dính vào nhau và cùng chuyển động. |
Phương pháp giải:
Định luật bảo toàn động lượng: \(\sum {\overrightarrow {{p_{tr}}} = \sum {\overrightarrow {{p_s}} } } \)
Lời giải chi tiết:
Gọi xe 1 có khối lượng, vận tốc trước va chạm, vận tốc sau va chạm là m1 , v1 , v’1
Xe 2 có khối lượng, vận tốc trước va chạm, vận tốc sau va chạm là m2 , v2 , v’2
Giả sử xe 1 có tốc độ va chạm với xe 2 đang đứng yên
=> v2 = 0
Sau va chạm hai xe dính vào nhau, nên ta có \(v_1' = v_2' = {v'}\)
Chọn chiều dương là chiều chuyển động của xe 1
Áp dụng định luật bảo toàn khối lượng ta có:
\(\overrightarrow {{p_1}} + \overrightarrow {{p_2}} = \overrightarrow {p_1'} + \overrightarrow {p_2'} \)
\( \Leftrightarrow {m_1}.\overrightarrow {{v_1}} + {m_2}.\overrightarrow {{v_2}} = ({m_1} + {m_2}).\overrightarrow {{v'}} \) (1)
Chiếu (1) lên chiều dương, ta có: \({m_1}.{v_1} + {m_2}.{v_2} = ({m_1} + {m_2}).{v'}\)
Do v2 = 0 \( \Rightarrow {v'} = \frac{{{m_1}.{v_1}}}{{{m_1} + {m_2}}}\)
Quan sát, trả lời câu hỏi và thảo luận
|
Kết quả thí nghiệm đo được trong một lần thí nghiệm với hai xe có cùng khối lượng là 245 g, xe 1 có tốc độ 0,542 m/s va chạm với xe 2 đang đứng yên, sau va chạm đo được hai xe có cùng tốc độ là 0,269 m/s. Hãy tính động lượng của từng xe trước và sau va chạm, từ đó so sánh động lượng của hệ hai xe trước và sau va chạm. Định luật bảo toàn có được nghiệm đúng hay không? |
Phương pháp giải:
Biểu thức tính động lượng: p = m.v
Lời giải chi tiết:
Động lượng của các xe trước va chạm:
+ Xe 1: \({p_1} = {m_1}.{v_1} = 0,245.0,542 \approx 0,133(kg.m/s)\)
+ Xe 2: \({p_2} = {m_2}.{v_2} = 0\)(do xe 2 đứng yên nên v2 = 0)
=> Động lượng của hệ trước va chạm là: p = 0,133 kg.m/s
Động lượng của các xe sau va chạm
+ Xe 1: \(p_1' = {m_1}.v_1' = 0,245.0,269 \approx 0,066(kg.m/s)\)
+ Xe 2: \(p_2' = {m_2}.v_2' = 0,245.0,269 \approx 0,066(kg.m/s)\)
=> Động lượng của hệ sau va chạm là: p’ = 0,132 kg.m/s
=> Động lượng của hệ trước và sau va chạm gần như bằng nhau
=> Định luật bảo toàn động lượng được nghiệm đúng.
Quan sát, trả lời câu hỏi và thảo luận
|
Ngay trước khi nổ, quả pháo hoa có tốc độ bằng không, động lượng của nó bằng không. Ngay sau khi nổ, các mảnh pháo hoa bay ra theo mọi hướng , mỗi mảnh có động lượng khác không. Điều này có mâu thuẫn với định luật bảo toàn động lượng hay không? |
Lời giải chi tiết:
Trong một hệ kín, nếu có một phần của hệ chuyển động theo một hướng, theo định luật bảo toàn động lượng, phần còn lại của hệ phải chuyển động theo hướng ngược lại.
Khi quả pháo hoa được bắn thẳng đứng lên cao và phát nổ đúng khi tới điểm cao nhất. Ta thấy các mảnh pháo hoa cháy rực rỡ nhiều màu và bay ra theo mọi hướng, mỗi mảnh nhỏ đều có động lượng, luôn có mảnh khác tương ứng chuyển động theo hướng ngược lại. Nên điều này không mẫu thuẫn với định luật bảo toàn động lượng.
Câu hỏi tr 99
Vận dụng: Một quả bóng bay theo phương ngang tới va chạm vào tường thẳng đứng với cùng vận tốc ở hai lần khác nhau. Lần thứ nhất, quả bóng bị nảy ngược lại cùng tốc độ ngay trước khi va chạm vào tường. Lần thứ hai, quả bóng bay tới và bị dính vào tường.
| Câu 1: Trong lần nào quả bóng có độ thay đổi động lượng lớn hơn? |
Phương pháp giải:
Biểu thức tính động lượng: p = m.v
Lời giải chi tiết:
Độ thay đổi động lượng: \(\Delta p = \left| {{p_s} - {p_{tr}}} \right|\)
Chọn chiều dương là chiều chuyển động của bóng khi va chạm vào tường.
+ Lần thứ nhất: \(\Delta p = \left| {{p_s} - {p_{tr}}} \right| = \left| { - mv - mv} \right| = 2mv\)
+ Lần thứ hai: \(\Delta p = \left| {{p_s} - {p_{tr}}} \right| = \left| {0 - mv} \right| = mv\)
=> Trong lần thứ nhất, quả bóng có độ thay đổi động lượng lớn hơn.
| Câu 2: Giả sử khoảng thời gian biến đổi động lượng của quả bóng khi va vào tường trong hai lần là bằng nhau, lần nào lực trung bình quả bóng tác dụng lên tường lớn hơn? |
Phương pháp giải:
Độ biến thiên động lượng của một vật trong một khoảng thời gian nào đó bằng xung lượng của lực tác dụng lên vật trong khoảng thời gian đó: \(\Delta \overrightarrow p = \overrightarrow F .\Delta t\)
Lời giải chi tiết:
+ Nếu khoảng thời gian biến đổi động lượng của quả bóng trong hai lần là bằng nhau, thì ta có lực trung bình tỉ lệ thuận với độ biến thiên động lượng.
+ Độ biến thiên động lượng trong lần thứ nhất lớn hơn độ biến thiên động lượng trong lần thứ hai nên lực trung bình của quả bóng trong lần thứ nhất lớn hơn lực trung bình của quả bóng tác dụng lên tường lần thứ hai.
| Câu 3: Động lượng của quả bóng có bảo toàn trong quá trình bóng va vào tường hay không? Giải thích. |
Phương pháp giải:
Định luật bảo toàn động lượng: \(\sum {\overrightarrow {{p_{tr}}} = \sum {\overrightarrow {{p_s}} } } \)
Lời giải chi tiết:
+ Lần thứ nhất: động lượng của quả bóng được bảo toàn.
+ Lần thứ hai: động lượng của quả bóng không được bảo toàn.
Vận dụng
|
Hãy sử dụng các vật liệu dễ kiếm để chế tạo xe đồ chơi có thể chuyển động bằng phản lực? |
Phương pháp giải:
Vận dụng kiến thức đã học
Lời giải chi tiết:
- Nguyên liệu:
+ 1 ống hút
+ 1 chai nhựa
+ 4 nắp chai
+ Băng dính
+ 1 quả bóng bay
- Chế tạo: