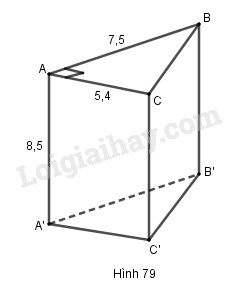
Hình lăng trụ đứng tam giác \(ABC.A'B'C'\) có độ dài đường cao \(AA' = 8,5cm\). Đáy \(ABC\) là tam giác vuông tại đỉnh \(A\), có độ dài các cạnh \(AB = 7,5cm;AC = 5,4cm\) (h.79).
Khoanh tròn vào chữ cái đứng trước khẳng định đúng.
LG a
Chu vi đáy (lấy đến hai chữ số thập phân) là:
A. \(22,14\) B. \(22,15\)
C. \(22,41\) D. \(22,51\)
Phương pháp giải:
Chu vi tam giác bằng tổng các cạnh.
Lời giải chi tiết:
Tam giác \(ABC\) vuông tại \(A\) nên theo định lí Pi – ta – go ta có:
\(B{C^2} = A{B^2} + A{C^2}\) \( = 7,{5^2} + 5,{4^2} = 85,41\) \( \Rightarrow BC \approx 9,24\)
Chu vi đáy: \(AB + AC + BC\) \( \approx 7,5 + 5,4 + 9,24 = 22,14\)
Chọn A.
LG b
Diện tích xung quanh của lăng trụ đứng (lấy đến hai chữ số thập phân) là:
A. \(188,20\) B. \(188,26\)
C. \(66,74\) D. \(53,60\)
Phương pháp giải:
Diện tích xung quanh \({S_{xq}} = {C_{đáy}}.h\) (diện tích xung quanh bằng chu vi đáy nhân chiều cao lăng trụ)
Lời giải chi tiết:
Diện tích xung quanh là:
\({S_{xq}} = {C_{đáy}}.AA' = 22,14.8,5 \approx 188,20\)
Chọn A.
LG c
Diện tích toàn phần của lăng trụ đứng (lấy đến hai chữ số thập phân) là:
A. \(228,71\) B. \(228,75\)
C. \(228,70\) D. \(229\)
Phương pháp giải:
Diện tích toàn phần \({S_{tp}} = {S_{xq}} + 2{S_đ}\).
Lời giải chi tiết:
Diện tích đáy là:
\({S_{ABC}} = \dfrac{1}{2}AB.AC\) \( = \dfrac{1}{2}.7,5.5,4 = 20,25\)
Diện tích toàn phần \({S_{tp}} = {S_{xq}} + 2{S_{ABC}}\) \( = 188,20 + 2.20,25 = 228,70\)
Chọn C.
dapandethi.vn
