Câu 26.
Tập hợp giao điểm hai đường thẳng chéo nhau của hình chữ nhật \(ABCD\) có \(A\) và \(B\) cố định là
(A) đường trung trực của \(AD\)
(B) đường trung trực của \(AB\)
(C) đường trung trực của \(BC\)
(D) đường tròn \((A;AB)\).
Phương pháp giải:
Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
Lời giải chi tiết:
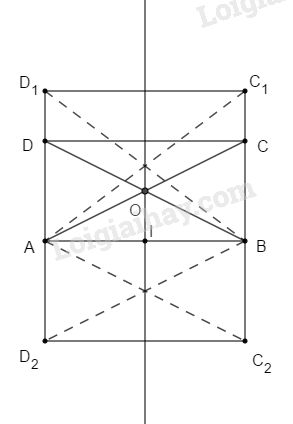
Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\).
Theo tính chất hình chữ nhật ta có: \(OA=OB\) nên \(O\) thuộc đường trung trực của đoạn thẳng \(AB.\)
Chọn B.
Câu 27.
Cho tam giác \(ABC\) cố định, điểm \(M\) đi chuyển trên cạnh \(BC\). Tập hợp các trung điểm của đoạn thẳng \(AM\) là
(A) đường tròn tâm \(A\) bán kính \(\dfrac{{AM}}{2}\)
(B) tia phân giác của góc \(A\)
(C) đường trung trực của \(BC\).
(D) đoạn thẳng \(DE\) trong đó \(D\) là trung điểm của \(AB, E\) là trung điểm của \(AC\).
Phương pháp giải:
Các điểm cách đường thẳng \(b\) một khoảng bằng \(h\) nằm trên hai đường thẳng song song với \(b\) và cách \(b\) một khoảng bằng \(h.
Lời giải chi tiết:
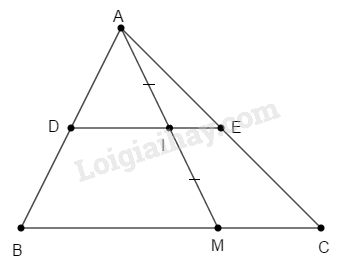
Gọi \(I\) là trung điểm của \(AM\); \(D; E\) lần lượt là trung điểm của \(AB;AC\).
Khi \(M \equiv B\) thì \(I \equiv D\); \(M \equiv C\) thì \(I \equiv E\).
Vậy khi \(M\) di chuyển trên \(BC\) thì \(I\) di chuyển trên đoạn thẳng \(DE\).
Chọn D.
dapandethi.vn
