1. Phân thức đối
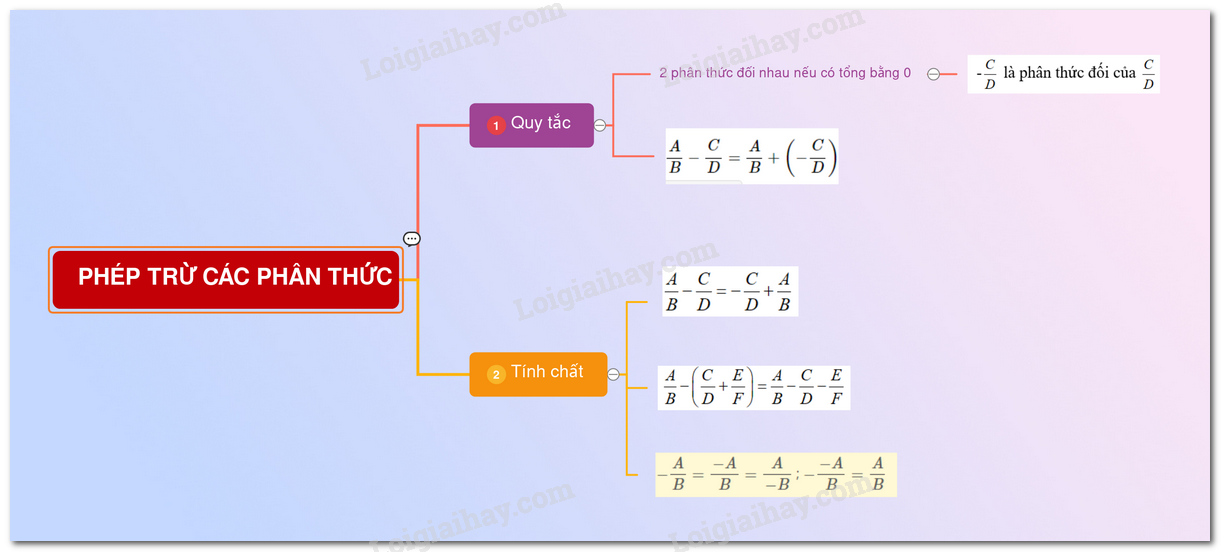
Hai phân thức được gọi là đối nhau nếu tổng của chúng bằng \(0\).
Phân thức đối của phân thức \( \dfrac{A}{B}\) được kí hiệu là \( -\dfrac{A}{B}\)
Vậy \( -\dfrac{A}{B} =\dfrac{-A}{B}\) và \( -\dfrac{-A}{B}=\dfrac{A}{B}\)
Ví dụ: \(\dfrac{x}{x-2}\) là phân thức đối của phân thức \(\dfrac{-x}{x-2}\)
2. Phép trừ
Quy tắc: Muốn trừ phân thức \( \dfrac{A}{B}\) cho phân thức \( \dfrac{C}{D}\), ta cộng \( \dfrac{A}{B}\) với phân thức đối của \( \dfrac{C}{D}\)
Vậy: \( \dfrac{A}{B}-\dfrac{C}{D}=\dfrac{A}{B}+\left( { - \dfrac{C}{D}} \right)\).
Ví dụ:
\( \dfrac{4x-1}{3x^{2}y}-\dfrac{7x-1}{3x^{2}y}\) \( =\dfrac{4x-1}{3x^{2}y}+\dfrac{-(7x-1)}{3x^{2}y}\)
\( =\dfrac{4x-1-7x+1}{3x^{2}y}\) \( =\dfrac{-3x}{3x^{2}y}=-\dfrac{1}{xy}\).