Đề bài
Quan sát tứ giác ABCD trong hình 18, hã điền vào chỗ trống (…) để chứng minh AB//CD và AD//BC. Từ đó, suy ra tứ giác ABCD là hình bình hành.
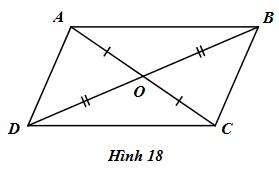
Xét hai tam giác AOB và COD, ta có:
OA = ……
….. = OD
\(\widehat {AOB} = ......\) (đối đỉnh).
Do đó \(\Delta ...... = \Delta .....\)
Suy ra \(\widehat {ABO} = .......\) mà hai góc này ở vị trí so le nhau , nên : …. // …. (1)
Chứng mình tương tự, ta cũng được :\( ….. // ….. (2)\)
Từ (1) và (2) suy ra tứ giác ABCD là hình ……
Lời giải chi tiết
Xét hai tam giác AOB và COD có:
\(\eqalign{ & OA = OC \cr & OB = OD \cr & \widehat {AOB} = \widehat {COD}\,\,\left( {đối\,\,đỉnh} \right) \cr & \Rightarrow \Delta AOB = \Delta COD\,\,\left( {c.g.c} \right) \Rightarrow \widehat {ABO} = \widehat {CDO} \cr} \)
Mà hai góc này ở vị trí so le trong, nên \(AB // CD (1)\)
Chứng minh tương tự, ta cũng được \(AD // BC (2)\)
Từ (1) và (2) suy ra tứ giác ABCD là hình bình hành.
dapandethi.vn
