Đề bài
Cho tam giác ABC, vẽ đường cao AH. Đặt BC = a, AH = h. Điền vào chỗ trống (…) trong bảng sau:
|
Trường hợp |
Vị trí điểm H trên BC |
Hình vẽ |
|
Tính SABC theo a và h |
|
1 |
\(H \equiv B\) |
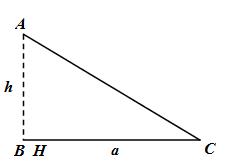 |
\({S_{ABC}} = {S_{AHC}} = \) |
.......... |
|
2 |
H thuộc đoạn BC |
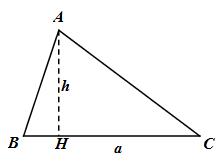 |
\(\eqalign{ & \,\,\,\,\,\,\,\,\,\,{S_{ABC}} \cr & = {S_{ABH}} + {S_{ACH}} \cr & = {1 \over 2}AH\left( {BH + CH} \right) \cr & = \cr} \) |
.......... |
|
3 |
H nằm ngoài đoạn BC |
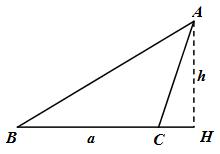 |
\(\eqalign{ & \,\,\,\,\,\,\,\,\,\,\,{S_{ABC}} \cr & = {S_{ABH}} - {S_{ACH}} \cr & = {1 \over 2}AH\left( {BH - CH} \right) \cr & = \cr} \) |
.......... |
Lời giải chi tiết
|
Trường hợp |
Vị trí điểm H trên BC |
Hình vẽ |
|
Tính SABC theo a và h |
|
1 |
\(H \equiv B\) |

|
\({S_{ABC}} = {S_{AHC}} = \) |
\({1 \over 2}ah\) |
|
2 |
H thuộc đoạn BC |

|
\(\eqalign{ & \,\,\,\,\,\,\,\,\,\,{S_{ABC}} \cr & = {S_{ABH}} + {S_{ACH}} \cr & = {1 \over 2}AH\left( {BH + CH} \right) \cr & = \cr} \) |
\({1 \over 2}ha\) |
|
3 |
H nằm ngoài đoạn BC |

|
\(\eqalign{ & \,\,\,\,\,\,\,\,\,\,\,{S_{ABC}} \cr & = {S_{ABH}} - {S_{ACH}} \cr & = {1 \over 2}AH\left( {BH - CH} \right) \cr & = \cr} \) |
\({1 \over 2}ha\) |
dapandethi.vn
