Đề bài
Bài 1. Tính đường cao của tam giác vuông biết hai cạnh góc vuông là 6 cm và 8 cm.
Bài 2. Cho tứ giác ABCD. Gọi M là trung điểm của AB, N là trung điểm của CD.
Chứng minh rằng: \({S_{MBN{\rm{D}}}} = {1 \over 2}{S_{ABCD}}.\)
Bài 3. Cho hình bình hành ABCD có I, J lần lượt là trung điểm của AB và CD.
a) Chứng minh AICJ là hình bình hành.
b) Biết diện tích hình bình hành ABCD bằng \(48c{m^2}\) . Tính diện tích AICJ.
c) Gọi E, F lần lượt là giao điểm của AJ, CJ với BD.
Chứng minh rằng BD = 3DE.
LG bài 1
Phương pháp giải:
Sử dụng định lý Py-ta-go
và \({S_{ABC}} = {1 \over 2}BC.AH = {1 \over 2}AB.AC\)
Lời giải chi tiết:
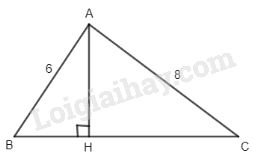
Ta có: \(B{C^2} = A{B^2} + A{C^2}\)
\( = {6^2} + {8^2}\) (định lý Py – ta – go)
\( \Rightarrow BC = \sqrt {36 + 64} = \sqrt {100} = 10\left( {cm} \right)\)
\({S_{ABC}} = {1 \over 2}BC.AH = {1 \over 2}AB.AC\)
\( \Rightarrow BC.AH = AB.AC\)
\(\Rightarrow AH = \dfrac{AB.AC}{10} = 6,8\left( {cm} \right)\)
LG bài 2
Phương pháp giải:
Nối B với D, chứng minh các tam giác có đáy bằng nhau và chung chiều cao nên diện tích bằng nhau
Lời giải chi tiết:
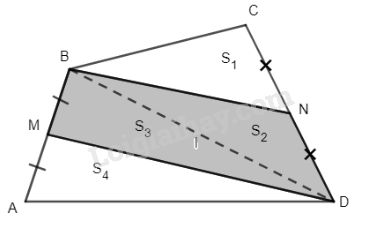
Nối đường chéo BD, \(\Delta BCD\) có BN là trung tuyến nên \({S_1} = {S_2}\) (đáy bằng nhau, chung đường cao)
Tương tự: \({S_3} = {S_4}\)
\( \Rightarrow {S_2} + {S_3} = {S_1} + {S_4} = {1 \over 2}{S_{ABCD}}.\)
Hay \({S_{MBND}} = {1 \over 2}{S_{ABCD}}.\)
LG bài 3
Phương pháp giải:
Sử dụng:
a.Tứ giác có 1 cặp cạnh đối song song và bằng nhau là hình bình hành
b. Nối đường chéo AC và chỉ ra các tam giác có diện tích bằng nhau
c.Đường trung bình của tam giác
Lời giải chi tiết:
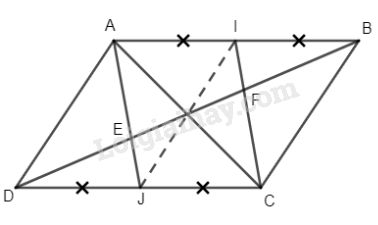
a) Ta có: \(AB// CJ\) và AI = CJ nên AICJ là hình bình hành.
b) Ta nối đường chéo AC ta có:
\({S_{ADJ}} = {S_{ACJ}} = {S_{ACI}} = {S_{BCI}}\) do đó
\({S_{ACJ}} + {S_{ACI}} = {S_{ADJ}} + {S_{BCI}} = {1 \over 2}{S_{ABCD}}\)
Hay \({S_{AICJ}} = {1 \over 2}{S_{ABCD}} = 24c{m^2}\).
c) Ta có \(IF//AE\) và I là trung điểm của AB (gt) nên IF là đường trung bình của \(\Delta ABE\) nên F là trung điểm của EB hay FE = FB.
Tương tự ta có E là trung điểm của DF nên FD = EF.
Vậy DE = EF = FB hay BD = 3DE.
Chú ý: Các bạn có thể giải câu c) bài 3 bằng cách khác: ta có E, F là trọng tâm các tam giác ACD và ABC.
dapandethi.vn
