Đề bài
Cho hình thoi ABCD. Trên các cạnh AB và BC lần lượt lấy hai điểm E và F sao cho BE + BF = BD. Chứng minh rằng \(\Delta DEF\) là tam giác đều.
Phương pháp giải - Xem chi tiết
Sử dụng:
Hình thoi có 4 cạnh bằng nhau và các góc đối bằng nhau
Tam giác cân có 1 góc bằng \(60^0\) là tam giác đều
Lời giải chi tiết
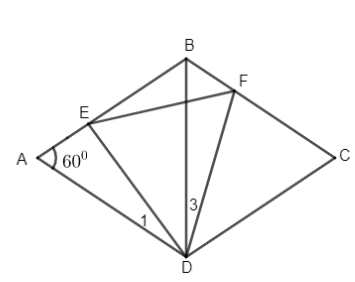
Ta có \(AB = AD(gt)\) và \(\widehat A = {60^ \circ }\) nên \(\Delta ABD\) đều \( \Rightarrow BD = AD.\)
Vì ABCD là hình thoi nên \(\widehat C=\widehat A = {60^ \circ }\) và \(CB=CD\)
Suy ra \(\Delta ABD\) đều \( \Rightarrow \widehat {CBD} = {60^ \circ }\)
Từ \(BE + BF = BD \Rightarrow AE = BF\)
Xét \(\Delta AED\) và \(\Delta BFD\) có:
\(AD = BD\left( {cmt} \right);\)
\(\widehat A = \widehat {CBD} = {60^ \circ };\)
\(AE = BF\)
Do đó \(\Delta AED = \Delta BFD\left( {c.g.c} \right)\)
\(\Rightarrow DE = DF\) nên \(\Delta DEF\) cân (1)
Và \(\widehat {{D_1}} = \widehat {{D_3}}\) mà \(\widehat {{D_1}} + \widehat {EDB} = {60^ \circ } \) \(\Rightarrow \widehat {{D_3}} + \widehat {EDB} = {60^ \circ }\) (2)
Từ (1) và (2) suy ra tam giác DEF đều.
dapandethi.vn
