Đề bài
Cho tam giác ABC. Từ đỉnh A kẻ các đường thẳng AP, AQ theo thứ tự vuông góc với các tia phân giác trong và phân giác ngoài của góc B, các đường thẳng AR, AS theo thứ tự vuông góc với các ta phân giác trong và ngoài của góc C.
a) Chứng minh tứ giác APBQ là hình chữ nhật.
b) Chứng minh rằng 4 điểm Q, R, P, S thẳng hàng.
Phương pháp giải - Xem chi tiết
Sử dụng:
Hai tia phân giác của hai góc kề bù thì vuông góc với nhau
Tứ giác có ba góc vuông là hình chữ nhật.
Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
Lời giải chi tiết
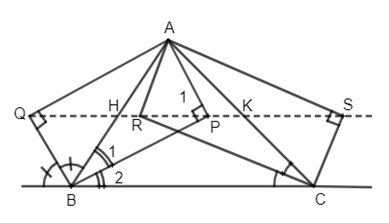
a) Ta có BQ và BP là hai phân giác của hai góc kề bù nên \(\widehat {QBP} = {90^ \circ }\) lại có \(\widehat {AQB} = \widehat {APB} = {90^ \circ }\left( {gt} \right)\)
Do đó tứ giác APBQ là hình chữ nhật (có ba góc vuông).
b) Chứng minh tương tự ta có tứ giác ASCR là hình chữ nhật nên PQ đi qua trung điểm H của AB. Tương tự RS cũng đi qua trung điểm K của AC. Lại có \(HK// BC\left( 1 \right)\)
Mặt khác ta có \(\widehat {{P_1}} = \widehat {{B_1}}\) (tính chất hai đường chéo hình chữ nhật) mà \(\widehat {{B_1}} = \widehat {{B_2}}\left( {gt} \right)\) \(\widehat {{P_1}} = \widehat {{B_2}} \Rightarrow HP//BC\) (2)
Từ (1) và (2) HK và HP phải trùng nhau hay ba điểm H, P, K thẳng hàng, mà Q, H, P cũng thẳng hàng
\(\Rightarrow \) bốn điểm Q, H, P, K thẳng hàng.
Chứng minh tương tự: \(HR//BC \Rightarrow S,K,R,H\) thẳng hàng.
dapandethi.vn
