Chọn đáp án đúng:
6.37
Cho 0 < α < π/2. Biểu thức \(S = \dfrac{{\sin 4\alpha - 2\sin 2\alpha }}{{\sin 4\alpha + 2\sin 2\alpha }}\) có thể rút gọn thành biểu thức nào sau đây?
A. -tan2α B. tanα
C. cot2α D. cotα
Lời giải chi tiết:
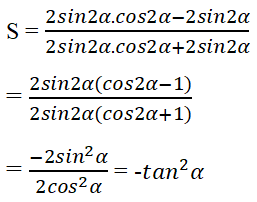
Đáp án: A
Ta cũng có thể suy luận cos2α – 1 < 0, cos2α + 1 > 0 nên S < 0, do đó các phương án B, C, D bị loại. Vậy đáp án là A.
6.38
Cho tan2a = 4/3 với π/2 < a < π. Giá trị cos a là

Lời giải chi tiết:
Cách 1. Tính trực tiếp:

Vì π/2 < a < π nên tan a < 0, do đó tan a = -2.
Áp dụng công thức
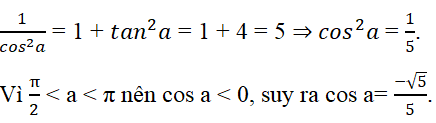
Đáp án là B.
Cách 2. Suy luận
Vì π/2 < a < π nên cos a < 0, do đó các phương án A, C, D bị loại.
Đáp án: B
6.39
Biết sin2a = -4/5 với 3π/4 < a < π. Giá trị tan a là
A. 1/2 B. 2
C. -2 D. -1/2
Lời giải chi tiết:
Cách 1. Tính trực tiếp.

Vì 3π/4 < a < π nên tan a < 0. Vậy tan a = (-1)/2. Đáp án là D.
Cách 2. Suy luận
Với 3π/4 < a < π thì -1 < tan a < 0, nên các phương án A, B, C đều bị loại.
Đáp án: D
6.40
Cho tanα = 2cotα và 3π/2 < α < 2π. Giá trị của biểu thức sinα + cosα là

Lời giải chi tiết:
Cách 1. Tính trực tiếp
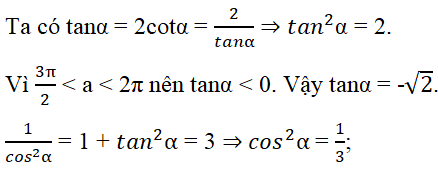
Do đó cosα = √3/3 (vì cosα > 0).
Suy ra sinα = tanα.cosα = (-√6)/3.
Vậy sinα + cosα = (√3- √6)/3. Đáp án là B.
Cách 2. Suy luận
Vì tanα = 2cotα và 3π/2 < α < 2π nên 3π/2 < α < 7π/4.
Do đó sinα < (-√2)/2 và cosα < √2/2.
Vì vậy sinα + cosα < 0.
Suy ra các phương án A, C, D bị loại.
Đáp án: B
6.41
Biết sinα - cosα = 1/2 và π < α < 5π/4. Giá trị cot2α là

Lời giải chi tiết:
Cách 1. Tính trực tiếp
Ta có (sinα – cosα)2 = 1/4 = 1 – sin2α ⇒ sin2α = 3/4.
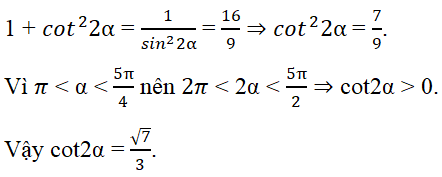
Đáp án là D.
Cách 2. Suy luận
Vì π < α < 5π/4 nên 2π < 2α < 5π/2. Suy ra cot2α > 0. Do đó các phương án A, B, C đều bị loại.
Đáp án: D
dapandethi.vn
