Đề bài
Một đường thẳng đi qua tiêu điểm \(F(c ; 0)\) của elip \((E): \dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\) \((a>b>0)\) và cắt nó tại hai điểm \(A, B\). Chứng minh rằng đường tròn đường kính \(AB\) không có điểm chung với đường chuẩn :\(x = \dfrac{a}{e}\).
Lời giải chi tiết
(h.126).
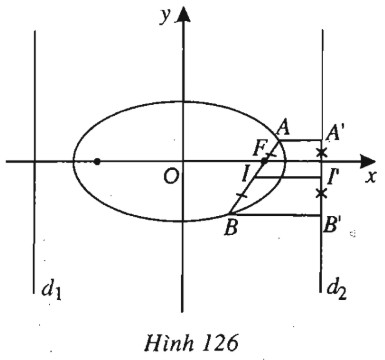
Gọi \(I\) là trung điểm của \(AB; A’, B’, I’\) lần lượt là hình chiếu của \(A, B, I\) trên đường chuẩn \({d_2}: x = \dfrac{{{a^2}}}{c}\).
Ta sẽ chứng minh:
\(II' > \dfrac{{AB}}{2} \Leftrightarrow AA' + BB' > AB\).
Ta có
\(AB = AF + BF = e.AA' + e.BB' \)
\(= e(AA' + BB') < AA' + BB' = 2II'\) (do \(e<1\)). Suy ra điều cần chứng minh.
dapandethi.vn
