Câu 1
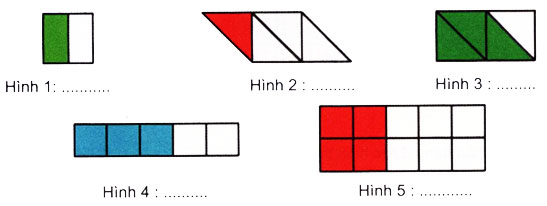
Viết phân số biểu thị phần đã được tô màu trong mỗi hình sau:
Phương pháp giải:
- Quan sát hình vẽ để viết phân số tương ứng với mỗi hình.
- Trong mỗi phân số, tử số chỉ số phần bằng nhau đã được tô màu và mẫu số chỉ tổng số phần bằng nhau.
Lời giải chi tiết:
Hình 1 được chia thành 2 phần bằng nhau, trong đó có 1 phần được tô màu. Do đó phân số biểu thị phần đã được tô màu trong hình 1 là : \(\dfrac{1}{2}\).
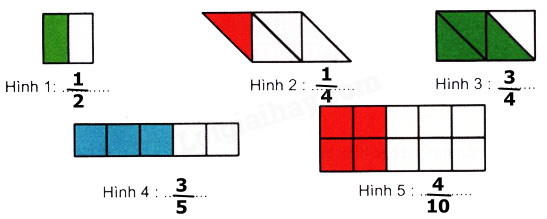
Tương tự cách làm như vậy ta có kết quả như sau :
Câu 2
a) Điền dấu thích hợp \(<, =, >\) vào chỗ chấm :
\(\dfrac{5}{4}\,\,...\,\,\dfrac{3}{4}\,\,;\) \(\dfrac{3}{4}\,\,...\,\,1\,\,;\) \(\dfrac{2}{3}\,\,...\,\,\dfrac{4}{7}.\)
b) Viết các phân số: \(\dfrac{3}{2};\,\dfrac{2}{8};\,\dfrac{5}{6};\,\dfrac{3}{4}\) theo thứ tự từ lớn đến bé.
Phương pháp giải:
a) Áp dụng các quy tắc :
- Trong hai phân số có cùng mẫu số, phân số nào có tử số lớn hơn thì lớn hơn.
- Phân số có tử số bé hơn mẫu số thì bé hơn 1.
- Muốn so sánh hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số rồi so sánh hai phân số sau khi quy đồng.
b) So sánh các phân số đã cho rồi sắp xếp theo thứ tự từ lớn đến bé.
Lời giải chi tiết:
a) • \(\dfrac{5}{4} > \dfrac{3}{4}\) (vì \(5 > 3\)).
• \(\dfrac{3}{4} < 1\) (vì \(3 < 4\)).
• \(\dfrac{2}{3} > \dfrac{4}{7}\)
Giải thích : Ta có :
\(\dfrac{2}{3} = \dfrac{{2 \times 7}}{{3 \times 7}} = \dfrac{{14}}{{21}}\,\,;\) \(\dfrac{4}{7} = \dfrac{{4 \times 3}}{{7 \times 3}} = \dfrac{{12}}{{21}}.\)
Mà \(\dfrac{{14}}{{21}} > \dfrac{{12}}{{21}}\) (vì \(14 > 12\)).
Vậy \(\dfrac{2}{3} > \dfrac{4}{7}.\)
b) Ta có :
• \(\dfrac{3}{2} = \dfrac{{3 \times 12}}{{2 \times 12}} = \dfrac{{36}}{{24}}\,\,;\) • \(\dfrac{2}{8} = \dfrac{{2 \times 3}}{{8 \times 3}} = \dfrac{6}{{24}}\,\,;\)
• \(\dfrac{5}{6} = \dfrac{{5 \times 4}}{{6 \times 4}} = \dfrac{{20}}{{24}}\,\,;\) • \(\dfrac{3}{4} = \dfrac{{3 \times 6}}{{4 \times 6}} = \dfrac{{18}}{{24}}.\)
Mà \(\dfrac{{36}}{{24}} > \dfrac{{20}}{{24}} > \dfrac{{18}}{{24}} > \dfrac{6}{{24}}\) (vì \(36 > 20 > 18 > 6\)).
Hay \(\dfrac{3}{2} > \dfrac{5}{6} > \,\dfrac{3}{4} > \,\dfrac{2}{8}.\)
Vậy các phân số đã cho được viết theo thứ tự từ lớn đến bé là \(\dfrac{3}{2};\,\dfrac{5}{6};\,\dfrac{3}{4};\,\dfrac{2}{8}\).
Câu 3
Khoanh vào chữ đặt trước câu trả lời đúng:
Phân số \(\dfrac{5}{6}\) bằng phân số nào dưới đây:
A. \(\dfrac{{50}}{{60}}\) B. \(\dfrac{{20}}{{18}}\) C. \(\dfrac{{15}}{{24}}\) D. \(\dfrac{{20}}{{30}}\)
Phương pháp giải:
Áp dụng tính chất cơ bản của phân số : Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
Ta có : \(\dfrac{5}{6} = \dfrac{{5 \times 10}}{{6 \times 10}} = \dfrac{{50}}{{60}}\)
Vậy phân số \(\dfrac{5}{6}\) bằng phân số \(\dfrac{{50}}{{60}}\).
Chọn đáp án : A. \(\dfrac{{50}}{{60}}\).
Câu 4
Tính:
\(a)\,\,\dfrac{3}{5} + \dfrac{5}{8}\,\,;\) \(b)\,\,\dfrac{{21}}{{40}} - \dfrac{3}{8}\,\,;\)
\(c)\,\,\dfrac{5}{7} \times \dfrac{{12}}{{11}}\,\,;\) \(d)\,\,\dfrac{{15}}{7}:\dfrac{5}{{14}}.\)
Phương pháp giải:
Áp dụng các quy tắc :
- Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng (hoặc trừ) hai phân số đó.
- Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
- Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Lời giải chi tiết:
\(a)\,\,\dfrac{3}{5} + \dfrac{5}{8} = \dfrac{{24}}{{40}} + \dfrac{{25}}{{40}} = \dfrac{{49}}{{40}}\,\,;\)
\(b)\,\,\dfrac{{21}}{{40}} - \dfrac{3}{8} = \dfrac{{21}}{{40}} - \dfrac{{15}}{{40}} = \dfrac{6}{{40}} = \dfrac{3}{{20}}\,\,;\)
\(c)\,\,\dfrac{5}{7} \times \dfrac{{12}}{{11}} = \dfrac{{5 \times 12}}{{7 \times 11}} = \dfrac{{60}}{{77}}\,\,;\)
\(d)\,\,\dfrac{{15}}{7}:\dfrac{5}{{14}} = \dfrac{{15}}{7} \times \dfrac{{14}}{5} = \dfrac{{15 \times 14}}{{7 \times 5}}\)\( = \dfrac{{5 \times 3 \times 7 \times 2}}{{7 \times 5}} = 6.\)
Câu 5
Tính diện tích của mỗi hình theo số đo dưới hình vẽ :
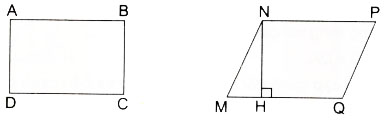
AB = 6cm, BC= 4cm MQ= 6cm, NH = \(\dfrac{2}{3}\) MQ
Phương pháp giải:
Áp dụng các quy tắc :
- Muốn tính diện tích hình chữ nhật ta lấy chiều dài nhân với chiều rộng (cùng một đơn vị đo).
- Muốn tính diện tích hình bình hành ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo).
Lời giải chi tiết:
a) Diện tích hình chữ nhật ABCD là :
6 × 4 = 24 (cm2)
b) Chiều dài cạnh NH là :
6 × \(\dfrac{2}{3}\) = 4 (cm)
Diện tích hình bình hành MNPQ là :
6 × 4 = 24 (cm2)
Câu 6
Giải bài toán sau:
Biết lớp 4A có 35 học sinh. Số học sinh nam bằng \(\dfrac{2}{5}\) số học sinh của lớp. Tính số học sinh nam và học sinh nữ của lớp 4A.
Phương pháp giải:
- Tính số học sinh nam ta lấy số học sinh cả lớp nhân với \(\dfrac{2}{5}\).
- Tính số học sinh nữ ta lấy số học sinh cả lớp trừ đi số học sinh nam.
Lời giải chi tiết:
Tóm tắt
Lớp 4A: 35 học sinh
Học sinh nam: \(\dfrac{2}{5}\) số học sinh của lớp
Học sinh nam: .... bạn?
Học sinh nữ: .... bạn?
Bài giải
Lớp 4A có số học sinh nam là :
\(35 \times \dfrac{2}{5} = 14\) (học sinh)
Lớp 4A có số học sinh nữ là :
\(35 - 14 = 21\) (học sinh)
Đáp số: Nam : \(14\) học sinh ;
Nữ : \(21\) học sinh.
dapandethi.vn
